|
In dit deel van het avontuur voert Einstein ons langs een
paar vervaarlijke wiskundige obstakels. Schijnbaar spelenderwijs leidt hij
wiskundige formules af waarmee hij tijd en plaats in een bewegend stelsel
berekent, maar wij dreigen ons lelijk te stoten en we verliezen het houvast.
Helmen op! De balken komen in beweging. Er worden afstanden afgelegd. De tijd
lijkt ongrijpbaar. We vinden echter een hangbrug voor de omrekening van het ene
stelsel naar het andere. Iedere plaats en ieder tijdstip in het stelsel–in–rust
wordt verbonden met een plaats en een tijd in het bewegende stelsel. Het geheim
zit in de transformatieformules.
Denk niet dat we de tocht in korte broek en op sandalen
aankunnen. Een goede voorbereiding wordt gevraagd. Een degelijke uitrusting is
vereist.
Waar gaat het om? Wat is zo’n omrekening?
Een voorbeeld: je weet dat als we in een rijdende trein een
euro recht omhooggooien we de munt weer op dezelfde plaats kunnen opvangen. Je
hoeft je hand nauwelijks te bewegen. De munt gaat recht omhoog en valt weer
recht naar beneden op je hand en als je goed oplet, zie je dat de munt onderweg
naar boven steeds langzamer beweegt en naar beneden steeds sneller valt: daar
zit de zwaartekracht achter. Ondertussen reizen we mee in het stelsel dat door
de rijdende trein wordt gevormd, maar dat schijnt geen invloed te hebben op de
beweging van de munt.
Als we buiten op een grasveld op dezelfde manier een euro
recht omhooggooien, beweegt hij ook vertraagd omhoog om daarna versneld naar
beneden te vallen. De beweging is precies hetzelfde.
Maar als we nu vanaf het gras naar een passerende trein
kijken, waarin we iemand zien die een euro opgooit, dan is de trein al een heel
eind verderop tegen de tijd dat de munt wordt opgevangen. Het muntstuk is dus
geenszins recht omhoog gegaan en vervolgens weer recht naar beneden gevallen,
beslist niet! Iedere boerenpummel (zeker als hij in militaire dienst is geweest)
weet dat de munt een kogelbaan heeft beschreven en met een kogelbaan wordt een
parabolische baan bedoeld.

Figuur 3.01 Een kogelbaan
De passagier in de trein en wij op het gras bekijken
hetzelfde verschijnsel. Toch doorloopt het muntje twee zeer verschillende banen:
de passagier ziet een verticale rechte lijn en wij zien een kogelbaan . Omdat
het uiteindelijk om dezelfde beweging van hetzelfde muntje gaat, moet de
beschrijving van de passagier "vertaald" kunnen worden in de
beschrijving die wij er aan geven en omgekeerd. Dat wordt de omrekening genoemd,
de transformatie.
Hoe rekenen we de kogelbaan om naar dat rechte op en neer
gaande lijntje dat de passagier ziet. Dat is de kunst. Het uitgangspunt is dat
zowel in de trein als buiten in het gras dezelfde wet geldt, namelijk dat als je
een voorwerp recht omhoog gooit dit voorwerp volgens de wet van Newton weer
recht naar beneden valt omdat er maar één kracht op wordt uitgeoefend, de
zwaartekracht. De natuurkunde is in de trein dezelfde als op het gras. Het
voorwerp moet rechtlijnig bewegen met een versnelling in neerwaartse richting.
In welk stelsel we ons bevinden, doet er niet toe: altijd een recht lijntje.
Maar als je het rechte lijntje in de trein bekijkt vanaf het gras, is het een
kogelbaan, dus vanuit wélk stelsel je het verschijnsel bekijkt, doet wél
terzake!
De omrekening werd al door Galileo Galileï bedacht en
toegepast. De oude wijsgeer had ook als eerste doorzien dat een voorwerp waarop
geen enkele kracht wordt uitgeoefend, zich eenparig rechtlijnig voortbeweegt.
Wij gaan zijn omrekeningsmethode gebruiken in combinatie met de
bewegingsvergelijkingen die we te danken hebben aan Isaäc Newton .
We bekijken eerst welke formules er voor de beweging van een
muntje gelden als we het stilstaand in het gras recht omhooggooien. Daarna
onderzoeken we welke formules we op kunnen stellen die de beweging, zoals wij
die waarnemen, beschrijven van het muntje dat door de passagier wordt
opgeworpen. Tenslotte laten we zien dat we met de juiste omrekeningsformules de
passagier aan een stel formules kunnen helpen die voor hem de beweging van het
muntje op de juiste wijze beschrijven.
Hoe beschrijven we de beweging van het muntje dat door een
stilstaand persoon langs de spoorbaan recht omhoog wordt gegooid? Daarvoor
gebruiken we een assenstelsel: de x-as horizontaal langs de spoorbaan
gericht, de y-as verticaal loodrecht op de x-as en de z-as naar
ons gericht, zie fig. 3.02. Zo’n loodrecht stelsel wordt een cartesisch
assenstelsel genoemd. In de vorige paragraaf (§2plus) hebben we er al
ruimschoots gebruik van gemaakt.
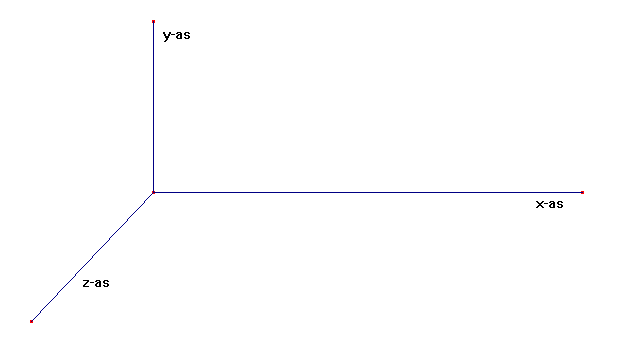
Figuur 3.02 Een cartesisch assenstelsel
De plaats van de munt in verticale richting wordt gegeven
door
y(t) = y(0) + vy .t – ½ .g .t²
waarbij y(0) de hoogte is waarop de munt zich bevindt
op het tijdstip t = 0 (vul voor t maar eens 0 in,
dan zie je dat de twee laatste termen 0 worden, dus wegvallen),
vy is de verticale snelheid omhoog die het
voorwerp op het tijdstip t = 0 meekrijgt
en g is de versnelling van de zwaartekracht, waarvoor
de afgeronde waarde g = 9,8 m/s2 geldt.
Voor de laatste term ½ .g . t² staat een minteken
omdat de versnelling naar beneden is gericht. De snelheid en de versnelling
worden positief gerekend als ze omhoog gericht zijn.
(We laten verder alle krachten, die voor het proefje niet van
belang zijn, buiten beschouwing).
Voorbeeld:
Als we de munt, stilstaand langs de spoorbaan, opgooien op
een hoogte van 1 meter, dat wil zeggen: de munt verlaat onze hand op het
tijdstip t = 0 op een hoogte van 1 meter, dan is y(0) = 1 m.
We geven het muntje een snelheid van vy = + 3 m/s mee. Dat
lijkt veel, want u denkt dat de proef dan niet in de trein herhaald kan worden
omdat de munt tegen het plafond aanvliegt. We zullen zien dat dat meevalt, de
zwaartekracht haalt in de kortste keren de snelheid uit de munt en trekt hem
weer naar beneden.
De coördinaten van het bewegende muntje kunnen we, als we de
proef uitvoeren terwijl we zelf met onze voeten in het nulpunt van het stelsel
gaan staan, op de volgende manier als functie van de tijd geven:
x(t) = 0 (in de x–richting verandert de
euro niet van plaats, dat wil zeggen de munt verplaatst zich niet met de
trein mee of er tegenin)
y(t) = 1 + 3.t – ½ . 9,8 .t2 meter (de
bewegingsvergelijking in de y-richting)
z(t) = 0 (voor de z–richting geldt hetzelfde als
voor de x-richting)
Samengevat in de "formules bij stilstand":
x(t) = 0
y(t) = 1 + 3.t – ½ . 9,8 .t2
"formules
bij stilstand"
z(t) = 0
We berekenen eerst na hoeveel tijd het muntje weer terug is
in onze hand. Zijn hoogte is dan weer 1 meter. Dus y(t) = y(0) = 1 m.
Ingevuld in de formule:
y(t) = y(0) + vy.t – ½ .g .t² → y(t) =
y(0) + 3.t – ½ . 9,8 .t2 → 1 = 1 + 3.t – ½ . 9,8 .t2
De beginhoogte (= 1 m) valt tegen de eindhoogte (=
1 m) weg en we krijgen:
0 = 3.t – ½ . 9,8 .t2 = als we t buiten haakjes
brengen = (3 – ½ . 9,8 .t) . t
De laatste uitdrukking is dus gelijk aan nul. Als we deze
vergelijking oplossen verkrijgen we de tijdstippen t waarbij y(t)
gelijk is aan 1 meter, dat zijn de momenten waarop de munt onze hand
verliet en weer terugkwam op onze hand. Oplossen betekent dus dat je de
tijdstippen t vind waarbij de laatste uitdrukking nul wordt, want op
die tijdstippen heeft het muntje de hoogte van 1 meter.
De uitdrukking wordt nul als:
t = 0 (dat was het moment dat we het muntje opgooiden)
of
3 – ½ . 9,8 .t = 0 Als je dat uitrekent, komt er
uit: t = 3/4,9 = 0,612 seconde.
Dus na 0,612 s is het muntje terug.
Vervolgens berekenen we op welk tijdstip de munt zijn hoogste
punt had bereikt. Dat is niet moeilijk want het muntje beweegt even lang naar
boven als naar beneden. De zaak is symmetrisch, dus na t = 0,612 / 2 = 0,306
seconde wordt de top bereikt.
Hoe hoog komt het muntje dan?
Daartoe vullen we alle bekende waarden in de formule y(t)
= y(0) + vy.t – ½ .g .t² in , dus
y(0,306) = 1 + 3 . 0,306 – ½ . 9,8 .0,3062 =
1,459 meter. Dit is de gevraagde hoogte.
 |
Oefening 8
Bereken hoe hoog het muntje zou zijn gekomen als het een beginsnelheid van 5
m/s had meegekregen vanaf een hoogte van 50 cm.
|
Vervolgens kijken we op een afstand van 30 meter van
het midden van de rails naar de passerende trein, waar iemand op het middenpad
ook een euro opgooit op 1 meter hoogte met een verticale beginsnelheid
van + 3 m/s . De passagier bevindt zich hoger dan de toeschouwer in het
gras omdat de vloer van de trein zich op 1,25 m hoogte bevindt. Voor de
toeschouwer is de beginhoogte van de munt 2,25 m. De munt wordt
tegelijkertijd met de trein in horizontale richting meegevoerd. De verticale
baan voor de passagier in de trein wordt voor de toeschouwer uitgerekt in
horizontale richting en hij ziet een kogelbaan.
De plaats van het muntje (gezien vanaf het gras) in
horizontale richting, langs de x-as, kunnen we beschrijven vanaf het
moment (t = 0) dat het werd opgegooid, met
x(t) = x(0) + vx . t
met vx = de horizontale snelheid van de
trein, dat is gewoon de verplaatsing van de trein waarin die vent met dat muntje
zich bevindt. Hierin is x(0) de plek (gezien vanaf het gras) waar de man
zich bevond op het moment dat het muntje zijn kortstondige verticale reisje
begon. Voor het gemak geven we die plek de waarde x(0) = 0 meter.
Als we eens aannemen dat de trein met een matige snelheid van
25 m/s (= 90 km/uur) passeert, dan is het muntje tijdens het opgooien
(wat 0,612 s duurde) over een afstand van
vx . t = 25 .0,612 = 15,3 meter in
horizontale richting meegevoerd.

Fig. 3.03 Trein met baan van de munt
|
|
Voor de toeschouwer op het gras bestaat de beweging van het
muntje van de passagier uit twee delen:
 |
Een verticale beweging net zo als
zijn eigen muntje had gemaakt, maar dan met een beginhoogte van 2,25 m. |
 |
Een horizontale beweging die gelijk
opgaat met de snelheid van de trein en die bij zijn eigen muntje geheel
ontbrak (gelukkig maar, anders was hij zijn muntje kwijt geweest). |
De toeschouwer stelt zich nu ten doel de onwetende passagier
aan een formule te helpen opdat de laatste de beweging van het muntje dat hij in
de trein opgooit, kan beschrijven.
De toeschouwer kan de beweging die hij ziet in drie formules
weergeven. Voor de beweging langs de x–richting de net genoemde
formule:
x(t) = x(0) + vx . t , waarin x(0) = 0
meter en vx = 25 m/s .
Voor de beweging langs de y–richting, de verticale
richting:
y(t) = y(0) + vy.t – ½ .g .t² met y(0)
= 2,25 meter en vy = 3 m/s en g = 9,8 m/s2 .
In de z–richting de afstand van de toeschouwer tot
de rails waarlangs de trein en het muntje bewegen:
z(t) = z(0) met z(0) = – 30 meter. Die afstand
blijft constant.
Samengevat in de drie "toeschouwerformules":
x(t) = + 25 . t
y(t) = 2,25 + 3 . t – ½ . 9,8 . t²
"toeschouwerformules"
z(t) = – 30 m
Als je van deze formules uitgaat, moet de redenatie van de
toeschouwer nu de volgende zijn:
De passagier kiest natuurlijk een assenstelsel dat met hem
meebeweegt en waarbij hij met zijn voeten in de oorsprong staat.
Van de beweging in de x–richting, de richting waarin de trein zich
beweegt, trek ik dan de verplaatsing van de trein er af, want de passagier staat
stil in de trein.
Tenslotte haal ik in de y–richting, de vloerhoogte van 1,25 meter
er af omdat de passagier zich 1,25 meter hoger bevindt dan ik. Voor hem
is het muntje minder hoog dan voor mij.
Bij de plaats in de z–richting tel ik die 30 meter er bij op omdat de
passagier in de trein zich in de oorsprong van zijn stelsel bevindt .
De toeschouwer verkrijgt de volgende formules, waarbij hij
voor de x, y en z–coördinaat van de passagier de symbolen ξ,
η en ζ
gebruikt .
 |
ξ (t) = x(t) – 25 . t meter |
 |
η(t) = y(t) – 1,25 meter |
 |
ζ(t) = z(t) + 30 meter |
Dit zijn de omrekeningsformules.
 |
Het is een vervelend, maar niet te
vermijden gebruik in de wetenschap en de techniek om zich te bedienen
van symbolen, vaak Griekse letters en vaak wordt hetzelfde symbool ook
nog eens voor verschillende begrippen gebruikt. Dat is verwarrend,
akkoord, maar je kan het wel aan. De hier gebruikte Griekse letters
hebben de volgende namen: ξ
heet xi; η heet ètha en ζ
heet dzèta, wat betreft de klank gelijkend op de x, y en z. |
Als we de "toeschouwerformules" invullen,
met de concrete waarden die erbij gegeven zijn, krijgen we:
ξ (t) = +25.t – 25.t = 0 meter
η(t) = 2,25 + 3.t – ½ .9, 8 .t²
– 1,25 = 1 + 3.t – ½ .9,8 .t² meter
ζ(t) = –30 + 30 = 0 meter
Samengevat :
 |
ξ(t) = 0 |
 |
η(t) = 1 + 3 .t – ½ .9,8 .t² |
 |
ζ (t) = 0 |
Deze formules zien er net zo uit als de "formules
bij stilstand". Ze hebben dezelfde vorm. Dat is ook de bedoeling, want
de passagier ziet precies zo’n beweging in verticale richting als de
toeschouwer in het gras die zijn muntje recht omhoog gooide: we hebben het
goed omgerekend.
Je kan de omrekening ook de andere kant op maken. Dan ziet de
passagier de toeschouwer in het gras met een snelheid van – 25 m/s
achterblijven, op een hoogte van – 1,25 meter ten opzichte van
zijn nulpunt (zijn voeten) en op een loodrechte afstand van + 30 meter.
Als hij van zijn eigen formules uitgaat, zal hij uiteindelijk de "formules
bij stilstand" vinden.
Dit voorbeeld geeft aan wat bedoeld wordt met een omrekening
van het ene stelsel naar het andere stelsel. Deze manier van omrekenen wordt de
Galileïtransformatie genoemd. Omdat deze omrekeningsmethode zo overtuigend
is, ging men er argeloos vanuit dat daar niets mis mee kon zijn tot de
wetenschap vastliep in zijn pogingen om de beweging van de aarde in de
lichtether aan de tonen. Iedereen zat met zijn handen in het haar, wat aan
Einstein jaren later nog te zien was, maar hij maakte een onverwachte
geestelijke reuzenzwaai door te concluderen dat onze omrekeningsformules niet
klopten. Dat kwam hard aan in de wetenschap, die er echter hard aan toe was.
Na deze voorbereiding gaan we weer op pad. Wees alert op de
valkuilen en draaikolken waar Einstein ons langs zal voeren. Doe het rustig aan.
Zij met ervaring mogen af en toe een stukje voor de rest uit, de anderen zullen
op dit glibberige pad vaak moeten wachten op een helpende hand. Onderweg vinden
we rustplaatsen waar we op elkaar zullen wachten. Dat spreken we af!
De bewegende balk wordt vervangen door een bewegend
coördinatenstelsel (zie figuur 304). Het stelsel–in–rust krijgt het
symbool K en het stelsel–in–beweging krijgt het symbool k
. Stelsel k beweegt met de snelheid v naar rechts.
De assen blijven ondanks de snelheid v loodrecht op elkaar staan
en parallel aan de assen van stelsel K. "Uit
symmetrieoverwegingen", zoals Einstein zegt. Wat zit daarachter, wat
bedoelt hij daarmee?
Daar zit een scherpe, logische redenering achter. Let op: De
plaats en de richting van het stelsel K zijn willekeurig gekozen in de
ruimte. De y– en z–as van K staan loodrecht op de x–as. Als de
overeenkomstige assen van het stelsel k , dat met de snelheid v in
de richting van de positieve x–as van het stelsel K beweegt,
achterover, in de richting van de negatieve x–as zouden hellen, dan volgt er
uit dat die assen, als de snelheid van richting wordt omgedraaid, achterover
naar de positieve x–as zouden moeten hellen. Daar is de natuur consequent in.
Wanneer je vervolgens een nieuw stilstaand stelsel K* introduceert, dat
samenvalt met het eerste K, met dit verschil dat de positieve en de negatieve x–as
verwisseld zijn, dan krijg je de situatie dat de assen van het bewegende stelsel
gelijktijdig achterover (in stelsel K) en voorover (in K*) moeten
hellen. Dat is in strijd met elkaar. Dat kan dus niet. De assen van k
moeten loodrecht op de x–as blijven staan.
Zo simpel is dat.

Fig. 3.04 Het stelsel–in–rust K en het stelsel–in–beweging
k
In ieder stelsel kunnen afstanden worden gemeten met
onvervormbare meetstaven en tijden met onderling gelijklopende klokken. In het
stelsel K wordt de plaats van een "gebeurtenis" aangegeven met
de coördinaten (x, y, z ) . Het is een punt in de ruimte, maar
bij dat punt hoort ook een tijdstip t van het waarnemen van het punt.
Samen noemen we dat een "gebeurtenis". De waarde van x, de
waarde van y, de waarde van z en de waarde van t kunnen
worden samengevat als ( x , y , z , t ). Dit noemen we de coördinaten
van een "puntgebeurtenis" in K.
De "puntgebeurtenis" in het stelsel K
vinden we ook terug in het stelsel–in–beweging k (zie fig.305),
want ieder coördinatenstelsel strekt zich over de gehele ruimte en alle tijd
uit. In het stelsel k krijgt de puntgebeurtenis de plaats– en
tijdaanduidingen ξ , η, ζ
en τ . De "punt–gebeurtenis"
krijgt in dit stelsel dus de coördinaten: (ξ
, η, ζ , τ ). Er moet dus een relatie zijn tussen ( x,
y, z, t ) en (ξ , η, ζ ,
τ ). Niet de voor de handliggende relatie zoals de
Galileïtransformatie, maar één waarbij het merkwaardige gedrag van de
ongelijklopende klokken en de te korte balk tot uiting komt.
Hoe zijn de coördinaten van het ene stelsel met die van het
andere stelsel verstrengeld?
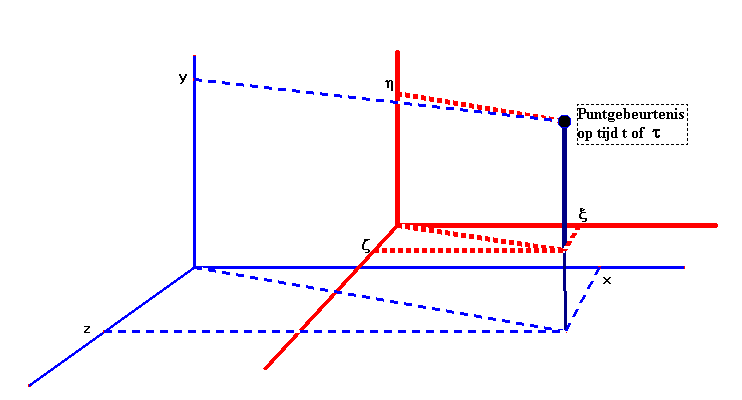
Figuur 3.05 Een "punt–gebeurtenis" P in twee
stelsels waarvan de assen niet samenvallen
Om te beginnen, stelt Einstein, moeten de vergelijkingen lineair
zijn omdat we ruimte en tijd als homogene grootheden zien.
Even een stukje toelichting.
Met homogeen wordt bedoeld dat afstand en tijd in de
gehele ruimte gelijkmatig zijn verdeeld. Er zijn dus geen gebieden waar alles
vlugger of langzamer gaat en er zijn geen gebieden waar alles kleiner of groter
is. Overigens zou dat moeilijk te constateren zijn als je er zelf deel van
uitmaakt en de veranderingen geleidelijk zouden verlopen. Het is dus een
veronderstelling. Hoe het ook zij, in onze ervaring heeft niets de laatste eeuw
op het tegendeel gewezen terwijl we toch een behoorlijke afstand door de ruimte
en in de tijd hebben afgelegd. De komende afleiding is dus geldig voor ruimte en
tijd die gelijkmatig zijn verdeeld.
 |
Een beetje wantrouwen is op zijn plaats want we hebben al
gezien dat afstand en tijd in een bewegend stelsel vreemd doen en met onze
huidige kennis weten we ook dat nabij (zware) massa’s de tijd en de ruimte
beslist niet homogeen zijn. |
Het homogeen zijn betekent tevens dat als de tijd in het
stelsel–in–beweging op een bepaald punt sneller of langzamer is dan de tijd
in het stelsel–in–rust dat de tijd dan in het eerste stelsel overal in
dezelfde mate sneller of langzamer moet zijn ten opzichte van het stelsel–in–rust,
want dan alleen blijft de homogeniteit behouden. Hetzelfde geldt voor de ruimte.
Maar voor dergelijke uniforme vergrotingen of verkleiningen heb je lineaire
vergelijkingen nodig. Die zorgen voor een gelijkmatige omrekening van het ene
stelsel naar het andere stelsel.
Een lineaire vergelijking; wat was dat ook weer?
De algemene vorm kan je schrijven als y = a.x + b .
Als je dit in een grafiek weergeeft, verkrijg je een rechte lijn. De richtingscoëfficiënt
van de lijn is het getal a, waarmee wordt aangegeven hoeveel y
verandert als x met het getal één toeneemt. Het getal b geeft
het snijpunt met de x-as. Voorbeeld: y = 0,5 . x + 1 (zie fig.3.06).
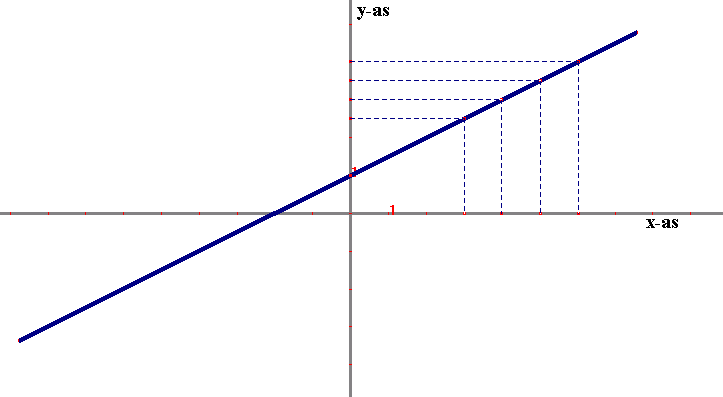
Fig. 3.06 Een lineaire functie
In de figuur is de functie y = 0,5 . x + 1 weergegeven.
Bij iedere waarde van x hoort een waarde van y . Als je van een x–waarde
uitgaat, trek je een verticaal lijntje tot je de schuine lijn snijdt en
daarvandaan trek je een lijn in horizontale richting tot je de y–as
snijdt. Het laatste snijpunt is de y–waarde die bij de x–waarde
hoort. Wanneer je dit doet voor verschillende x–waarden die op gelijke
afstanden van elkaar liggen, dan vind je y–waarden die ook op gelijke
afstanden van elkaar liggen. In ons plaatje liggen de y–waarden dichter
bijeen dan de x–waarden. Hier heb je te maken met een verkleining en
die geldt overal, waar je de x–waarden ook kiest: de bijbehorende y–waarden
liggen dichter bij elkaar.
Wanneer de schuine lijn onder een hoek van 45 º loopt, zijn
de afstanden op beide assen gelijk en als de functie steiler loopt, liggen de y–waarden
verder uiteen en kan je over een vergroting spreken. In ieder geval blijft de
homogeniteit behouden!
Nu vlug terug naar Einstein want hij wil iets vertellen.
"Probeer je eens een stilstaand punt x′ in
stelsel k voor te stellen", oppert hij.
Figuur 3.07 Hier heeft x′ een vaste plaats in
stelsel k , maar het beweegt in stelsel K.
 |
Je moet dus in gedachten meekijken met het stelsel
k
waarin x′ stilstaat. Welke waarde x′ heeft doet er
helemaal niet toe. |
Omdat het stelsel k met een snelheid v langs de
x-as van het stelsel–in–rust K beweegt, geldt voor de x–waarde
van dit punt in stelsel K, als je de blik op stelsel K gericht
houdt:
x = v . t + x′
 |
Deze formule geldt als je de twee oorsprongen op
t = 0
laat samenvallen. Op t = 0 geldt dan x = x′. |
Uit x = v . t + x′ volgt:
x′ = x
– v . t .
Omdat x′ constant is, het is een stilstaand punt in
het stelsel k, kan de waarde x′ niet afhankelijk van de tijd
zijn. De term "– v . t " wordt kennelijk gecompenseerd door
de waarde van x . De y–waarde en de z–waarde van dat
punt zijn eveneens constant (gelijk aan 0) omdat het punt geen beweging
vertoont in die richtingen. Het stel coördinaten (x′ , y , z )
is dus onafhankelijk van de tijd. Houd dat in gedachten en knoop het in uw oren!
En nu komt er een stuk wiskunde. Wees niet bang, er kan niets
gebeuren. Het duurt ook niet lang, één bladzijde maar, ….. bij Einstein.
|
Hij wil dat twee klokken in het stelsel–in–beweging
gelijk worden gezet, namelijk een klok die in de oorsprong wordt gezet van het
stelsel–in–beweging en een klok bij het punt x′ . Terwijl onze
trouwe cowboys op de balk al voorbereidingen treffen om via heen en weer gaande
lichtstralen de klokken gelijk te zetten, laat Einstein weten dat we het
probleem theoretisch aanpakken. Er zal worden gedifferentieerd. En niet zo
zuinig. Hij wil ons zeker imponeren.
"Maar moeten wij dat ook kunnen?" vraagt een
teamlid timide.
Niet twijfelen, wij kunnen het ook! Kop op, je krijgt de
nodige aanwijzingen en je komt er wel door. We zullen langs afgronden gaan, we
springen over rotsspleten en af en toe moeten we ons met een touw uit de nesten
helpen. Maar het lukt je!
Eerst moeten we begrijpen dat een gebeurtenis een gebeurtenis
blijft, vanuit welk stelsel je het ook bekijkt. Bijvoorbeeld het terugkaatsen
van een lichtsignaal tegen een spiegeltje. We hebben gezien dat je kunt
discussiëren over het tijdstip en over de afstand, iemand uit het ene
coördinatenstelsel geeft andere waarden aan de plaats en de tijd dan iemand uit
het andere stelsel, maar de gebeurtenis zelf wordt niet betwijfeld.
Van de twee stelsels is op ieder tijdstip precies bekend waar
ze zich ten opzichte van elkaar bevinden. Daarom kunnen de plaats en tijd (= de
coördinaten) van het ene stelsel uitgedrukt worden in de plaats en de tijd van
het andere stelsel. Dat is wat we gaan doen.
De coördinaten in het stelsel–in–rust K zijn x,
y, z en t . De coördinaten ξ
, η , ζ en τ
in het stelsel–in–beweging k zijn, zoals gezegd, uit te drukken in
die van K, met andere woorden: ξ is
een functie van x, y, z en t , maar ook η
is een functie van x, y, z en t , en ζ
is een functie van x, y, z en t , en tenslotte is ook τ
is een functie van x, y, z en t .
We schrijven dit als :
ξ (x, y, z, t )
η (x, y, z, t )
ζ (x, y, z, t )
τ (x, y, z, t )
In plaats van x gaan we x′ gebruiken, dat
een vast punt in het stelsel–in–beweging k was. Dat kan omdat op
ieder tijdstip t precies bekend is welke afstand er tussen x en
x′ zit. Er geldt x = v . t + x′, dus x –
x′ = v . t . Hieruit volgt dat als je de coördinaten in het
stelsel k uit kan drukken in x , y , z en t , dan
kan je ze ook in x′, y , z en t uitdrukken. Eigenlijk
stappen we nu, in gedachten, over op een met k meebewegend stelsel,
waarbij x′ de waarde behoudt die we waarnemen vanuit het
stelsel-in-rúst. Zo bekijken we als het ware van dichtbij hoe de coördinaten
van het ene en het andere stelsel van elkaar verschillen. We gaan nu de volgende
functies onderzoeken:
ξ (x′, y, z, t )
η (x′, y, z, t )
ζ (x′, y, z, t )
τ (x′, y, z, t )
De tijd τ
is het tijdregiem van het bewegende stelsel en welke tijd er heerst wordt
aangegeven door de klokken die daar gelijklopen. De klokken zijn identiek aan de
klokken van het rustende stelsel dus voor iemand in het stelsel–in–beweging
gaan ze even snel als zo’n zelfde klok in het stelsel–in–rust voor iemand
uit het stelsel–in–rust. Ook een muntje valt in het stelsel–in–beweging
even snel op de grond als in het stelsel–in–rust. Maar als iemand vanuit het
stelsel–in–rust naar de klokken van het stelsel–in–beweging kijkt dan
kan hij ze maar niet gelijk zien lopen. Hoe hij ook kijkt. Het is niet te
verteren, maar het is waar. Het muntje valt evenmin op de normale wijze, maar
dat accepteren we sneller omdat we bekend zijn met de kogelbaan van een vallend
muntje in een rijdende trein, dat is zeker geen rechte verticale lijn..
We zullen eerst τ
als functie van x′, y, z, t onderzoeken.
"Zet in het stelsel–in–beweging de klokken gelijk
volgens de bekende procedure en zoek uit hoe de coördinaten van het ene stelsel
samenhangen met die van het andere". Dat is de opdracht van Einstein. Daar
moeten we het mee doen. We staan er helemaal alleen voor. Maar de cowboys hebben er
zin in. Vanuit de oorsprong van het stelsel–in–beweging vuurt cowboy A
op tijdstip τ0 langs
de ξ –as een lichtsignaal naar
x′ af, dat daar op het tijdstip τ1
door cowboy B wordt weerkaatst om op het tijdstip τ2
weer in de oorsprong aan te komen. Als de klokken gelijklopen, moet gelden:
½ (τ0
+ τ2 ) = τ1
Dan doet het lichtsignaal (in het stelsel–in–beweging)
even lang over de heenweg als over de terugweg. Zo zet je klokken gelijk.
Wordt het je allemaal teveel, ga dan
Terug
Einstein springt in zijn artikel als een berggeit over de problemen heen,
maar laten wij het wat rustiger aan doen! Wij zullen de berekening met kleine
tussenstapjes volgen. We bekijken eerst de tijdstippen van vertrek, weerkaatsing
en aankomst van het lichtsignaal gezien vanuit het stelsel–in–rust.
Omdat τ , zoals we hebben
laten zien, een functie is van x′, y , z en t, kunnen we τ
met deze coördinaten beschrijven, dat wil zeggen: zodra we de waarden van x′,
y, z en t kennen, is de waarde van τ
ook bekend. In de vergelijking ½ . (τ0
+ τ2 ) = τ1
is τ0 de tijd die
je krijgt als je de beginwaarden van x′, y , z en t invult, τ1
krijg je door de waarden van x′, y , z en t in te vullen op
de plaats en de tijd van de weerkaatsing en τ2
wordt gevonden door de waarden van x′, y , z en t, in te
vullen voor de plaats en tijd bij terugkomst van het signaal. We zoeken dus de
waarden van x′, y , z en t, op die drie verschillende
momenten.
Om te beginnen noemen we het tijdstip waarop cowboy A de lichtstraal naar
B zendt het tijdstip t. Op de klokken van de cowboys is dat het
tijdstip τ0.
Wat kunnen we over τ0
vertellen?
Voor de oorsprong van het stelsel k geldt x′
= 0. Bedenk dat x′ een vast punt in het stelsel–in–beweging
is. Als je voor dat vaste punt de plaats neemt waar het lichtsignaal vertrekt of
aankomt, de oorsprong, dan geldt voor dat punt: x′ = 0 . Het punt
waar het lichtsignaal wordt weerkaatst, noemen we voor het gemak gewoon x′.
De waarden 0 en x′ zullen we gebruiken, plus de waarden van y
en z die gewoon 0 zijn, omdat het hele gebeuren zich langs de x–as
afspeelt. De tijd bij de start is eenvoudig t , zo hebben we het
begintijdstip genoemd.
De algemene vorm τ (x′,
y, z, t ) kunnen we nu veel preciezer opschrijven voor het
begintijdstip τ0 door
gebruik te maken van de waarden voor x′ = 0, y = 0 en z = 0.
Zo vinden we: τ0
= τ(0,0,0,t).
(1ste
term)
Valt er over τ1
ook iets meer te zeggen?
Bij de weerkaatsing heeft de tijd in ons stelsel de waarde t
+ x′/( c - v) , omdat het licht vanuit het stelsel–in–rust bezien
er x′/(c - v) seconde over doet om van cowboy A naar cowboy B
te gaan. De weerkaatsing vindt plaats in het punt x′, dat is de
waarde op het moment τ1
van de eerste coördinaat. De x en y coördinaat blijven weer
gewoon 0.
Zo mogen we voor τ1
schrijven:  (3de term)
(3de term)
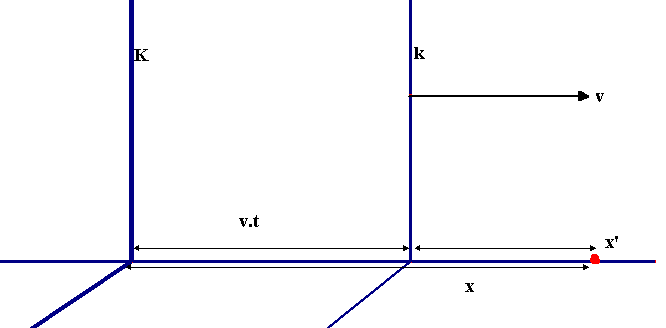
We pakken τ2
op dezelfde manier aan.
Voor de terugweg komt er nog eens x′/(c + v) aan
tijd bij, zodat het tijdstip van terugkomst wordt: t + x′/( c - v) + x′/(c
+ v). De plaats is dan weer gewoon 0 omdat de lichtstraal terugkeert
in de oorsprong.
Zo kan τ2
worden geschreven als 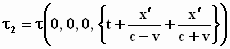 (2de
term)
(2de
term)
Dit zijn de termen op blz. 896 en 897 van
Einsteins artikel.
Wanneer je deze termen invult in de vergelijking voor de
tijden in het stelsel–in–beweging
½ (τ0
+ τ2 ) = τ1
krijg je:
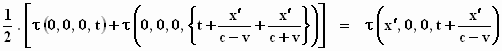
Dit noemen we de
"vervaarlijke vergelijking"
Dat ziet er niet lekker uit en wat kan je ermee? Wat deed
Einstein? Einstein nam gewoon de afgeleide naar x′.
Toe maar! Het moet niet gekker worden!
De afgeleide functie. Zoals je je herinnert had het begrip
veel te maken met de richtingscoëfficiënt, de RC, en het werd ook wel het
differentiequotiënt genoemd. Laten we het even in het kort doornemen. Het mag
niet gebeuren dat één van ons straks zijn grip op de stof verliest en zonder
hulp achter moet blijven!
Als je een functie f hebt van een variabele x,
geschreven als f(x), dan kan je voor twee vlak bijeen gelegen punten x1
en x2 de functiewaarden f(x1) en f(x2)
uitrekenen. We geven met Δx (spreek
uit: delta x) het verschil x2 – x1 aan en
met Δf(x) het verschil f(x2)
– f(x1) . Om de richtingscoëfficiënt te vinden, bereken je:
Maar omdat de functie meestal een gebogen vorm heeft, mag je
de twee punten x1 en x2 niet te ver uit
elkaar nemen, anders wordt het resultaat te onnauwkeurig. In figuur 308
geeft de pijl ongeveer de richting aan van de kromme lijn tussen de twee punten x1
en x2 . Je ziet echter dat de richting van de pijl niet klopt
bij x1 en evenmin klopt bij x2 . Pas als de
twee punten zeer dicht bij elkaar liggen, valt de richting van de pijl samen met
de richting van de kromme.
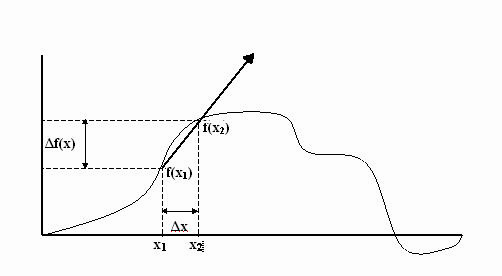
Fig. 308 Het differentiequotiënt
Je kan die punten net zo dicht bij elkaar nemen als je zelf
wil. Je moet ze alleen niet boven op elkaar nemen, want dan heb je geen
verschillen meer; dan valt er niets meer uit te rekenen. Over de vraag hoe dicht
de punten uiteindelijk bij elkaar moeten worden genomen, maakt niemand zich
druk, want ruim van tevoren zien we al aankomen waar het met het quotiënt Δf(x)/Δx
op uit zal lopen. We nemen de limiet voor Δx
gaat naar 0 (zo heet het als je Δx
steeds kleiner maakt) met het volgende symbool: 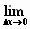
Wanneer je de limiet neemt van het genoemde quotiënt ben je
aan het differentiëren:
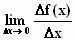
De verkorte schrijfwijze hiervoor is: 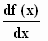 en de betekenis hiervan is de opdracht: "Bepaal de afgeleide functie van f(x)".
en de betekenis hiervan is de opdracht: "Bepaal de afgeleide functie van f(x)".
 |
Denk niet dat de letter d hier een functie is die
met f moet worden vermenigvuldigd. Het geheel is een symbolische
schrijfwijze voor het nemen van de limiet van het genoemde quotiënt. |
De bedoeling van het differentiëren is altijd het bepalen
van de mate waarin de functiewaarde f(x) verandert als de variabele x
van waarde verandert. Op de flanken van de "bergen" in de figuur
verandert de functiewaarde snel (= een grote waarde voor de
richtingscoëfficiënt), maar in de buurt van de top en het dal bijna niet (=
een kleine richtingscoëfficiënt) .
Voorbeeld:
Bepaal van de functie f(x) = 4 – x2 de
richtingscoëfficiënt in het punt x = 1.
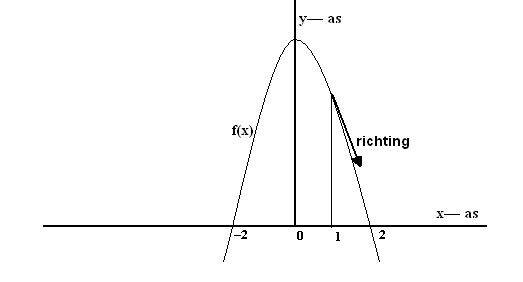
Fig. 309 De richtingscoëfficiënt
In dat punt heeft de functie een waarde f(1) = 4 – 12
= 3. We nemen, in gedachten, langs de x–as een tweede punt een
klein stukje, symbolisch aangegeven met Δx
, verderop. Dat wordt het punt 1 + Δx
. De functiewaarde die daarbij hoort is:
f(1+ Δx) = 4 – (1+
Δx)2 = 4 – {1 + 2. Δx
+(Δx)2 } = 3 – 2. Δx
– (Δx)2 .
Nu stellen we de limiet op:
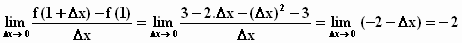
Je ziet, je rekent de functiewaarden in de twee dicht bijeen
gelegen punten gewoon uit, de getallen drie vallen tegen elkaar weg, je streept Δx
zoveel mogelijk weg en die ene Δx
die je overhoudt, daarvoor neem je de limiet naar nul, dat wil zeggen dat Δx
nul wordt, zodat je –2 overhoudt. Dat is het antwoord. Negatief, de
pijl wijst naar beneden.
Oefening 9
Bepaal zelf de afgeleide van de functie in het punt x = –2
.
 |
Rustplek.
(terug)
Hier treffen we de groep die het
allemaal nog wel zo’n beetje wist. |
|
We gaan weer terug naar de "vervaarlijke
vergelijking" voor τ die
we onderhanden hadden. Hij bestaat uit drie termen en er doen maar liefst vier
variabelen x′, y, z en t aan mee, waarbij y en z
gelukkig constant de waarde 0 blijven houden. Uit de vergelijking willen
we achterhalen hoe τ van x′
en van t afhangt. In onze beeldspraak van de cowboys op de balk: hoe kan τ
even groot voor cowboy A zijn als voor cowboy B als de laatste op
verschillende plaatsen op de balk gaat staan, waarbij voor ons zowel t
(door het "te vlug geschoten" effect) als x′
verschillende waarden aannemen.
We gaan de drie termen naar x′ differentiëren,
waarbij we het pad volgen dat Einstein heeft uitgezet.
De eerste term, het tijdstip van vertrek van het
signaal τ ( 0, 0, 0, t ) is in
deze vorm alleen maar afhankelijk van t. De x′, de y
en de z hebben hier de vaste waarde 0. Het tijdstip t waarop
het lichtsignaal werd uitgezonden, is volstrekt niet afhankelijk van de afstand x′
waar cowboy B zich bevindt ( t en x′ zijn helemaal
onafhankelijk van elkaar) en dat maakt het differentiëren naar x′
heel gemakkelijk, τ verandert
namelijk niet als x′ verandert:
De tweede term, het tijdstip in het stelsel–in–beweging
van terugkomst van het signaal in de oorsprong bij cowboy A, τ
( 0, 0, 0, { t + x′/(c–v) + x′/(c+v)})
is wél afhankelijk van x′, maar de afhankelijkheid zit niet in
de eerste coördinaat, want die is 0, maar in de tijdcoördinaat, de
laatste! Als x′ groter wordt, doet het signaal er langer over.
Hoe kunnen we nu differentiëren? Dat vraagt enige uitleg.
Voor de duidelijkheid geef ik de tijdcoördinaat t + x′/(c–v) + x′/(c+v)
voor de duur van de uitleg met het symbool T aan.
Dus T = t + x′/(c–v)
+ x′/(c+v).
De vraag is: hoe verandert de tijd τ
, die het tijdstip van terugkomst van het lichtsignaal aangeeft in het stelsel–in–beweging,
als x′ verandert? Daarvoor moet je eerst weten hoe de tijd T
verandert als x′ verandert om vervolgens te bezien hoe de tijd τ
in het stelsel–in–beweging verandert als T verandert. We komen hier
dus op de merkwaardige vraag hoe de tijd in het stelsel–in–beweging afhangt
van de tijd in het stelsel–in–rust.
Wiskundig, met de formules die we voor ons hebben, is dat
niet zo’n groot probleem. Want hoe je een functie differentieert naar een
variabele, die zelf weer verstopt zit in een andere functie, een zogenaamde
samengestelde functie, daar is de kettingregel voor uitgevonden. Maar
laten we proberen het te begrijpen, wat leuker is dan het domweg toepassen van
formules. De mate waarin de tijd τ
verandert, wordt gevonden door het effect van x′ op de tijd T
te vermenigvuldigen met het effect van T op de tijd τ
. Waarom vermenigvuldigen? Misschien dat oefening 10 dat duidelijk maakt.
 |
Oefening 10
Ieder uur dat de zon in het voorjaar extra schijnt, gaan er
100 mensen meer naar het plaatselijke strand. Verder is bekend dat als de
temperatuur in het voorjaar gemiddeld 1 °C stijgt, de zon gemiddeld 50 uur
extra schijnt.
Wat wordt de stijging van het aantal bezoekers van het strand
als de gemiddelde temperatuur 1,5 °C stijgt: 100 + 1,5 x 50 = 175 óf 100 x 1,5
x 50 = 7500? |
Je kijkt dus eerst naar het effect op het aantal uren
zonneschijn en daarna naar het effect op het aantal bezoekers en je ziet, wat je
ook al met je klompen aan voelde, dat het laatste antwoord goed is.
Dus als we de tweede term naar x′ willen
differentiëren, kunnen we het product nemen van een differentiatie van τ
naar T en van T naar x′ . Dit wordt de "kettingregel"
genoemd.
We werken het uit:

Je gebruikt hier een "kromme d" : de
"∂" om duidelijk te maken dat bij het differentiëren naar
één variabele, de andere variabelen constant worden gehouden. Je bekijkt dan
alleen het effect van die éne variabele op de waarde van de functie. De
snelheden c en v zijn in dit verband geen variabelen, c is
constant en v hóuden we constant, dus daar hoeven we ons geen
zorgen over te maken.
Bij wat er nu komt, moet je je heel goed concentreren. Mobiele telefoon uit.
Niet kletsen met elkaar!
We kijken eerst naar de term  .
Ik beweer .
Ik beweer 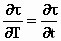 en ik leg het direct uit.
(Terug) en ik leg het direct uit.
(Terug)
De bewering klopt vanwege het volgende: beschouw T = t
+ x′/(c–v) + x′/(c+v) . We houden x′ constant –
dat is de bedoeling van de kromme d’s – en c en v zijn
constant, dan kan een verandering van T alleen maar het gevolg zijn van
een verandering van t , want de rest is constant.
 |
Onder een verandering van T wordt verstaan hoeveel T
groter of kleiner wordt, dus niet hoeveel kéér T groter of
kleiner wordt. Als bij t iets wordt opgeteld, komt er bij T evenveel bij.
Als t anderhalf keer zo groot wordt, wordt T niet ook anderhalf keer zo
groot. |
Dus 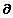 T = T = 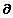 t
. Een verandering van t heeft eenzelfde verandering van T tot
gevolg als de rest constant is. t
. Een verandering van t heeft eenzelfde verandering van T tot
gevolg als de rest constant is.
Vervolgens kijken we naar de term 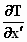 .
Deze werken we uit. .
Deze werken we uit.
De tijd T = t + x′/(c–v) + x′/(c+v)
bestaat uit drie termen.
We passen de regel uit de wiskunde toe dat de afgeleide van
een som gelijk is aan de som van de afgeleiden en differentiëren de
afzonderlijke termen. Het resultaat wordt:

De eerste term wordt nul omdat t niet afhankelijk is
van x′, zoals we eerder hebben gezegd. Die nul laten we verder
natuurlijk weg.
De uitkomst van de tweede en de derde term vind je door te
differentiëren. Als je weet dat de afgeleide van x′ naar x′
gelijk is aan 1 (een verandering van x′ gaat gelijk op met
een verandering van x′ , logisch) dan zie je het antwoord meteen,
want x′/(c – v) verandert natuurlijk veel minder dan x′
omdat de verandering ook door (c – v) wordt gedeeld.
De formule, die eerder "kettingregel" is
genoemd, kunnen we nu met de gevonden resultaten uitwerken:
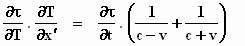
We schrijven dit in een andere volgorde om het in
overeenstemming te brengen met het linker deel van de vergelijking bovenaan p.
899 van het origineel. Dus:

Nu vergeten we de ingevoerde T weer omdat de uitleg is
afgelopen.
Dit was al lastig, maar nu komt het moeilijkste obstakel van
het eerste deel van deze tocht. De derde term, na het = teken, van de "vervaarlijke
vergelijking". Houd de concentratie vast! De derde term is het tijdstip
τ waarop de lichtstraal bij
cowboy B wordt weerkaatst. Daarin zit de variabele x′ zowel
in de eerste plaatscoördinaat als in de (laatste) tijdcoördinaat:
τ ( x′,
0, 0, t + x′/(c–v)) .
Wat is hier de invloed van x′ op de tijd τ
? We halen de letter T weer tevoorschijn maar nu met een
nieuwe inhoud: T wordt t + x′/(c–v) . We krijgen τ
(x′, 0, 0, T).
Je hebt nu te maken met een directe invloed van x′
op τ via de eerste coördinaat
en een indirecte invloed via de laatste coördinaat. Hoe verandert τ
als x′ verandert. Dat wordt weer aangepakt met de kromme d’s
waarbij we differentiëren naar de ene variabele terwijl we de andere variabelen
constant houden. Je kan ook zeggen dat je de verandering van τ
bekijkt precies in één richting of langs één coördinaat.
De afgeleide in de eerste richting langs de x–as,
waarbij de andere coördinaten constant worden gehouden, dus ook T = constant,
schrijven we als:

Hiermee wordt de invloed: "te vlug geschoten"
beschreven.
De y– en z–coördinaat zijn constant 0
, dus de afgeleide in die richting naar x′ is ook altijd 0.
Als we de afgeleide naar de tijdcoördinaat T bekijken, houden we die
natuurlijk niet constant. We nemen dan juist de eerste richting constant. We
kijken op een bepaalde plaats x′ en we zoeken de invloed op τ
als de tijd die de lichtstraal er over doet volgens ons om van A naar B
te gaan verandert door een kleine verplaatsing van het punt x′ .
Hier passen we de kettingregel opnieuw toe:
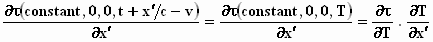
Met eenzelfde redenering over de gelijke invloed
van T
op τ en t op τ
als bij de tweede term (zie aldaar) mogen we weer stellen: 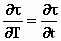 . .
De term ¶T/¶x′
werken we uit, met in gedachten de opmerking dat x′ en t
geheel onafhankelijk van elkaar zijn:
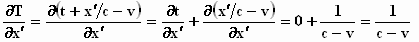
De verandering van τ wordt
de som van de directe verandering door x′ als plaatscoördinaat,
namelijk 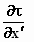 , en de
indirecte verandering, namelijk , en de
indirecte verandering, namelijk 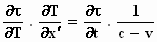 door zijn effect op de tijdcoördinaat.
door zijn effect op de tijdcoördinaat.
|
Waarom nu de som? Omdat je eerst de verandering van τ
bekijkt als x′, de eerste coördinaat, verandert terwijl je de
andere coördinaten constant houdt en vervolgens de verandering van τ
bekijkt als de laatste coördinaat verandert als gevolg van een
verandering van x′, terwijl je dan de eerste drie coördinaten
constant houdt. De twee veranderingen hebben geen invloed op elkaar, ze werken
allebei direct op τ. Het zijn
twee onafhankelijke effecten op τ
en daarom moet je ze optellen. Oefening 11 maakt die onafhankelijkheid
verder duidelijk.
 |
Oefening 11
Als de temperatuur in Europa gemiddeld 1 °C stijgt, komt er
via de Rijn 50 m3/s meer smeltwater uit de bergen van Zwitserland en
als het in Europa gemiddeld 1 °C warmer wordt, valt er tegelijkertijd in het
stroomgebied van de Rijn meer regen, zodat de Rijn als gevolg daarvan 400 m3/s
meer regenwater afvoert. Hoeveel meer water voert de Rijn af als het in Europa
gemiddeld 1 °C warmer wordt? 400 + 50 = 450 of 400 x 50 = 20 000 m3/s?
|
Het eerste antwoord is goed. Het is niet zo dat het méér
gaat regenen als er meer smeltwater uit de bergen komt, noch dat er meer
smeltwater uit de bergen komt als het in het stroomgebied meer gaat regenen. De
twee verschijnselen versterken elkaar niet, maar dragen wél beide mee,
onafhankelijk van elkaar, aan een grotere waterstroom in de Rijn.
Het resultaat van de differentiatie van de derde term levert
een bruikbare nieuwe schrijfwijze:
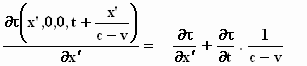
(We mogen de tijdelijke inhoud van T weer
vergeten).
We zetten de resultaten links en rechts van het =teken van de
"vervaarlijke vergelijking" bij elkaar:
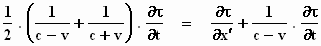
Dit is precies de formule die Einstein kort door de bocht had
opgeschreven bovenaan p. 899.
Terug
De vergelijking wordt vervolgens herschikt om er een
hanteerbare differentiaalvergelijking van te maken.We brengen alle termen links
van het =teken en we tellen de twee ∂τ/∂t
termen bij elkaar op. Let op de veranderingen van + en –tekens!
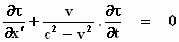 "differentiaalvergelijking"
"differentiaalvergelijking"
Dit is een zeer belangrijke formule. Alvorens we ermee verder
gaan, maakt Einstein twee opmerkingen.
 |
De eerste is dat de lichtstraal niet perse uit de oorsprong
had behoeven te worden verzonden om dit resultaat te bereiken. Dat de
vergelijking dus voor iedere waarde van x, y, z geldig is. Hoe duiden we
deze opmerking?
Indien we voor de x-coördinaat in plaats van 0
een andere vaste waarde x0 kiezen en evenzo voor de y–coördinaat
en de z–coördinaat de vaste waarden y0 en z0
kiezen, kunnen we dezelfde wijze van differentiëren op de vergelijking
toepassen. Juist omdat x0 en y0 en z0
vaste waarden zijn, leveren ze geen bijdragen bij het differentiëren naar x′. |
 |
De tweede is dat we tot nu toe de coördinaten
y en z
constant hielden. Daarom speelden ze geen rol. We onderzoeken toch even hoe de
tijd τ van de coördinaten y
en z afhangt door ook in die richtingen een lichtstraal af te vuren.
"Die afhankelijkheid is nul komma nul", zegt
Einstein. |
Dat willen we wel eens zien en we controleren het voor de
verticale richting (zie figuur 310).
We sturen een lichtsignaal langs de ζ–as
van het stelsel–in–beweging naar een spiegeltje in
het punt z en weer terug. Vanuit het stelsel–in–rust
gezien, vormt de weg van het lichtsignaal een gelijkbenige driehoek. omdat het
stelsel–in–beweging zich verplaatst tijdens de reis van het lichtsignaal.
Bij de schuin staande benen van de driehoek hoort de snelheid c . De
snelheid in de ζ–richting van het
lichtsignaal is 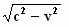 . .
Via dezelfde aanpak die tot de "vervaarlijke
formule" leidde, verkrijgen we dan de vergelijking:
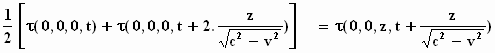
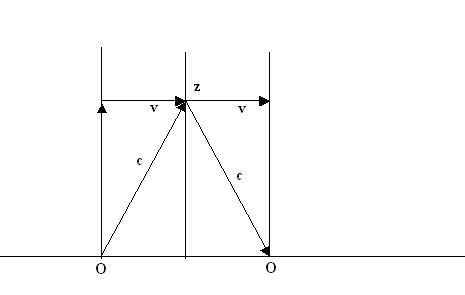
Fig. 3.10 Het lichtsignaal gaat van O naar z en weer naar O.
Het stelsel beweegt met snelheid v .
Differentiëren naar z levert:
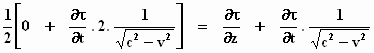
Als je tegen elkaar wegstreept wat links en rechts gelijk is
aan elkaar, houden we over:
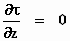
Er is géén afhankelijkheid. Op identieke wijze vinden we: 
Einstein heeft gelijk, alweer! De tijd τ
hangt niet af van y of z.
We gaan terug naar de "differentiaalvergelijking"
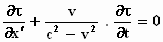
Einstein poneert vervolgens boudweg dat, vanwege de aanname dat de
functie τ lineair was, de
functie de volgende vorm moet hebben:
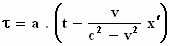 "een
oplossing"
"een
oplossing"
Hoe komt hij daarbij?
Hierin is a een constante factor, niet afhankelijk van
v of van x´ . Als je namelijk een
functie voor τ hebt gevonden die
aan de "differentiaalvergelijking" voldoet, "een oplossing",
dan voldoet een functie die a keer zo groot is ook
omdat beide afgeleiden in de differentiaalvergelijking dan a keer zo groot worden. Verder is het een kwestie
van stomweg controleren of de oplossing voldoet door τ
te differentiëren naar x′ en naar t en te onderzoeken of
het klopt:

Verdraaid, als je dat invult in de "differentiaalvergelijking"
dan klopt het! Doe het even! Je ziet tevens dat a voor spek en bonen meedoet. Dus het
klopt. Het is een oplossing van de vergelijking.
Je ziet bovendien dat in de oorsprong (x′ = 0)
op het tijdstip t = 0 ook geldt τ =
0. Dat is een keuze om de optredende integratieconstante gelijk aan
nul te krijgen, erg handig en dat mag omdat je ieder tijdstip altijd als
nulpunt voor de tijd kan kiezen, behalve in de kosmologie.
 |
Het absolute nulpunt van de tijd, de
oerknal, is voor het dagelijks gebruik te onnauwkeurig en het rekent
lastig. |
Je bent geneigd te denken dat de factor a wel gelijk
zal zijn aan één, zodat hij lekker makkelijk wegvalt, maar Einstein toont aan
dat hij juist niet gelijk is aan één. Heel essentieel!
Laten we eerst eens kijken waar Einstein naartoe wil. Zoals
je weet was x′ een vast punt in het stelsel–in–beweging waarvan
de plaats verder niet was vastgesteld. Er gold: x′ = x – v.t Als
we dit in de formule van τ voor x′
invullen, verkrijgen we een uitdrukking voor τ
(de tijd in het stelsel–in–beweging) die alleen nog maar afhangt van de
coördinaten x en t uit het stelsel–in–rust. Daar moeten we
naartoe, want dan hebben we een brug geslagen tussen de twee stelsels:
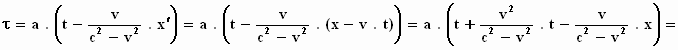
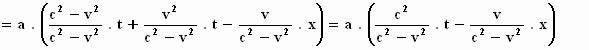
dus 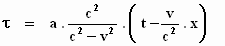
We zien hoe de tijd τ
afhangt van de tijd t en de plaats x in het stelsel–in–rust.
De coördinaat voor de tijd τ in
het stelsel–in–beweging is nu geheel uitgedrukt in de coördinaten voor tijd
t en plaats x van het stelsel–in–rust. Dat is de bedoeling.
De volgende stap is erachter te komen hoe de ξ–coördinaat
in het stelsel–in–beweging afhangt van de coördinaten x, y, z, t in
het stelsel–in–rust. Laten we Einstein volgen. Hij laat hier een prachtige
gedachtegang zien voor de bepaling van de ξ–coördinaat.
In het stelsel–in–beweging heeft de lichtstraal namelijk ook de snelheid c
. Op het moment dat de lichtstraal uit de oorsprong van het stelsel–in–beweging
vertrek, vallen de oorsprongen samen en er geldt in dat punt t = τ
= 0 De plaats die de lichtstraal bereikt na een tijd τ
(de tijd in het stelsel–in–beweging) is:
ξ = c . τ
Het tijdstip in het punt ξ
is dan τ. Nemen we voor ξ
het punt x′ dan mogen we voor τ
schrijven 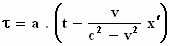 , waarbij t de tijd is
die de lichtstraal er volgens ons over doet om het punt x′ te
bereiken. Zo krijgen we: , waarbij t de tijd is
die de lichtstraal er volgens ons over doet om het punt x′ te
bereiken. Zo krijgen we:
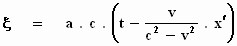
Terug
|
|
|
|
|
We mogen t vervangen door de tijd die de lichtstraal er volgens ons
over doet, namelijk: 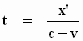 . Dat vullen we in en we werken het direct uit:
. Dat vullen we in en we werken het direct uit:
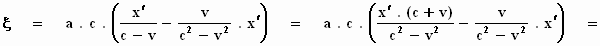
(Bedenk dat (c – v) . (c + v) = c2 – v2
)
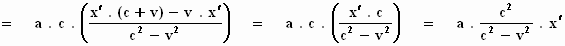
Ook hier kunnen we x′ = x – v . t invullen,
zodat ξ net als τ
uitsluitend in coördinaten van het stelsel–in–rust is uitgedrukt, en dan
rolt de volgende formule uit de bus:
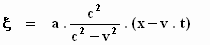
Dat gaat goed! We hebben al twee van de vier coördinaten te
pakken, namelijk τ en ξ
en die andere twee, namelijk η
en ζ , dat moet een makkie zijn.
We komen er aan!
Als we in de η–richting
een lichtstraal tot een bepaald punt η verzenden,
dan geldt voor die afstand η = c . τ.
Voor τ vullen
we de formule in die x′ bevat en omdat x′= 0 (het is
immers een beweging langs de η – as)
volgt er uit:

Het punt η komt
natuurlijk overeen met een of ander punt y in het stelsel–in–rust.
Vanuit het stelsel–in–rust gezien is de tijd die het licht erover doet om
dat punt y te bereiken (vergelijk figuur 310):
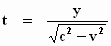
Dus, als we t invullen in de uitdrukken voor η
, krijgen we:
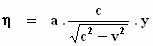
Op dezelfde manier wordt de uitdrukking voor de ζ–richting
verkregen:
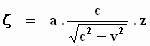
We hebben ze! Alle vier! Er moet alleen nog wat aan worden
geschaafd, maar we zijn door het moeilijkste heen. Gefeliciteerd. Wat een zware
afleidingen! Het leek wel een bergetappe! We hebben Einstein goed kunnen volgen
en we laten hem niet meer ontsnappen. We raken er steeds bedrevener in. Einstein
moet niet denken dat wij hem niet zouden begrijpen. Dan kent ie ons nog niet!
Hij is nog niet van ons af!
Op ons gemak zetten we de formules die we tot nu toe hebben
gevonden bij elkaar. Om de overzichtelijkheid te bevorderen, schrijven we 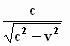 in
de vorm in
de vorm 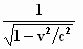 . .
De formules om de coördinaten van het stelsel–in–rust om
te zetten in die van het stelsel–in–beweging zijn de transformatieformules.
Hier zijn ze:
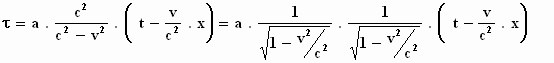
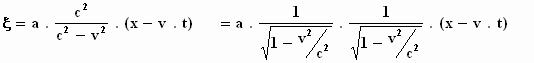


Je denkt dat je er al bent, maar de constante a moet
nog worden bepaald. Einstein gaat ons al voor. Hij maakt een geniale
gedachtesprong om de waarde van a te achterhalen. Hoogste tijd om de
achtervolging in te zetten.
Uit de manier waarop de factor a bij de formule voor τ
opdook, blijkt dat hij constant is voor tijd en plaats, maar hij zou
een functie kunnen zijn van v , want bij de eerdere bewerkingen werd er
niet naar v gedifferentieerd, zodat een dergelijke afhankelijkheid niet
tot uiting kon komen. Einstein stelt ten bate van de overzichtelijkheid het
volgende voor:
"Als je die term 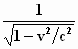 vervangt door
het symbool γ (gamma) en je
vervangt vervangt door
het symbool γ (gamma) en je
vervangt 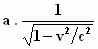 door de functie φ(v)
, dus φ(v) = a . γ , dan
worden de formules een stuk eenvoudiger". door de functie φ(v)
, dus φ(v) = a . γ , dan
worden de formules een stuk eenvoudiger".
Dus met 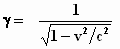 en φ(v)
= a . γ
en φ(v)
= a . γ
verkrijg je:
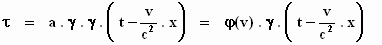



De vraag over de betekenis van de factor a is nu
verlegd naar de betekenis van φ(v)
!
 |
Wie de originele Duitse tekst erbij pakt, zal zien dat
Einstein niet de γ, maar de
Griekse letter β als symbool
voorstelde. De letter β was
echter al in gebruik, onder andere door Lorentz, voor het quotiënt v/c
dus β = v/c . In de meeste
hedendaagse literatuur wordt voor 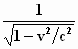 de
γ gebruikt als symbool.
Einstein heeft dit pleit verloren. de
γ gebruikt als symbool.
Einstein heeft dit pleit verloren. |
Voor we met φ(v) verder
gaan,
wil Einstein eerst even iets bewijzen, namelijk dat als je ervan uitgaat dat in
het stelsel–in–rust iedere lichtstraal de snelheid c heeft, dat dan
diezelfde lichtstralen in het stelsel–in–beweging ook de snelheid c
hebben. Hij wil dit bewijzen, zegt hij, omdat het bewijs nog niet is geleverd
dat het principe van de constantheid van de lichtsnelheid te verenigen is met
het relativiteitsbeginsel.
Het merkwaardige is dat we daar eigenlijk helemaal niet aan twijfelden.
Bovendien hebben we eerder in dit verhaal al gebruik gemaakt van een vaste
lichtsnelheid c in het stelsel–in–beweging om de ξ–,
η– en ζ–coördinaten
te bepalen. Sterker, de afleiding van de τ–coördinaat
berust geheel op het principe van een vaste lichtsnelheid c in ieder bewegend
stelsel.
"Vervallen we niet in een cirkelredenatie?"
Jazeker, hier gleed Einstein uit! Hij had teveel haast. Hij schreef in dat
jaar vijf baanbrekende artikelen en dan moet je niet verbaasd opkijken als
ergens een slordigheidje opduikt. Dat zou jou ook kunnen overkomen, geef toe.
Bovendien wist Einstein dat verschillende geleerden van naam ook weer met
publicaties zouden komen over het onderwerp "Elektrodynamica", (hij
kon niet vermoeden dat ze voorlopig nog niet op zijn spoor zaten), dus schreef hij
in haastige spoed.
De vraag is wat Einstein wilde bewijzen en wat hij uiteindelijk bewees. Hij
wilde bewijzen dat de beide grondbeginselen met elkaar te verenigen zijn. Dit
slaat terug op zijn opmerking aan het eind van p. 891 over de schijnbare
tegenspraak tussen het relativiteitsprincipe en de constante lichtsnelheid in
ieder bewegend stelsel. Het is een schijnbare tegenspraak en omdat hij bij de
afleiding van de transformatieformules volop gebruik heeft gemaakt van diezelfde
constantheid van de lichtsnelheid, kan het volgende niet als een bewijs, maar
uitsluitend als een illustratie worden gezien.
Laten we de twee beginselen, de aannames, nog eens aangescherpt onder de loep
nemen:
1ste: Overal in het heelal waar onze bekende mechanicawetten
gelden, zullen ook onze wetten van de elektrodynamica en de optica, kortom alle
natuurwetten, geldig zijn.
2de: In de lege ruimte beweegt het licht zich altijd voor iedere
waarnemer voort met een vaste snelheid die niet afhangt van de snelheid van het
voorwerp dat het licht heeft uitgezonden.
We volgen Einstein: hij neemt een lichtgolf in het stelsel–in–rust die zich in alle
richtingen uitbreidt en op het tijdstip t een bol heeft gevormd met de
straal c . t . Hij laat zien dat dezelfde lichtgolf in het stelsel–in–beweging
gemeten ook een bol vormt, maar dan met de straal c . τ
. Dus in het stelsel–in–beweging, met de daar geldende tijd, heeft het licht
ook de snelheid c . Dat vormt een mooie illustratie voor de theorie
van de coördinatentransformaties.
Dat gaan we na. Maar wat is ook alweer een bol? Je zou van minder de kluts
kwijtraken!
Voor een boloppervlak met een straal R , waarvan het centrum in de
oorsprong van het assenstelsel met een x–as, een y–as en een z–as,
ligt, geldt de volgende vergelijking:
x2 + y2 + z2 = R2 Formule
voor een bol oppervlak
Daar kijken we even rustig naar. Wat heeft dat met een bol te maken?
Probeer het volgende eens: neem x = 0 en y = 0 . Dat kan, dat
is bij de oorsprong, alleen z kan dan niet gelijk aan 0 zijn,
anders zou x2 + y2 + z2 ook gelijk zijn
aan nul. Dat moest juist gelijk aan R2 worden. Daarom moet
voor z gelden z = R of wat ook kan: z = – R. Op dezelfde
manier kijk je naar: x = 0 en z = 0, dan krijg je y = R (of
– R) en tenslotte met y = 0 en z = 0, dan krijg je x = R
(of – R). Die punten x = R , y = R en z = R liggen
allemaal even ver weg van de oorsprong, evenals x = – R ; y = – R
en z = – R. Met de formule worden niet alleen deze zes punten, maar
alle punten aangegeven die op een afstand R van de oorsprong liggen. Dat
is een bol!
Nu volgen we Einstein weer even op de voet: De bolvormige lichtgolf laten we
ontstaan in de oorsprong van beide stelsels op het moment dat de oorsprong van
het stelsel–in–beweging samenvalt met de oorsprong van het stelsel–in–rust.
Voor dat moment laten we gelden t = 0 en τ
= 0. Na enige tijd heeft in het stelsel–in–rust de lichtgolf zich
bolvormig uitgebreid tot een straal R = c . t . Dan geldt:
x2 + y2 + z2 = (c .t)2
Met behulp van de transformatieformules willen we dit omrekenen, maar daartoe
moeten we eerst de gevonden transformatieformules van het stelsel–in–rust
naar het stelsel–in–beweging omwerken tot transformatieformules van het
stelsel–in–beweging naar het stelsel–in–rust. De andere kant op. Je
voelt wel aan dat het sneller moet kunnen, dat de transformatie de ene kant op
eigenlijk hetzelfde is als de andere kant op, maar dat is achteraf gepraat.
Einstein wil laten zien dat als de lichtsnelheid in het ene stelsel gelijk is
aan c , en dat stelsel hebben we het stelsel–in–rust genoemd, de
lichtsnelheid in het andere stelsel, het stelsel–in–beweging, ook c
is. We mogen dus niet het stelsel–in–beweging als uitgangspunt nemen.
"Na een simpele berekening", zegt Einstein. Dat geeft de burger moed
De tocht is weliswaar eenvoudig, maar je maakt heel gemakkelijk kleine fouten
waardoor je in de moeilijkheden komt en veel tijd verspeelt. Als je niet erg
vaardig bent in de algebra en je hebt de tijd, dan is de komende omrekening een
prachtige oefening in het toepassen van allerlei rekenregels uit de algebra.
Gewoon doen! Veel succes, we zien elkaar straks weer.
Start met het herschrijven van de transformatieformules in de andere
richting. Die zijn voor y en z gemakkelijk te vinden, gewoon door
ze om te keren:
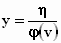 en
en 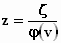
De x en de t zitten echter verstopt in de vergelijkingen voor ξ
en voor τ. We moeten deze twee
vergelijkingen tegelijkertijd aanpakken als twee vergelijkingen met twee
onbekenden. We herschrijven ze zo dat we door optellen de tijd t er uit
kunnen gooien (elimineren).
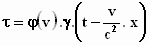
Delen door φ(v).γ
geeft 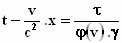 (1)
(1)
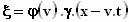
Delen door φ(v).γ.v
geeft  (2)
(2)
We tellen de termen links van het =teken van de formules (1) en (2)
bij elkaar op. Dat moet gelijk zijn aan de som van de termen rechts van het
=teken. Zo krijg je na enig gepuzzel:
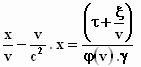
Vermenigvuldig alle termen van de laatste regel met v en zet x
buiten haakjes. Je krijgt:

Let op de term (1– v2/c2), want die is precies
gelijk aan 1 / γ2 .
Ter herinnering: 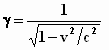
Dus:
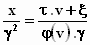
Aan beide kanten met γ2
vermenigvuldigen en de boel iets overzichtelijker opschrijven,levert:
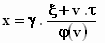
*dit is de transformatieformule voor x: als je ξ
en τ weet, kan je hiermee x
berekenen en als je x weet kan je x in ξ
en τ uitdrukken.
Om vervolgens de transformatieformule voor t te vinden, vervangen we x
in de vergelijking die met (1) is aangegeven door de net gevonden formule
voor x met het gevolg dat we t in τ
en ξ kunnen uitdrukken. We werken dit
in kleine stapjes uit.
Dus : 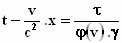 wordt met
wordt met 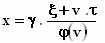 : :
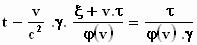
|
|
We brengen t links van het = teken en alle andere termen naar rechts:
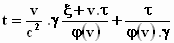
Eigenlijk zijn we klaar, maar voor de overzichtelijkheid fatsoeneren we alles
wat achter het =teken staat door eerst 1 / φ(v)
buiten haakjes te brengen:
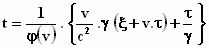
Wat tussen de accolades staat werken we verder uit. Eerst de kleine haken
wegwerken:
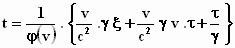
en dan weer 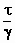 buiten haakjes zetten:
buiten haakjes zetten:
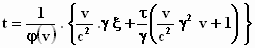
De term 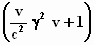 =
=  nemen we even apart:
nemen we even apart:
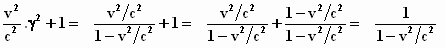
De laatste term is precies γ2
. Dat vullen we in voor 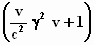 : :
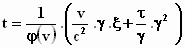
Haal γ voor de haakjes en
verander de volgorde :
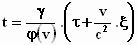
*Dat is hem dan, dit is de
transformatieformule voor t: als je ξ
en τ weet, kan je hiermee t
berekenen en als je t weet kan je t in ξ
en τ uitdrukken.
Eindelijk, het kostte wat moeite, maar nu hebben we alle vier de
transformatieformules van het stelsel–in–beweging naar het stelsel–in–rust.
Dus met (ξ, η, ζ, τ)
bereken je (x. y, z, t) .
Je ziet dat de formules inderdaad bijna hetzelfde als de uitgangsformules
zijn. Als t vervangen wordt door τ,
enzovoort, en als ook v wordt vervangen door –v komt het op
hetzelfde neer. De enige afwijking is dat er in plaats van φ(–v)
staat 1/φ(v).
Kennelijk is φ(–v) = 1/φ(v).
Onthoud dat, dat gebruiken we nog bij de bepaling van φ(v).
Nu vullen we de vergelijking x2 + y2 + z2
= (c .t)2 in want het ging er om het bewijs te leveren dat het
licht zich in het stelsel–in–beweging ook met de lichtsnelheid c
voortbeweegt:

We verwijderen ogenblikkelijk φ(v)
, die in alle termen voorkomt, want die heeft ons de hele tijd al in de weg
gezeten. Dan krijgen we:
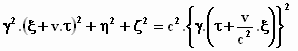 , en werken
dit verder uit:
, en werken
dit verder uit:
[ Ter herinnering : (a + b)2 = a2 + 2.a.b + b2
]
γ 2 . (ξ2
+ 2.ξ . v . τ
+ v2 . τ2 ) + η2
+ ζ2 = c2 .γ2
.{τ2 + 2 .τ
.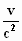 . ξ
+ . ξ
+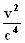 .ξ2} .ξ2}
De dubbele producten (met die 2 ervoor) links en rechts vallen tegen
elkaar weg (de rechterkant eerst vermenigvuldigen met c2):
γ 2 . (ξ2
+ v2 . τ2 ) + η2
+ ζ2 = c2 . γ2
.{τ2 +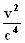 .ξ2} .ξ2}
We zetten dit in een andere volgorde: de termen met ξ2
naar links en die met τ2
naar rechts; even puzzelen:
γ 2 . (ξ2
–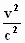 . ξ2)
+ η2 + ζ2
= c2 . γ2 (τ2
– . ξ2)
+ η2 + ζ2
= c2 . γ2 (τ2
– 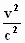 . τ2) . τ2)
en nu komt de factor γ2
weer tevoorschijn als 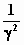 = (1– = (1–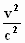 )
als je ξ2
respectievelijk τ2
buiten haakjes zet: )
als je ξ2
respectievelijk τ2
buiten haakjes zet:
γ 2 . ξ2
. (1–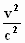 ) + η2
+ ζ2 = c2 .γ2
τ2 . (1– ) + η2
+ ζ2 = c2 .γ2
τ2 . (1–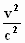 ) )
Daar valt heel wat weg te strepen en je houdt plotseling over:
ξ2 + η2
+ ζ2 = c2 . τ2
* Je hebt het bewijs geleverd! Goed gedaan!
 | Rustpunt: Doe even een geestelijke
ontspanningsoefening of bel je moeder! |
Hiermee hebben we bewezen dat als de lichtgolf in het stelsel–in–rust
zich bolvormig uitbreidt hij zich ook in het stelsel–in–beweging bolvormig
uitbreidt en dat de straal na τ
seconde de waarde c . τ heeft,
zodat de snelheid van het licht in het stelsel–in–beweging ook in alle
richtingen de waarde c heeft.
Hier had Einstein ons goed te pakken genomen. "Een simpele berekening,
ja, m’n grootje, die is simpel!". Het was een niet te onderschatten
afleiding met het nodige risico de weg kwijt te raken. Moeilijkheidsgraad
minstens 5, denken wij. Een rode route, mogelijk zelfs zwart! En bovendien
overbodig!
Terug
Nu gaan we toch eindelijk uitzoeken wat φ(v)
te betekenen heeft. Probeer je goed te concentreren! Als tip krijgen we mee er
een derde (!) coördinatenstelsel K* in te betrekken. Toe maar! Met de
coördinaten x*, y*, z* en t* . Op het tijdstip t = 0 laten
we de drie oorsprongen samenvallen. Aan het laatste stelsel wordt ten opzichte
van het tweede stelsel k een snelheid –v gegeven. Wat een
kermis! Je zou jer duizelig van worden, ware het niet dat het derde
stelsel de beweging van k juist opheft. Ten opzichte van het eerste
stelsel K staat K* stil! De stelsels K en K* zijn
eigenlijk hetzelfde (zie figuur 311).
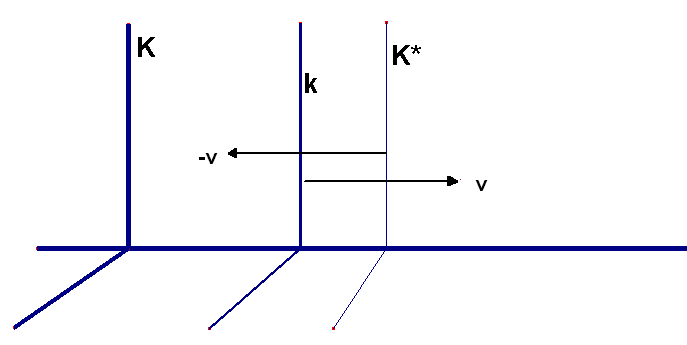
Fig. 3.11 Drie stelsels: K, k en K*
De gang van zaken is nu de volgende: De coördinaten van K* worden
uitgedrukt in de coördinaten van k en vervolgens worden de coördinaten
van k uitgedrukt in de coördinaten van K. Bij de eerste transformatie wordt k als stelsel–in–rust opgevat en
bij de tweede wordt K als stelsel–in–rust opgevat. En daar moeten we welgemoed de transformatieformules op loslaten. We drukken t*
uit in τ en τ
vervolgens weer in t. Logischerwijs moeten t* en t gelijk
aan elkaar zijn, omdat stelsel K* identiek is aan stelsel K .
Hetzelfde geldt voor x* , y* en z*.
We zullen één zo’n aan elkaar geregen transformatie volgen. Die voor de
tijd. We schrijven de transformatie van k naar K* op en vullen dan
de transformatieformules voor τ
en ξ van K naar k
in. Het lijkt een dingetje van niks, maar het valt toch nog wel tegen.
Om t* te vinden wordt dezelfde transformatieformule gebruikt als voor τ
. Nu echter moeten we in de formule τ
vervangen door t* , t vervangen door τ
en x vervangen door ξ.
Verder moeten we in plaats van de snelheid v nu de snelheid –v
nemen. Doet iedereen even mee! Hier komt de uitwerking:
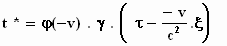
In deze uitdrukking vullen we de formules voor τ
en ξ worden in en we werken dat
uit:

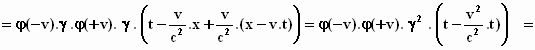
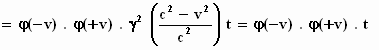
Herinner je je dat 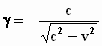 ,
,
dan zie je dat
bij de laatste stap γ2
precies wegvalt tegen  . .
Zoals eerder gezegd, moet t* gelijk zijn aan t.
Dus: t* = φ(–v) . φ(+v)
. t = t
Op dezelfde manier kan je laten zien dat :
x* = φ(–v).φ(+v).
x = x
y* = φ(–v).φ(+v).
y = y
z* = φ(–v).φ(+v).
z = z
 | Oefening 12
Laat eens zien dat de laatste formule klopt. |
Zie je wel, na een kleine inspanning een mooi resultaat. Hiermee moeten we
verder kunnen komen.
Omdat t* gelijk moet zijn aan t volgt daaruit dat φ(–v)
. φ(+v) = 1. Zoiets hebben we eerder gezien. De identieke
transformatie, zoals Einstein dat noemt, omdat vermenigvuldigen van de tijd t
met φ(–v).φ(+v) weer t
oplevert . Het zou lichtvaardig zijn om te denken dat φ(+v)
én φ(–v) dan wel gelijk
zullen zijn aan 1 .
We moeten ons afvragen wat de betekenis is van de functie φ(v)
. Einstein besteedt er in het artikel verhoudingsgewijs veel ruimte aan. We
blijven even in de buurt van Einstein, hij weet de weg en hij laat ons een mooi
stukje logica zien.
Kijk naar het stuk van de ζ-as
in het stelsel–in–beweging k dat zich uitstrekt vanaf de oorsprong
tot een punt 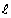 (zie
figuur 312).
(zie
figuur 312).
De lengte van dit stuk as is dus 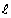 .
.
Uit de transformatieformule: ζ = φ(v)
. z
volgt, met ζ = 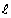
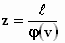
Uit de laatste formule zie je dat de functie φ(v)
aangeeft in welke mate de lengte van dit stuk as (en dus eigenlijk iedere lengte
loodrecht op de bewegingsrichting) kleiner of groter wordt waargenomen in het
stelsel–in–rust dan in het stelsel–in–beweging. Als de lengte echter
verandert, kan het uitrekken of krimpen van de lengte onmogelijk afhankelijk
zijn van de bewegingsrichting. Stel je eens het volgende voor:

Figuur 312 De lengte ℓ of ℓ/φ(v)
in de z–richting
Een balk passeert ons met grote snelheid van links naar rechts en we zien dat
de rechtopstaande cowboys zijn gekrompen. We herhalen de proef, maar we gaan aan
de andere kant staan, zodat voor ons de balk van rechts naar links beweegt. Het
zou toch wel heel gek zijn als de cowboys ineens waren gegroeid. Het kan niet
omdat er anders in de lege ruimte, in het heelal een voorkeursrichting zou
bestaan. Dan zou je boven en onder in het heelal kunnen onderscheiden. Niets
wijst daarop, dus als ze van links naar rechts bewegend gekrompen zijn, dan zijn
ze ook van rechts naar links bewegend gekrompen. Een lengteverandering moet voor
beide richtingen + v of – v in dezelfde mate gelden. Maar dat
betekent:
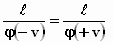
of:
φ(–v) = φ(+v)
Als je dit combineert met: φ(–v) .
φ(+v) = 1
kan je er van maken: φ(+v) . φ(+v)
= 1
dus
φ(+v) = 1
en ook
φ(–v) = 1 .
De oplossing φ(+v) = –1 en φ(–v)
= –1 voldoet niet omdat dan alles wat zich in beweging zet op zijn
kop zou moeten staan. Dat verschijnsel doet zich simpelweg niet voor!
Ha, ha, ha, er komt toch het getal één uit. De cowboys waren dus gekrompen
noch gegroeid! De afmetingen loodrecht op de bewegingsrichting blijven
onveranderd!
Te gek, zo’n logische redenering!
|
Nu schrijven we de transformatieformules in hun definitieve en tevens
eenvoudigste vorm, van alle rommel ontdaan.:
Transformatieformules .
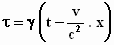

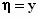
ζ = z
met 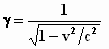
Deze transformatieformules werden al eerder dan door
Einstein afgeleid door W. Voigt (in 1877) voor een ander natuurkundig probleem
en door H.A.Lorentz in zijn "Versuch einer Theorie" uit 1895.
Poincaré had dit stel formules al de Lorentztransformatieformules genoemd.
 |
Jules Henri Poincaré, Frans wiskundige en
wetenschapsfilosoof. Geboren in Nancy in 1854 en gestorven in Parijs in
1912. Men fluistert dat als Einstein de relativiteitstheorie niet had
ontdekt, dat Poincaré een goede kans op die ontdekking zou hebben gehad. |
Nog even iets over γ . Dit
symbool staat voor:
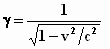
Je moet je realiseren dat altijd zal gelden: γ
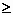 1,
want 1,
want 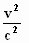 kan waarden
krijgen van nul tot en met één en daarom zal de term (1 – kan waarden
krijgen van nul tot en met één en daarom zal de term (1 – 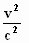 )
ook altijd waarden hebben van nul tot en met één. Ook de term )
ook altijd waarden hebben van nul tot en met één. Ook de term 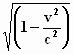 kan
slechts waarden krijgen die van nul tot en met één lopen kan
slechts waarden krijgen die van nul tot en met één lopen
 | Voor een bewegend voorwerp in het dagelijks leven, zoals een auto of een
tennisbal, wijkt de term niet noemenswaardig af van één. Alleen zeer
kleine elektrisch geladen deeltjes in de buis van een TV–toestel of in een
TL–buis behalen snelheden die er toe doen. Voor licht, en aanverwante
straling, dat zich met de lichtsnelheid voortbeweegt, is de term precies
nul. |
Maar het omgekeerde van een getal tussen 0 en 1 is een getal
dat groter is dan 1. Als het getal weinig kleiner is dan 1 is het
omgekeerde weinig groter dan 1. Maar als het getal in de buurt van 0
komt, dat wil zeggen: v is bijna de lichtsnelheid, dan zal het omgekeerde
een zeer groot getal worden. Voor v = c wordt γ
zelfs oneindig!
Oefening 13
Als v = 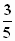 van de
lichtsnelheid c , bereken dan: van de
lichtsnelheid c , bereken dan:
a. 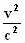
b. 1 – 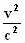
c. 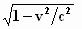
d. γ
We nemen even rust: het is tijd voor de meegebrachte boterhammen.
Terug
|
|
|
|