In my book T&C (pp. 152-153), the following explanation is given of what is meant by true velocity. We assume an object of length ℓ meters between the front point A and the back point A*—that is, frame A in which all clocks are synchronized—is moving relative to another object similarly defined from the front point B to the back point B*—frame B—of the same length ℓ meters and also with synchronized clocks. These two objects (frames) move in opposite directions relative to each other along their length (see Fig 1).  

Ø            The figure shows a timeline diagram in which the objects at a particular point in time are drawn at an angle to each other to show the time advance or delay (bottom line) at a location x along the X-axis from one frame compared to the other.

Of course, because the Lorentz contraction is rejected, the lengths of the systems are equal, regardless of their velocity.

The front point A of system A moves from point B to point B*. The duration of this event is t = ℓ/v sec according to the clock at point B*, so the velocity at which the object moves, according to the observer at B*, is equal to v = ℓ/t m/s.

Figure 1. The dotted lines indicate the positions of the systems at time t = ℓ/v sec—according to the clocks in their respective systems—as seen from the front points. At that time, the front points A₂ and B₂ are γ⁴ ℓ meters apart. The solid lines indicate the positions of the systems at that time t = ℓ/v sec, as seen from the back points. Their mutual distance is consistent with traditional views, but we must remember that these points themselves were γ⁴ ℓ meters apart at the initial time t=0.

The clock at the front point A of the object moving relative to B shows the time t/g sec at that instant, since the clocks in the moving frame A are slower when viewed from frame B (and vice versa).
The end point A* of the object moving relative to B passes—as seen from Q—at that same instant precisely point B. After all, they are of equal length. The clock of A* must then show time t because point B has at that instant travelled exactly the distance ℓ in the frame A.

 However, the clock at A* should also show time t/g sec, because clocks A and A* are synchronized in that frame according to the "observers" in that frame. This is, of course, impossible. This same contradiction also applies to clock B*.

We must conclude that the events at the front and back points of the objects do not occur at the same time, according to the "observers" in that frame. The clocks on an object are synchronized, but the event at the back occurs slightly earlier than the event at the front.
We see that even physical time is a highly subjective quantity. The observer's state of motion relative to the object being observed determines the time regime under which he acts.

 If we observe a moving frame whose "observers" keep their clocks synchronized, the clock further forward in the moving frame will lag behind the clock further back. However, all clocks in the moving frame run at the same speed. From back to front, time progresses in a negative direction.

 We now investigate where the anterior point A, which displayed time t/g when it was at B*, will be located at time t. We therefore consider where A is located when its clock shows the same time as point A* with its synchronized clock. A's time will then have increased by g times.

This point will then have moved a distance of (2g–1)ℓ meters relative to the point where it passed B*. Using the Lorentz factor, this results in a distance of [ℓ+ℓ(v²/c²)] meters.

This result requires some explanation. One is tempted to think that the distance should be g times greater, but one forgets that the distance ℓ was covered by A in less than t sec, namely in t/g sec. His velocity – seen from the other frame – was apparently g times greater. If we take both aspects into account, the distance covered becomes g² times greater. The additional distance covered is then (g²–1)ℓ≈(2g–1)ℓ, provided that (g–1)<<1.

Thus, at time t, point B will also have moved a distance of (2g–1)ℓ meters in the opposite direction on its clock.

At time t sec, points A and B will therefore be at a distance of [ℓ+2(v²/c²)ℓ] meters from each other. We may write this as g⁴ ℓ m.

The velocity that points A and B must attribute to each other is then g⁴ ℓ/t = g⁴ v m/s.

 Two observers in a stationary frame traditionally measure the velocity v of an object moving a distance ℓ from one observer to the other by recording the instant of arrival on the other observer's clock and noting the time difference: t sec. However, by the time the object also exhibits this time t, it has travelled a distance of g⁴ ℓ m.

The result is general: a moving object always has a velocity g ⁴ v  m/s relative to its starting point if we have determined the velocity v in a classical way.

The Lorentz factor here 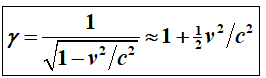represents the time delay due to velocity.
In a gravitational field however, we also experience a time delay. In that case, the Lorentz factor  applies. The time delay in the gravitational field has the same effect on velocity as the time delay due to velocity.  

We may therefore write the actual velocity v* of an object moving in a gravitational field as 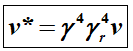  m/s or   – if both g and g_r differ very little from 1 – as the approximation 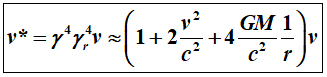 m/sec.

The actual speed is therefore greater than the traditionally formulated speed and therefore differs by:   m/sec.  

Ø            When an object has a speed at an angle j with respect to the line of sight, the actual speed is 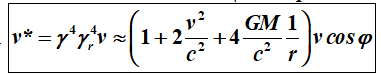    m/sec.

 We will see in §4 that the actual velocity, because of its dependence on the distance r   (in the term )   from the Sun, also involves an additional acceleration which plays an important role in solving the mysterious acceleration of the Pioneers.

To Obstruction Theory

 Back