To
Contents
To Homepage
To
Part 7 Comet Oumuamua
To
Part 8b Angle Effect
8a
Calculations on Comet Oumuamua
To
accurately calculate the angular effect, we need to know the angle of the
orbital motion at each location relative to the direction of the Sun.
However,
this proves to be a difficult and time-consuming task, so we limit ourselves
to making an estimate, while recognizing that the results are sensitive to the
accuracy of the estimate. We prefer to leave definitive calculations to
experienced astronomers.
The
Optical Distance Effect
The
velocity at which Oumuamua moved toward the solar system is practically equal
to the velocity at which the comet eventually moves away from the solar
system. According to astronomers' calculations, this base velocity was 26.33
x 103 m/s. This allows the velocity at distance r relative to
the sun to be calculated using the traditional formula
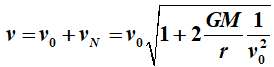m/sec.
This
doesn't yet take into account the very small change in velocity due to the
changed geometric position.
If
the comet's orbital velocity away from
the Sun is v m/s and the angle of this velocity with the heliocentric
distance is j
, then the radial velocity vrad
= vcosj
m/s. See Fig 5 on
the right. The angle j
is then greater than 90o.
Then the optical distance to the sun is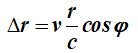 
meters smaller than according to Newton. The Sun's gravitational
acceleration is therefore greater. The comet is therefore slowed down more by
the sun and retains less speed over time than according to traditional theory.
The difference in gravitational acceleration as we move away from the Sun
between points that have a distance difference of Dr
meters towards the Sun is found by
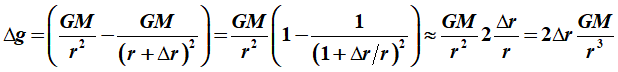m/s2.
With
the optical distance difference 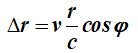meters
this
becomes
m/s2.
The
component of this acceleration in the direction of the orbital motion gives us
the result that the comet is slowed down more in its speed than
according to traditional theory with the value:
m/s2.
We would like to integrate this expression over the distance from
perihelion to an arbitrary point, but this is difficult because the velocity v
and the cosj
both depend on the distance r.
We therefore approach this problem numerically
by introducing an estimated average value for cosj
between two consecutive points, whose distance and velocity are known, and
using the product of the average additional acceleration Dg
between the points, the time duration, and the value of cosj
to calculate the difference in velocity between the two points. In this way we
can get a reasonable idea of the speed decrease over a long
distance by adding up the speed differences over the intermediate points.
In Table
2, column H
shows the speed deceleration caused
by the optical distance difference. Multiplied by the time period in column G
and divided by sinj
because the comet goes through the distances at an angle, column I
shows the smaller decrease in velocity compared to Newton's at various
distances from the Sun. Column J
shows the sum of the decreased speed at various distances.
This
determines the magnitude of the optical distance effect for this estimate of j.
The following data were used in the calculations
for Oumuamua
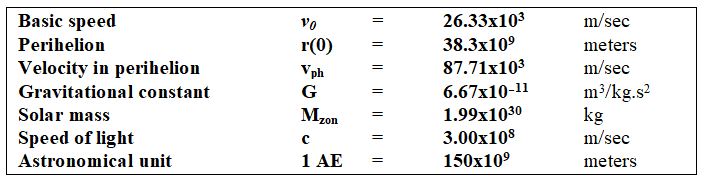
This gives:
Table
2: The difference in speed between the obstruction theory and Newton's theory
due to the optical distance difference. The comet is losing speed.
Back
To
Part 8b Angle Effect
