ž
4 De relatie tussen de vier co÷rdinaten
die we verkrijgen uit
ruimte en tijdmetingen.
Een analytische uitdrukking voor het
zwaartekrachtveld.
Het
is in deze verhandeling niet mijn bedoeling de algemene
relativiteitstheorie zo formeel mogelijk met een minimum
aan axioma's te presenteren. Het is juist mijn streven de theorie zo
uit de doeken te doen dat de lezer zelf ervaart hoe van zelfsprekend
en natuurlijk de ingeslagen weg is en dat de vˇˇronderstellingen
die het fundament er van vormen in hoge mate aansluiten bij wat
we al weten.
In die zin voer ik de volgende twee vˇˇronderstelling in:
* Voor
een oneindig klein vierdimensionaal gebied is de speciale
relativiteitstheorie bij
een geschikte co÷rdinatenkeuze altijd geldig.
De toestand van versnelling van het oneindig
kleine ("lokale") co÷rdinatenstelsel moet hierbij zo worden gekozen, dat er geen
zwaartekrachtveld optreedt; dat is voor een oneindig klein gebied altijd
mogelijk. De ruimtelijke co÷rdinaten zijn X1 , X2
, X3 en de
bijbehorende, met een geschikte klok gemeten, tijdco÷rdinaat is X4.
Opmerking van Einstein:
"De eenheid van tijd moet zo worden gekozen dat de lichtsnelheid
in vacuŘm
ľ gemeten in het "lokale" co÷rdinatenstelsel ľ
gelijk wordt aan 1"
Deze
co÷rdinaten hebben, indien we ons daarbij in gedachten ook een
onbuigzaam en recht staafje als eenheidsmeetlat voorstellen, bij een
gegeven oriŰntering van het co÷rdinatenstelsel een directe
natuurkundige betekenis in de zin van de speciale
relativiteitstheorie. Namelijk: de uitdrukking
(1) ds 2
= ľ dX1 2 ľ dX2
2 ľ dX3 2 + dX4 2
heeft dan volgens de speciale relativiteitstheorie
een door ruimteľ en tijdmetingen verkregen waarde die
onafhankelijk is van hoe het lokale co÷rdinatenstelsel wordt georiŰnteerd.
We noemen ds de grootte van het "lijnelement" tussen twee oneindig
dicht bijeen staande punten in de vierdimensionale ruimte.
Als de bij het element (dX1 ů.. dX4) behorende ds
2 positief is, dan noemen we in navolging van Minkowski ds
2 tijdachtig en in het tegenovergestelde
geval ruimteachtig.
Bij
het beschouwde "lijnelement", of bij de twee
oneindig dicht bij elkaar staande puntgebeurtenissen, behoren ook
zekere differentialen
dx1ůůdx4
van de vierdimensionale co÷rdinaten
van een gekozen referentiestelsel. Als deze differentialen, evenals
een eerder genoemd "lokaal" stelsel, voor de
beschouwde plaats zijn gegeven, dan
kunnen de dXν
door zekere lineaire,
homogene uitdrukkingen van de differentialen dxσ
worden voorgesteld:
(2)
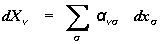
(3)
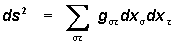
waarbij de elementen gστ
functies van de xσ
zullen zijn, die niet meer van de oriŰntatie en de bewegingstoestand
van het "lokale" co÷rdinatenstelsel kunnen afhangen.
Immers, de waarde ds 2 , die behoort bij de beschouwde,
in de ruimteľtijd oneindig dicht bijeen liggende
puntgebeurtenissen, heeft een grootte die te vinden is met meetlatten
en klokken, die niet afhangt van welke specifieke co÷rdinatenkeuze dan ook. We nemen aan
dat voor de gστ
geldt dat gστ
= gτσ . De sommatie strekt zich
uit over alle waarden van σ
en τ, zodat de totale som uit 4 x 4 sommaties bestaat,
waarvan er 12 paarsgewijs gelijk zijn.
Uit deze beschouwingswijze
vinden we de speciale relativiteitstheorie terug als het , op grond
van de specifieke eigenschappen van de gστ
in een eindig gebied ,
mogelijk is het referentiesysteem voor dit gebied zo kiezen dat
de gστ
de volgende constante
waarden aannemen.
(4)
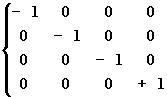
We zullen later zien dat voor eindige gebieden de keuze van een
dergelijke co÷rdinatenstelsel in het algemeen niet
mogelijk is.
Uit de beschouwingen van ž 2
en ž 3 blijkt dat de grootheden gστ
vanuit natuurkundig standpunt als die grootheden moeten worden
beschouwd die het zwaartekrachtveld met betrekking tot het gekozen
referentiesysteem beschrijven. Als we namelijk om te beginnen eens
aannemen dat voor een zeker vierdimensionaal gebied bij de
keuze van geschikte co÷rdinaten de speciale relativiteitstheorie
geldig is, dan hebben de gστ de in (4) gegeven waarden. Een
geheel aan zichzelf overgelaten stoffelijk punt beweegt zich dan met
betrekking tot dit stelsel eenparig en rechtlijnig.
Wanneer men nu door een willekeurige substitutie overgaat op
nieuwe ruimteľtijdľco÷rdinaten
x1 ů.. x4 , dan zullen in dit
nieuwe stelsel de gμτ
geen constanten, maar
functies van ruimte en tijd
zijn. Tegelijkertijd zal de beweging van het vrije massapunt in
dit nieuwe co÷rdinatenstelsel in het algemeen kromlijnige en niet
eenparige zijn, waarbij de wet waaraan de beweging moet
voldoen onafhankelijk is van de stoffelijke samenstelling van
het bewegende massapunt. We zullen deze beweging dus moeten uitleggen als een
beweging onder invloed van een zwaartekrachtveld. Samenhangend met een
ruimteľtijd afhankelijkheid van de gστ
nemen we dus het optreden van een zwaartekrachtveld waar. Ook
in het algemene geval waarbij we de geldigheid van de
speciale relativiteitstheorie niet in een eindig gebied door een
passende keuze van het co÷rdinatenstelsel kunnen bewerkstelligen,
zullen we
moeten blijven vasthouden
aan het uitgangspunt dat de gστ
het zwaartekrachtveld beschrijven.
De
zwaartekracht neemt dus volgens de algemene relativiteitstheorie een
uitzonderlijke rol in naast de overige krachten, in het bijzonder de
elektromagnetische krachten, aangezien de 10
functies gστ die het zwaartekrachtveld
beschrijven tegelijkertijd de metrische eigenschappen van de
vierdimensionale meetbare
ruimte bepalen.
Terug
