Naar Uitleg §2 Balken  
Naar Uitleg Inleiding  
Naar Vertaling § 1 Klokken
Naar Centrale Hal  

Wie er wel eens over heeft nagedacht wat "tijd" voor een eigenaardig natuurkundig begrip is (niet tastbaar, loopt maar door, géén materiaaleigenschap), kan in een sombere verwarring raken en uit geestesnood zijn klokje prijzen dat tenminste de juiste "tijd" aanwijst, dat geeft enig houvast. Einstein schudt je echter wakker met de opmerking dat we nooit goed hebben afgesproken wat "tijd" precies is. 
"Dat wordt dan toch langzamerhand eens tijd!", proberen we grappig te zijn.
Over "tijd"  kan vanuit de natuurkunde alleen worden gesproken als de "tijd" kan worden gemeten. Daarom geeft Einstein in deze eerste paragraaf  een nauwkeurig recept voor het meten van "tijd". Onze huidige kennis van de tijd sluit daar geheel bij aan: iedereen weet dat de ster die je ‘s nachts ziet er uitziet zoals hij er vele jaren geleden uitzag (zie: oefening 3). Je kan zelfs naar een ster kijken en je afvragen of deze niet op ditzelfde moment een supernova wordt. Dat weet je niet, dat zal je waarschijnlijk nooit weten omdat het te lang duurt voor het licht van die veronderstelde ontploffing bij ons is. Een tweede vraag die daarop aansluit, is nog verwarrender: "Is dit moment eigenlijk ook wel ditzelfde moment bij die ster?" Dat zijn ongrijpbare gedachten die te maken hebben met "gelijktijdigheid".

    Oefening 3: Hoe oud is het laatste nieuws

Mocht je plotseling een lichtflits op de maan zien, dan heeft deze ruim één seconde eerder plaatsgevonden: je deelt de afstand (in km) door de lichtsnelheid (in km per seconde) en je krijgt het tijdsverschil Δt:                                     Bereken zelf voor de zon, als daar een heftige zonnevlam optreedt, hoe oud deze is op het moment dat hij hier wordt waargenomen. De afstand tot de zon is afgerond en gemiddeld: 149,6 miljoen kilometer. (Antwoord: ). Als u een supernova waarneemt in een sterrenstelsel dat zich op een afstand van 65 miljoen lichtjaar bevindt, hoelang geleden……… Dit is een grapje, u weet natuurlijk allang dat astronomen de afstand in tijd uitdrukken, dus het antwoord is gewoon 65 miljoen jaar.

Einstein wilde aangeven hoe je de gelijktijdigheid van twee gebeurtenissen bepaalt. Daar heb je klokken voor nodig die gelijklopen, waarmee hij bedoelt: klokken die even snel lopen en voortdurend dezelfde tijd aanwijzen. Hij ontwierp daarom een meetprocedure om vast te stellen of twee klokken gelijklopen, zelfs als deze zeer ver van elkaar verwijderd zijn. Van het resultaat zullen wij niet paf staan, want je weet dat als je een gebeurtenis op een ver verwijderde plek waarneemt, de gebeurtenis eerder heeft plaatsgevonden, en wel zoveel eerder als het licht nodig heeft om je te bereiken. Je hoeft alleen maar de afstand te kennen en door terug te rekenen, kan je precies vertellen op welk tijdstip de gebeurtenis plaatsvond. Een eventuele klok die bij de gebeurtenis stond, zou die tijd hebben moeten aangeven van de gebeurtenis anders liep die klok niet gelijk ("met onze klokken", denken we er dan bij). Dat is deel 1 van het verhaal. Niks bijzonders, …… tot de klokken meebewegen in een voorbijvliegend stelsel. Dat is een ander verhaal.

We zullen de gedachtegang van Einstein volgen, alleen al omdat het een onverwacht idioot gedoe is met klokken en bewegende voorwerpen. In de volgende paragrafen zullen de klokken ons  om de oren vliegen. Let er ondertussen eens op, via de vertaling, hoe zorgvuldig Einstein zijn theorie heeft opgezet: helder, zonder overbodige uitweidingen.

Einstein gaat uit van een coördinatenstelsel. Dat woord "coördinatenstelsel" schreeuwt om een toelichting! Die komt nu.
Om aan te geven waar een voorwerp zich bevindt, moet je duidelijk maken waar het zich bevindt ten opzichte van andere voorwerpen, die op een bekende plaats staan.
Op de dwingende vraag van een dief: "Waar ligt jouw geld!", antwoord ik: "Rechts achterin de bovenste la van de kast op de gang op de eerste verdieping vindt u mijn spaargeld onder het stapeltje zakdoeken". Ik vertel in de praktijk niet alleen waar de buit ligt, maar ook nog hoe je er komt.

In de natuurkunde is het eveneens gebruikelijk de plaats van een voorwerp op een niet voor tweeërlei uitleg vatbare manier aan te geven (maar zonder de weg te wijzen) namelijk via het coördinatenstelsel!

We kiezen een vast punt (dat mag gunstig worden uitgekozen) en geven dat aan met het symbool O (van het woord Oorsprong) en trekken vanuit dat punt drie loodrecht op elkaar staande lijnen. Bij het bepalen van de plaats in een ruimte worden meestal twee loodrecht op elkaar staande lijnen in een verticaal vlak getekend waarvan er één horizontaal loopt, de x - as en de ander verticaal, de y - as. Loodrecht op het snijpunt van die twee lijnen wordt één horizontale lijn getekend, de z - as (zie figuur 1.01).  De gestreepte delen van de assen worden negatief genoemd en de doorgetrokken delen zijn de positieve x–as, de positieve y–as en de positieve z–as. Langs die assen denken we ons afstandsstrepen zoals op een liniaal. Van ieder punt in de ruimte kan je loodlijnen (de vette gestreepte lijnen) neerlaten op de drie assen. Waar zo'n loodlijn de as treft, kan de x–, y– of z–waarde worden afgelezen (positieve of negatieve waarden). De andere lijnen in de figuur zijn bedoeld om de vlakken te vinden die loodrecht op de assen staan en door het punt gaan. Iedere lijn in zo'n vlak staat loodrecht op de betreffende as.
Die drie afstanden op de assen vormen de coördinaten van het punt in dat assenstelsel..

Een dergelijk systeem wordt een cartesisch¹⁾ coördinatenstelsel genoemd of kortweg een "assenstelsel".

In een huis kan je nu de plaats aangeven door bijvoorbeeld, voor de woning staande, op de grond bij de voordeur de oorsprong O te kiezen, de positieve x-as loopt langs de voorgevel naar rechts, de positieve y-as loopt omhoog en de negatieve z-as loopt de woning in. Van ieder punt in de woning ligt dan vast hoe ver naar links of naar rechts het zich bevindt ten opzichte van de voordeur en hoe hoog  en hoe  diep (bij onze keuze een negatieve waarde) het zich in de woning bevindt. De drie getallen vormen de coördinaten. Ik had de dief dus ook kunnen zeggen: "Mijn spaargeld bevindt zich, gerekend vanaf uw lompe voeten, op de plaats met de coördinaten (2,3,-4), met als eenheid de meter", maar dat zou geen verstandig antwoord zijn geweest.

Ø De oorsprong O is het punt met de waarden (0, 0, 0) en wordt vaak het nulpunt genoemd.

Het assenstelsel denken we ons als een onvervormbaar geheel. Als het huis in de winter door de lage temperatuur een millimeter is gekrompen, willen we niet dat ons assenstelsel meekrimpt. Dan zouden we de krimp niet kunnen meten. De assen zijn dus starre, loodrechte lijnen. En ook de voorwerpen waar we in de bewegingsleer mee werken, beschouwen we als onvervormbaar. Daar wijst Einstein op in de laatste regels van zijn inleiding (p.892) omdat hij zal laten zien dat aan die onvervormbaarheid nog wel wat af te dingen is.

    Fig. 1.01 Een cartesisch coördinatenstelsel

Bij een coördinatenstelsel denk je in eerste instantie aan een stilstaand stelsel. Daarmee leg je vast waar een eveneens stilstaand voorwerp zich bevindt. Maar een voorwerp kan ook in beweging zijn. Dan veranderen de coördinaten van het voorwerp voortdurend en we zeggen dan dat het voorwerp een baan in het stelsel-in-rust beschrijft. Je mag  met het voorwerp ook een coördinatenstelsel laten meebewegen. Dan is het voorwerp in dat meebewegende stelsel gewoon weer in rust.

"Rust" is een beladen begrip. Einstein maakt ons op p. 892 duidelijk dat we het begrip "een ruimte in absolute rust" uit ons woordenboek kunnen schrappen. Wat moeten we ons dan voorstellen bij: een assenstelsel-in-rust?

Dat is gewoon een afspraak. Een coördinatenstelsel waarin wij ons tezamen met onze omgeving in rust bevinden, noemen we het coördinatenstelsel in "rust" ondanks dat we ondertussen best weten  dat we met de hele mikmak met een gigantische snelheid rond de zon draaien.

In zo’n coördinatenstelsel-in-rust gelden de wetten van   Newton ²⁾  . Daar verwijst Einstein naar in de eerste alinea van §1. Het gaat om de mechanicawetten die op de middelbare school worden geleerd, te weten:

· op een voorwerp dat stilstaat of volhardt in een eenparige (= constante) rechtlijnige beweging werken geen krachten of de krachten houden elkaar in evenwicht ,

· als een voorwerp vanwege één overgebleven kracht een versnelling ondergaat, geldt dat de versnelling a gelijk is aan de kracht F gedeeld door de massa m van het voorwerp (of a = F/m meestal geschreven als F = m.a)

De "euclidische meetkunde" waarover Einstein spreekt, is de gewone meetkunde zoals je die op school hebt geleerd. Niets bijzonders.

Voor de beschrijving van een bewegend punt moet de plaats op ieder tijdstip met een formule, een functie, kunnen worden vastgesteld, "als functie van de tijd".

Voorbeeld:
De plaats op het tijdstip t van een eenparige beweging langs de X-as kan worden beschreven met de formule ("functie van de tijd"):
                     x(t) = x(0) + v. t

"Als functie van de tijd"; zo kan je dus elke beweging beschrijven, maar daar zat juist de makke! Het begrip "tijd" rammelde.

Einstein begint p. 893 met een belangrijke opmerking, namelijk dat tijd voor ons altijd te maken heeft met gelijktijdigheid. Daarbij houdt hij zich niet bezig met gezanik: hoe je precies de gelijktijdigheid moet bepalen van twee gebeurtenissen waar je zelf bijstaat, daar wil hij niet op ingaan. Dat spreekt voor zich. In de voetnoot doet hij dat af met de woorden dat dit probleem "via een abstrahering moet worden aangepakt". Dat is mooi gezegd en het betekent dat het eveneens  theoretisch kan worden uitgewerkt. De meetnauwkeurigheid van de instrumenten zal daarbij een belangrijke rol spelen. Voor ons verhaal is dit verder niet van belang.

Waar het om gaat, is dat we de tijd aangeven aan de hand van een gelijktijdige gebeurtenis. Bijvoorbeeld het jaar 79 na Christus (toen werd Pompeï bedolven) was het jaar dat de aarde 1926 rondjes rond de zon minder had afgelegd dan nu (2005). Het rondje waar de aarde mee bezig was en de uitbraak van de Vesuvius vielen samen: twee gelijktijdige gebeurtenissen.

De definitie vraagt om een verfijning als het om gebeurtenissen gaat die zich in het 'nu' op ver van elkaar verwijderde plaatsen afspelen. Is "gelijktijdig" dan het moment dat je er bericht van krijgt of het moment dat het werkelijk gebeurde. We kiezen uiteraard voor het laatste. Als er op de planeet Mars iets gebeurt, weten wij er pas na minimaal 4 minuten en 20 seconden van (als Mars op zijn dichtstbijzijnde punt van de aarde is), maar het kan ook 21 minuten duren als Mars aan de andere kant van de zon staat, het verst verwijderde punt ten opzichte van ons. Je moet dus van moment tot moment de afstand kennen om het tijdstip van de gebeurtenis te kunnen bepalen. Of, wat veel handiger is, je zet een waarnemer (een instrument of desnoods een journalist) op Mars met een klok die precies gelijkloopt met de klokken op aarde. Dan kan hij van elke gebeurtenis doorbellen hoe laat deze plaatsvond.

Het is van het grootste belang om goed te omschrijven hoe twee klokken op grote afstand van elkaar gelijk kunnen worden gezet. De meetmethode die Einstein aangeeft, gaat zo: hij geeft een waarnemer in punt A een klok en een andere waarnemer die zich in het punt B bevindt, een identieke klok, die precies even snel loopt, maar ze hoeven niet dezelfde tijd aan te wijzen. De klokken zijn ver van elkaar verwijderd, zodat van een gebeurtenis slechts een "A–tijd" kan worden vastgesteld en een "B–tijd", zoals bovenaan p.894 in het document staat. Er moet worden gecommuniceerd tussen beide waarnemers.

A en B verkeren ten opzichte van elkaar in rust. De ruimte tussen A naar B is leeg (een gewaagde veronderstelling, want iedereen dacht toen nog dat de ruimte gevuld was met "lichtether"!). Tussen A en B kan een lichtstraal heen en weer worden gezonden. Terug gaat gewoon door terugkaatsing. De afstand heen is dezelfde als terug. Volgens de 2^de aanname (zie §0 p.10) beweegt het licht even snel op de heenweg als op de terugweg. Het licht doet dus even lang over de heenweg als over de terugweg. Hij noemt het tijdstip dat het lichtsignaal uit A vertrekt t_A en het moment dat het signaal bij B tegen het spiegeltje kaatst t_B . De tijd die het licht erover doet om van A naar B te gaan is dus t_B–t_A. Het signaal vertrekt door terugkaatsing op hetzelfde tijdstip t_B uit B en komt op tijdstip t΄_A aan in A. Het accent staat erbij om de twee tijdstippen, vertrek en aankomst, in A te kunnen onderscheiden.

Einstein zegt nu dat de klokken gelijklopen als de tijdsduur over de heenweg gelijk is aan de tijdsduur over de terugweg:   t_B – t_{A  =}   t'_A – t_B

Dat gaan we controleren (oefening 4)

Oefening 4: Waarom lopen de klokken gelijk

Als je twee klokken op twee verschillende plaatsen kan laten gelijklopen en als de methode "geen tegenstrijdigheden bevat", waarmee gezegd wil zijn dat we hopen dat niet uit onverwachte hoek blijkt dat het niet klopt, dan kan je ook veel klokken op veel verschillende plaatsen gelijk laten lopen en die lopen logischerwijs ook allemaal onderling gelijk.(Dat slaat op de logische formulering: Als A gelijk met B en C, dan ook B en C gelijk).

Onderaan deze bladzijde memoreert Einstein dat de lichtsnelheid c wordt voorgesteld door: tweemaal de afstand tussen A en B te delen door de tijd die het licht erover doet om van A naar B en weer terug te gaan. Met de streep boven AB , dus 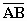, wordt aangegeven dat het om de afstand van A naar B gaat.

Op deze wijze heeft Einstein aangegeven hoe je de "tijd" voor de gebeurtenissen in één coördinatenstelsel-in-rust kan vaststellen. Hij noemt dit op p. 895 essentieel. Door op die manier de "tijd" te meten, krijgt de "tijd" een betere natuurkundige betekenis. Ieder weldenkend mens zal toegeven dat, bij acceptatie van de meetmethode, men niet snel ruzie zal krijgen over het tijdstip van een gebeurtenis in een verafgelegen plaats, mits die plaats in rust is ten opzichte van jou zelf. Het is wat omslachtig, maar het is misschien wel de enige manier om de juiste tijd op een verafgelegen plaats te bepalen. Of "dit moment" hier hetzelfde is als "dit moment" op een verafgelegen plaats, kunnen we dan met "ja" beantwoorden als het tijdstip hier overeenkomt met het tijdstip daar.

Let echter op: we laten ons nog niet uit over de tijd in een stelsel-in-beweging en daarmee bedoelen we de tijd in een bewegend stelsel dat beschouwd wordt vanuit het stelsel-in-rust. In de volgende paragraaf komt dat aan de orde. 
Je moet daarbij bedenken dat, omdat er geen "ruimte in absolute rust" is "de tijd in het stelsel-in-rust beschouwd vanuit het stelsel-in-beweging" op hetzelfde neerkomt als "de tijd in het stelsel-in-beweging beschouwd vanuit het stelsel-in-rust" en dat "de tijd in het stelsel-in-rust bezien in het stelsel-in-rust" weer op hetzelfde neerkomt als "de tijd in het stelsel-in-beweging bezien vanuit het stelsel-in-beweging". Die dingen zijn verwisselbaar. 

Terug

Naar  1) Genoemd naar de Franse wiskundige, filosoof en wetenschapper René du Perron Descartes (1596 - 1650)           
2) Sir Isaac Newton, geboren in 1642 in Lincolnshire en overleden in 1727 (Londen?)

Antwoorden: Oefening 3: 499 seconden
                    Oefening 4:  1 minuut en 7 seconden terugzetten