|
I. Het kinematisch gedeelte
§ 1. De definitie van de gelijktijdigheid.
We gaan uit van een
coördinatenstelsel waarin de mechanicawetten van Newton gelden. We noemen
dit coördinatenstelsel het "stelsel-in-rust" om het in
woorden te kunnen onderscheiden van de later in te voeren andere
coördinatenstelsels en om de opgevoerde denkbeelden te kunnen preciseren.
Indien
een materieel punt in dit coördinatenstelsel stilstaat, kan zijn plaats ten
opzichte van dit stelsel, gebruikmakend van de methoden van de euclidische
meetkunde, met behulp van onvervormbare meetlatten worden bepaald en de
plaats kan in cartesische coördinaten worden uitgedrukt.
Als
we de beweging van een massapunt willen beschrijven, moeten de
waarden van zijn coördinaten als een functie van de tijd bekend zijn. Men
dient zich nu te realiseren dat een dergelijke wiskundige beschrijving pas
een natuurkundige betekenis heeft, als het voor iedereen van begin af aan
duidelijk is wat hier onder "tijd" moet worden verstaan. We
moeten ons realiseren dat al onze uitspraken, waarin de tijd een rol speelt,
altijd uitspraken over gelijktijdige gebeurtenissen zijn. Als
ik bijv. zeg: "Die trein komt hier om 7 uur aan," dan wil dat
zoiets zeggen als: "Het aanwijzen van de 7 door de kleine wijzer van
mijn klok en de aankomst van de trein zijn gelijktijdige
gebeurtenissen." 1)
Men
zou kunnen denken dat alle problemen betreffende de definitie van de
"tijd" opgelost zijn door in plaats van de "tijd"
de "aanwijzing van mijn klok" te gebruiken. Die definitie
zou inderdaad voldoende zijn als het er uitsluitend om zou gaan een tijd te
definiëren voor de plaats waar de klok zich dan bevindt; de definitie
voldoet echter niet meer zodra het er om gaat aan gebeurtenissen, die zich
op zeer verschillende plaatsen afspelen, een "tijdvolgorde" te
koppelen, of – wat op hetzelfde neerkomt – aan gebeurtenissen, die zich
op ver van de klok gelegen plaatsen afspelen, tijdstippen toe te kennen.
We
zouden er weliswaar genoegen mee kunnen nemen aan een gebeurtenis een
tijdstip te koppelen door in de oorsprong van het coördinatenstelsel naast
de klok een waarnemer te plaatsen, die bij iedere gebeurtenis waarvan de
tijd moet worden vastgesteld, en waarvan hij via een lichtsignaal door de
lege ruimte op de hoogte wordt gebracht, de bijbehorende stand van de klok
noteert. Het op die manier toekennen van de tijd leidt echter tot de
ongewenste situatie dat de tijdwaarneming niet helemaal onafhankelijk is van
de opvatting van degene die over de klok gaat, zoals we uit ervaring weten.
De volgende beschouwing leidt tot een veel bruikbaardere methode om de tijd
vast te stellen.
Als
zich in het punt A van de ruimte een klok bevindt, dan kan een
waarnemer die zich ook in A bevindt aan de gebeurtenissen in
de directe omgeving van A een tijd toekennen door gelijktijdig
met deze gebeurtenissen de stand van de klok af te lezen. Als zich in het
punt B van de ruimte ook een klok bevindt – uiteraard
"een klok met precies dezelfde eigenschappen als die in A"
– dan is het toekennen van een tijdstip aan een gebeurtenis in de directe
omgeving van B
door een zich in B bevindende waarnemer eveneens mogelijk. Het
is echter niet mogelijk de tijd van een gebeurtenis in A
zondermeer met de tijd van een gebeurtenis in B te
vergelijken; we hebben tot nu toe slechts een "A-tijd"
en een "B-tijd" gedefinieerd, maar geen "tijd"
die zowel voor A als voor B geldig is. Deze
laatste "tijd" kan echter worden gedefinieerd als
men per definitie vastlegt dat de "tijd"
die het licht nodig heeft om van A naar B te
gaan gelijk is aan de "tijd" die het licht nodig
heeft om van B naar A te gaan. Als namelijk een
lichtstraal op de "A-tijd" tA van A
naar B gaat en daar op de "B-tijd" tB
in B wordt teruggekaatst naar A om op de
"A-tijd" t’A weer A te
bereiken, dan kunnen we zeggen dat de beide klokken volgens de definitie
gelijklopen als:
tB – tA
= t’A – tB .
We nemen aan dat deze
definitie voor het gelijklopen van klokken geen tegenstrijdigheden bevat en
op willekeurig veel punten kan worden betrokken, zodat dus voor alle punten A,
B en C de volgende relaties gelden:
1.
Indien de klok in B gelijkloopt met de klok in A,
dan loopt de klok in A gelijk met de klok in B.
2.
Indien de klok in A zowel met de klok in B als
met de klok in C gelijkloopt, dan lopen ook de klokken in B
en C gelijk met elkaar.
Op
deze wijze hebben we dankzij enig (abstract) natuurkundig inzicht vastgelegd
wat onder gelijklopende klokken-in-rust, die zich op verschillende plaatsen
bevinden, moet worden verstaan en daarmee hebben we kennelijk een definitie
voor "gelijktijdigheid" en een definitie voor "tijd"
gevonden. De "tijd" van een gebeurtenis is de met de
gebeurtenis gelijktijdige tijdsaanduiding op een klok, die zich in rust op
de plaats van de gebeurtenis bevindt, en die voor alle tijdsbepalingen, die
met de genoemde klok worden gedaan, gelijkloopt met een zekere andere klok–in–rust.
We
stellen tenslotte nog vast dat volgens de ondervinding de grootheid
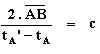
een universele constante is (de
lichtsnelheid in de lege ruimte).
Waar
het om gaat, is dat we de tijd door middel van klokken-in-rust in
het stelsel-in-rust hebben
gedefinieerd; we noemen de zojuist gedefinieerde tijd die betrekking heeft
op het stelsel-in-rust: "de tijd van het stelsel-in-rust"
Voetnoot:
1) De
onnauwkeurigheid die in het begrip gelijktijdigheid schuilt van twee
gebeurtenissen op (ongeveer) dezelfde plaats en die we eveneens via een
abstrahering kunnen aanpakken, zal hier niet worden besproken.
|