Tweelingparadox

De Tweelingparadox
uitgelegd door Albert Einstein zelf

Naar Entree
Naar E = m c²

Voorwoord
Henk Dorrestijn

Kort gezegd komt de tweelingparadox hierop neer dat je van twee precies even oude personen, bijvoorbeeld twee tweelingbroers, er één in een ruimtetoestel met grote snelheid naar een nabije ster stuurt, om laat draaien en weer terug laat komen. Tijdens de perioden van grote snelheid zal zijn tijd trager lopen en bij terugkomst zal hij jonger zijn dan zijn achtergebleven tweelingbroer. Maar, het relativiteitsprincipe zegt dat je de beweging net zo goed vanuit het ruimtevaartuig kan beschrijven. Vanuit het ruimtevaartuig gezien, verkrijgt de achtergebleven tweelingbroer de grote snelheid waardoor diens tijd trager loopt. Bij terugkomst moet, volgens de broer die in het ruimtevaartuig zat, zijn tweelingbroer juist jonger zijn. Ze zouden allebei jonger zijn dan de ander, wat gewoon volgens de logica een onmogelijkheid is. Dat is de paradox! Een schijnbare tegenstrijdigheid, want bij nadere beschouwing blijkt de laatste redenering - de thuisgebleven broer moet ook jonger zijn dan zijn heldhaftige broer - niet klopt.

Voor 1920 werd dit gedachte–experiment regelmatig aangevoerd als argument tegen de geldigheid van de (speciale) relativiteitstheorie. Het is een intrigerend en moeilijk gedachte–experiment dat tot de dag van vandaag tot discussie leidt. De verklaring die ervoor wordt gegeven, is meestal onjuist omdat slechts wordt bewezen waarom de ruimtevaarder jonger is gebleven dan zijn minder avontuurlijke broer. Dit gaat soms gepaard met halsbrekende toeren voor de ruimtevaarder om onderweg - bij een snelheid van halverwege de lichtsnelheid - plotseling van het ene in het andere ruimteschip te springen. Dan is het geen paradox meer, maar een godswonder dat de waaghals nog leeft! Het wordt begrepen alsof de paradox zit in het feit dat de ruimtevaarder bij terugkomst minder oud is dan zijn achtergebleven broer, zonder vanuit het relativiteitsbeginsel te begrijpen dat de ruimtevaarder ook zou kunnen zeggen dat zijn broer jonger is gebleven. Het is weliswaar, zoals Einstein in het volgende artikel door zijn criticus laat zeggen: ".... zacht gezegd eigenaardig te noemen", maar niet meer dan dat. Wanneer je het daarbij laat, wordt de tweelingparadox van zijn paradoxale karakter ontdaan en tot een "simpel" probleem teruggebracht! Zelfs de beroemde Richard Feynman in The Feynman Lectures on Physics vol I blz. 16–3 bezondigt zich hieraan. Jammer, want de echte paradox, die in de "Dialoog over de bezwaren die tegen de relativiteitstheorie worden ingebracht" door Einstein wordt weerlegd, is veel spannender dan wat veelal onder de naam "Tweelingparadox" wordt verkocht.

Wat zegt Einstein erover. Het probleem werd toen nog de klokkenparadox genoemd. Zoals je zult merken, is de wijze waarop hij de paradox ontzenuwt een zeer verhelderende les in de natuurkunde. Het blijkt dat er een gedachtefout wordt gemaakt door beide stelsels gelijkwaardig te noemen, terwijl het stelsel van de ruimtevaarder versneld en vertraagd wordt en dat van zijn broer niet. Voor de werkelijke verklaring heeft hij een stukje van de algemene relativiteitstheorie nodig. Dan blijkt pas waarom slechts de vertrokken en heelhuids teruggekeerde tweelingbroer jonger is dan zijn achtergebleven broer.

Einstein schreef zijn verklaring in de vorm van een dialoog, geïnspireerd door Galileo Galileï's "Dialoog over de twee belangrijkste wereldstelsels" uit 1630. Bij de Engelstalige heruitgave in 1953 schreef Einstein hiervoor het voorwoord. Maar dat is van latere datum. Toen hij in 1918 zijn "Dialoog" schreef, had hij al regelmatig te maken met achterbakse aanvallen op zijn werk waarbij men hem van plagiaat beschuldigde en tegelijkertijd zijn theorie probeerde onderuit te halen. Dit zou nog enige jaren doorgaan, culminerend in de Bad Nauheim discussies in 1920, waar zich onder zijn critici een groep bevond die zich liet leiden door uitgesproken antisemitische gevoelens.

In de verdediging van de theorie legt Einstein een grote strijdvaardigheid aan de dag. Hij verheldert op een geweldige manier de natuurkundige verklaring van de klokkenparadox en zet "en passant" zijn critici te kijk.

Het artikel werd geschreven nadat Einstein de Algemene Relativiteitstheorie in een eindvorm had gegoten. Zoals al eerder werd gesteld (zie de uitleg bij § 4 van het artikel over de speciale relativiteitstheorie) kon Einstein pas een verklaring geven voor het achterlopen van de klok die een ommetje had gemaakt met behulp van de Algemene Relativiteitstheorie, maar hij was er in 1905 al van overtuigd dat de thuisblijvende klok voor zou lopen op de andere. Pure fysische intuïtie.

Dit artikel is zondermeer een literaire poging te noemen. Wie alleen de kern van het verhaal, het weerleggen van de paradox, wil bekijken, moet het gedeelte tussen de twee groene lijnen lezen, maar de rest van het verhaal is eveneens boeiend.

Het originele artikel:
Albert Einstein: Dialog über Einwände gegen die Relativitätstheorie; Die Naturwissenschaften; zesde jaargang 29 november 1918 p.697–702

Dialoog over de bezwaren die tegen de relativiteitstheorie worden ingebracht

door Prof. Dr. A. Einstein, Berlijn

Vertaling Henk Dorrestijn

De criticus:
Wij critici hebben al zo vaak door middel van tijdschriftartikelen bezwaren van uiteenlopende aard tegen de relativiteitstheorie onder woorden gebracht maar jullie relativisten ¹) nemen niet eens de moeite hierop te antwoorden. Ik wil niet ingaan op de vraag of het arrogantie, lafheid of geestelijke luiheid is die aan deze laksheid ten grondslag ligt – mogelijk is het een ongewoon kwalijk mengsel van deze karaktereigenschappen, maar ik kan me voorstellen dat in sommige gevallen, indien de criticus overduidelijk blijk gaf niet het flauwste benul van het onderwerp te hebben, jullie botte gedrag daar misschien een reactie op was.

¹) Onder een "relativist" moet hier een aanhanger van de natuurkundige relativiteitstheorie, niet van het filosofisch relativisme, worden verstaan.

Laat ik verder niet ingaan op jullie karaktereigenschappen, want dit wil ik je zeggen: vandaag heb ik je persoonlijk opgezocht om te voorkomen dat je je er weer zo gemakkelijk vanaf maakt zoals andere keren. Neem maar van mij aan dat ik niet wegga voor al mijn vragen zijn beantwoord. Je komt er niet onderuit. Ik zal je echter niet teveel onder druk zetten zodat je toch met enige welwilligheid mijn vragen zal beantwoorden. Sterker, ik zal je zelfs een beetje tegemoet komen. Dat ik lid ben van de kring van critici is voor mij namelijk nog geen reden - zoals voor veel van mijn vakbroeders - mij als een hooghartig wezen te gedragen vol eigendunk en een vermeend bovenmenselijk inzicht (zoals je dat zo vaak ziet bij een recensent van wetenschappelijke artikelen of , in het bijzonder, een toneelrecensent).

Ik probeer gewoon logisch na te denken, temeer daar ik best weet dat je met kritiek vaak alleen maar een gebrek aan eigen denkbeelden etaleert. Ik wil je ook niet als een soort deurwaarder lastig vallen – zoals pas geleden één collega-criticus deed – met het verwijt van diefstal van geestelijk eigendom of vergelijkbaar oneervol gedrag. Slechts de behoefte bij te dragen aan het ophelderen van enige punten uit de theorie, punten waarover de meningen behoorlijk ver uiteenlopen, hebben mij ertoe gebracht jou hierover eens stevig te ondervragen.

Bovendien wil ik je dringend verzoeken mij toe te staan dat ik de inhoud van dit gesprek publiceer. Dit omdat mijn vriend, de uitgever Berolinensis, niet alleen zorgen heeft vanwege de papierschaarste*) , maar ook nog uit zijn slaap wordt gehouden door een gebrek aan kopij voor zijn tijdschrift.
*) vertaler: het was vlak na de 1ste wereldoorlog

Ik hoor je niet tegenpruttelen, dus kom ik direct ter zake. Eén van de resultaten uit de speciale relativiteitstheorie is de vertragende invloed van de snelheid op de voortgang van de tijd. Sindsdien worden er voortdurend voorbeelden aangedragen die de theorie weerleggen en – naar mijn mening – op goede gronden. Want met het genoemde resultaat kan men een onvermijdelijk tegenstrijdigheid met de grondbeginselen van de theorie zelf afleiden. Voor de goede orde zal ik dat resultaat nog eens duidelijk omschrijven.

----------------------------------------------------------------------------------------------------------------------------------

Laat K een galileïsch coördinatensysteem zijn zoals bedoeld in de speciale relativiteitstheorie, dat wil zeggen een referentiestelsel ten opzichte waarvan een aan zichzelf overgelaten, stoffelijk punt rechtlijnig en eenparig beweegt. Laat verder U¹ en U² twee precies dezelfde klokken zijn die van buitenaf niet kunnen worden beïnvloed. Deze lopen even snel als ze vlak naast elkaar of op een willekeurige afstand van elkaar staan opgesteld in rust ten opzichte van het stelsel K. Als echter één van de klokken, bijvoorbeeld U² , ten opzichte van K in een toestand van een eenparige, rechtlijnige beweging wordt gebracht, dan zal deze klok volgens de speciale relativiteitstheorie – beoordeeld vanuit het coördinatenstelsel K – langzamer lopen dan de klok U¹, die ten opzichte van het stelsel K in rust blijft. Deze uitkomst is toch zacht gezegd eigenaardig te noemen.
Er rijzen echter ernstige bezwaren tegen de theorie als men zich het volgende, welbekende gedachte–experiment voor de geest haalt.

Neem twee punten A en B op enige afstand van elkaar in het stelsel K. We spreken af dat A de oorsprong is van het stelsel en dat B op de positieve x–as ligt. Eerst hebben we beide klokken bij het punt A opgesteld. Ze lopen dan even snel en we nemen aan dat hun wijzers dezelfde tijd aanwijzen. We laten nu klok U² met een constante snelheid langs de positieve x–as bewegen tot hij B bereikt. We nemen aan dat de snelheid bij B omkeert zodat de klok U² weer naar A teruggaat. Als de klok bij A komt, wordt hij tegengehouden, zodat hij weer in rust is ten opzichte van klok U¹. Omdat de, vanuit K beoordeelde, eventuele verandering van de wijzerstand van U² gedurende zijn snelheidsverandering bij B beslist niet boven een bepaalde waarde uit kan komen, en omdat U² gedurende de eenparige beweging langs het traject van A naar B en van B naar A langzamer loopt dan U¹, zal, als we de afstand A B voldoende lang nemen, de klok U² na terugkomst altijd achterlopen ten opzichte van U¹.

Ben je het met deze conclusie eens?

De Relativist:
Geheel mee eens. Ik heb het altijd jammer gevonden dat sommige schrijvers die overigens de principes van de relativiteitstheorie onderschrijven, deze onontkoombare gevolgtrekking proberen te omzeilen.

De criticus:
Maar nu komt het probleem. Volgens het relativiteitsprincipe moet de gehele gebeurtenis op precies dezelfde wijze verlopen wanneer deze vanuit het coördinatenstelsel K* wordt waargenomen, dat met de klok U² meebeweegt. Ten opzichte van K* is het dan de klok U¹ die heen– en weer beweegt, terwijl de klok U² voortdurend in rust blijft. Daaruit volgt dan dat aan het eind van de beweging U¹ ten opzichte van U² achter moet lopen, wat in strijd is met het eerder genoemde resultaat. Zelfs de meest trouwe aanhangers van de theorie kunnen toch moeilijk beweren dat twee naast elkaar staande klokken elk ten opzichte van de ander achterloopt.

De relativist:
De laatste bewering is uiteraard niet te weerleggen. Maar het gehele slotbetoog is echter ontoelaatbaar omdat volgens de speciale relativiteitstheorie de twee coördinatenstelsels K en K* beslist geen gelijkwaardige stelsels zijn. De theorie neemt immers slechts de gelijkwaardigheid aan van alle galileïsche (niet versnelde) coördinatenstelsels, dat wil zeggen die coördinatenstelsels ten opzichte waarvan geheel aan zichzelf overgelaten massapunten zich rechtlijnig en eenparig voortbewegen.
Het stelsel K is zo'n coördinatenstelsel, het stelsel K* echter, dat tijdelijk aan een versnelling is blootgesteld, is dat niet. Daarom kan men uitsluitend uit het feit dat de klok U² na zijn heen– en terugreis achterloopt ten opzichte van U¹ geen strijdigheid met de grondbeginselen van de theorie afleiden.

De criticus:
Ik geef toe dat je op die manier dit bezwaar weliswaar ontzenuwt, maar ik moet erbij zeggen dat ik me door jouw argument eerder overbluft voel dan overtuigd. Als men zich bovendien baseert op de uitgangspunten van de algemene relativiteitstheorie blijft mijn bezwaar recht overeind. Aangezien daarin coördinatenstelsels van willekeurige bewegingstoestanden zijn toegestaan, kan de daarnet beschreven loop van de gebeurtenissen evengoed op het stelsel K* dat met de klok U² meebeweegt, betrekking hebben als op het stelsel K.

De relativist:
Het is beslist zo dat we volgens de algemene relativiteitstheorie evengoed van het stelsel K* als van het stelsel K kunnen uitgaan. Men kan echter gemakkelijk inzien dat de stelsels K en K* met betrekking tot het beschouwde bewegingsverloop geenszins gelijkwaardig zijn. Terwijl namelijk het proces vanuit stelsel K gezien op de manier moet worden opgevat zoals boven is omschreven, doet het zich vanuit K* gezien geheel anders voor, zoals hierna wordt aangetoond waar de twee beschouwingen met elkaar worden vergeleken.

Betrokken op het stelsel K

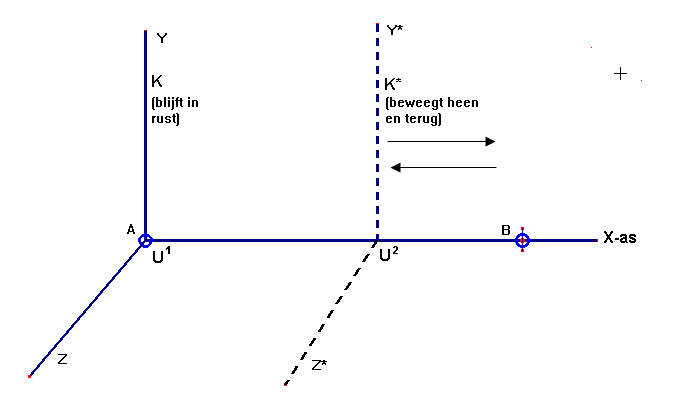
De klok U² wordt in de richting van de positieve X–as door een uitwendige kracht versneld, tot hij de snelheid v heeft gekregen. U¹ blijft in rust.

U² beweegt met een constante snelheid v tot aan het punt B op de positieve x–as. U¹ blijft in rust.

De klok U² wordt door een uitwendige kracht zo lang versneld in de richting van de negatieve x–as tot hij een snelheid v in de richting van de negatieve x–as heeft gekregen. U¹ blijft in rust.

U² beweegt met constante snelheid v in de richting van de negatieve x–as terug tot in de nabijheid van U¹. De klok U¹ blijft in rust.

De klok U² wordt door een uitwendige kracht afgeremd en tot stilstand gebracht.

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Betrokken op het stelsel K*

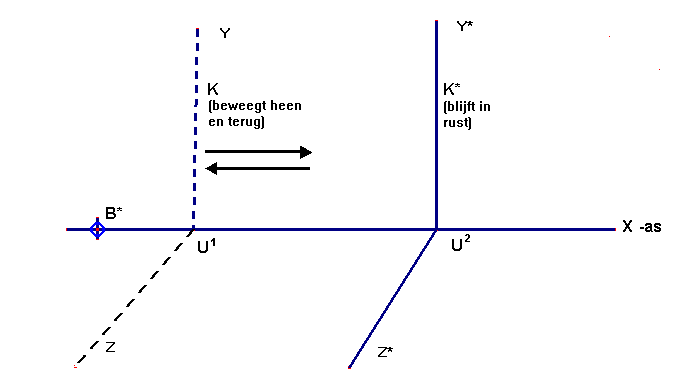
Er ontstaat in de richting van de negatieve x–as een zwaartekrachtveld waarin de klok U¹ zo lang versneld wordt tot hij de snelheid v heeft gekregen. Een uitwendige kracht die op U² aangrijpt, in de richting van de positieve x –as verhindert dat de klok U² door het zwaartekrachtveld in beweging komt. Als de klok U¹ de snelheid v heeft verkregen verdwijnt het zwaartekrachtveld weer.

U¹ beweegt met constante snelheid tot aan het punt B* op de negatieve x–as. U² blijft in rust.

Er ontstaat een homogeen zwaartekrachtveld in de richting van de positieve x–as, onder welks invloed de klok U¹ zo lang in de richting van de positieve x–as wordt versneld tot de klok in die richting een snelheid v heeft verkregen. Hierop verdwijnt het zwaartekrachtveld weer. Een op de klok U² aangrijpende uitwendige kracht in de richting van de negatieve x–as voorkomt dat U² door het genoemde zwaartekrachtveld in beweging geraakt.

Klok U¹ beweegt met constante snelheid v in de richting van de positieve x–as tot in de nabijheid van U². De klok U² blijft in rust.

Er ontstaat een zwaartekrachtveld in de richting van de negatieve x–as waardoor de klok U¹ tot stilstand komt. U² wordt hierbij door een uitwendige kracht in zijn toestand van rust gehouden.

Men moet zich er goed van bewust zijn dat zowel in het deel "Betrokken op stelsel K" als in het deel "Betrokken op stelsel K* " precies hetzelfde verloop der gebeurtenissen is beschreven, de eerste beschrijving heeft slechts betrekking op het coördinatenstelsel K en de tweede beschrijving heeft betrekking op het stelsel K*. Volgens beide beschrijvingen loopt de klok U² aan het eind van het beschouwde bewegingsverloop met een bepaalde hoeveelheid tijd achter ten opzichte van klok U¹. Betrokken op het stelsel K* moet dit verschijnsel als volgt worden verklaard: Gedurende de deelprocessen 2.) en 4.) loopt weliswaar de met een snelheid v bewegende klok U¹ langzamer dan de in rust verkerende klok U² , echter, dit achterlopen wordt overgecompenseerd door een sneller lopen van U¹ gedurende het deelproces 3.). Volgens de algemene relativiteitstheorie loopt een klok namelijk des te sneller naarmate de zwaartekrachtpotentiaal op de plek waar hij zich bevindt hoger is en U¹bevindt zich gedurende het deelproces 3.) daadwerkelijk op een plaats met een hogere zwaartekrachtpotentiaal dan U² . Een berekening leert dat dit sneller lopen precies tweemaal zoveel uitmaakt als het langzamer lopen gedurende de deelprocessen 2.) en 4.) .

Volgens deze beschouwing is uw zogenaamde paradox volledig opgehelderd.

----------------------------------------------------------------------------------------------------------------------------

De criticus:
Je weet je er inderdaad heel handig uit te praten, maar ik zou niet de waarheid spreken als ik zei dat je mij volkomen hebt overtuigd. De netelige kwestie is namelijk niet opgelost, maar op een andere plaats weer opgedoken. Jouw beschouwing laat mij namelijk ineens de samenhang zien tussen het daarnet besproken probleem en een andere moeilijkheid die ook vaak wordt genoemd. Je lost de paradox namelijk op door de invloed op de klokken van een ten opzichte van K* heersend zwaartekrachtveld in rekening te brengen. Maar is dit zwaartekrachtveld niet gewoon verzonnen? Het bestaat immers alleen maar als gevolg van de coördinatenkeuze. Werkelijke zwaartekrachtvelden worden altijd door massa’s voortgebracht en kunnen niet door het kiezen van een geschikt coördinatenstelsel tot verdwijnen worden gebracht. Hoe kan je nu denken dat een louter fictief zwaartekrachtveld invloed kan uitoefenen op de loopsnelheid van een klok?

De relativist:
In de eerste plaats moet ik u er op wijzen dat we met het onderscheid realistisch – niet realistisch weinig verder komen. Hoewel het met betrekking tot K niet aanwezig is, "bestaat" het zwaartekrachtveld ten opzichte van K* even goed als iedere andere natuurkundige grootheid die uitsluitend ten opzichte van een coördinatenstelsel kan worden gedefinieerd. Dit is niet heel bijzonder zoals men snel inziet bij het volgende, aan de klassieke mechanica ontleende voorbeeld. Niemand twijfelt aan de "realiteit" van de kinetische energie, aangezien men anders er toe zou kunnen komen de realiteit van "energie" in zijn geheel te verwerpen. Het is echter duidelijk dat de kinetische energie van een voorwerp afhankelijk is van de bewegingstoestand van het coördinatenstelsel; door een juiste keuze van het stelsel kan men het kennelijk zo voor elkaar krijgen dat de kinetische energie van het voortbewegende voorwerp op zeker ogenblik ergens een van te voren vastgestelde positieve waarde of de waarde nul aanneemt. In het speciale geval dat verschillende massa’s een even grote snelheid in dezelfde richting hebben, kan men door een geschikte keuze van het coördinatenstelsel de gezamenlijke kinetische energie gelijk aan nul maken.
Deze analogie lijkt mij compleet te zijn.

    In plaats van "realistisch" en "onrealistisch" zullen we een duidelijker onderscheid moeten maken tussen grootheden die in het natuurkundige stelsel op zichzelf staan (onafhankelijk van het gekozen coördinatenstelsel) en grootheden die van het coördinatenstelsel afhangen. De volgende stap zou zijn de voorwaarde te stellen dat de natuurkunde in haar wetten slechts grootheden van de eerste soort invoert. Het is echter gebleken dat deze weg praktisch niet realiseerbaar is, zoals de ontwikkeling van de klassieke mechanica duidelijk heeft aangetoond. Men zou er bijvoorbeeld aan kunnen denken, en men heeft dat ook daadwerkelijk geprobeerd, in de wetten van de klassieke mechanica in plaats van coördinaten alleen maar de onderlinge afstanden tussen de massapunten in te voeren; naar verwachting konden op die manier de doelstellingen van de relativiteitstheorie het eenvoudigst worden bereikt. De wetenschappelijke ontwikkeling heeft dit vermoeden echter niet bevestigd. Het lukt niet zonder een coördinatenstelsel en we moeten dus in de vorm van de coördinaten grootheden accepteren die niet opgevat kunnen worden als het resultaat van een goed gedefinieerde meting. Volgens de algemene relativiteitstheorie zijn de vier coördinaten van het ruimte–tijd continuüm zelfs geheel willekeurig te kiezen parameters waaraan iedere zelfstandige natuurkundige betekenis ontbreekt. Echter ook de grootheden (de veldcomponenten) waarmee de natuurkundige realiteit wordt beschreven, zijn voor een deel behept met de genoemde willekeur.
Slechts sommige, in het algemeen tamelijk ingewikkelde uitdrukkingen, die uit veldcomponenten en coördinaten zijn opgebouwd, komen overeen met onafhankelijk van het coördinatenstelsel meetbare (dat wil zeggen reële) grootheden. Maar bijvoorbeeld, de component van het zwaartekrachtveld in een ruimte–tijdpunt is nog niet zo'n van de coördinatenkeuze onafhankelijke grootheid; het zwaartekrachtveld op een bepaalde plaats mogen we dus niet omschrijven als "fysisch reëel" ; wel echter dit zwaartekrachtveld in relatie tot andere gegevens. Men kan dus niet zeggen dat het zwaartekrachtveld op zekere plaats iets "reëels" is, noch dat het alleen maar "zuiver fictief" is.

    De samenhang tussen de in de vergelijkingen optredende grootheden en de meetbare grootheden in de algemene relativiteitstheorie is veel minder direct dan waar men aan gewend is. Dat is de voornaamste moeilijkheid die zich bij het bestuderen van de theorie voordoet. Ook uw laatste bezwaar berust erop dit niet consequent voor ogen te hebben gehouden.

U kenschetste de in het voorbeeld met de klokken opgevoerde zwaartekrachtvelden ook nog als louter fictief omdat de krachtlijnen van "reële" zwaartekrachtvelden noodzakelijkerwijs door massa's zouden moeten worden opgewekt, terwijl in het behandelde voorbeeld er geen massa's aanwezig zijn die deze velden zouden kunnen opwekken. Hier kunnen we op twee manieren op ingaan.
Ten eerste is het geen uitgemaakte zaak dat de opvatting, behorend bij de theorie van Newton, dat ieder zwaartekrachtveld door een massa moet worden opgewekt, ook in de algemene relativiteitstheorie geldt. Deze vraag hangt ook weer samen met wat we daarnet hebben gezien, namelijk dat de betekenis van de veldcomponenten veel minder direct is gedefinieerd dan in de theorie van Newton.
Ten tweede kan men niet beweren dat er geen massa's aanwezig zijn waarmee de opgewekte velden zouden kunnen samenhangen.

Overigens mogen de in versnelling verkerende coördinatenstelsels uiteraard niet als de reële oorzaak van het veld worden gezien. Deze mening meende een criticus met enig gevoel voor humor mij eens te moeten toeschrijven.

We kunnen namelijk alle sterren, die in het heelal aanwezig zijn, zien als deelnemers in het opwekken van het zwaartekrachtveld, want zij zijn gedurende de versnellingsfase van het coördinatenstelsel K* ten opzichte van dit stelsel in versnelling en kunnen op die manier een zwaartekrachtveld induceren, zoals een versneld bewegende elektrische lading een elektrisch veld induceert. Een benaderende wiskundige berekening, uitgaande van de zwaartekrachtvergelijkingen, laat zien dat een dergelijke inductiewerking van een versneld bewegende massa daadwerkelijk moet optreden. Vanuit deze gedachtegang is het duidelijk dat een volledige verklaring van het door u opgeworpen probleem slechts kan worden bereikt als men zich in overeenstemming met de theorie een voorstelling kan maken van de geometrisch–mechanische toestand van het gehele heelal. Dat heb ik het afgelopen jaar geprobeerd en ik ben tot een – volgens mij –volledig sluitende opvatting gekomen; maar om hierop in te gaan, zou nu te ver voeren.

De criticus:
Na deze laatste uiteenzetting krijg ik inderdaad de indruk dat uit de klokkenparadox geen innerlijke tegenspraak van de relativiteitstheorie kan worden afgeleid. Het zou zelfs zo kunnen zijn dat de theorie überhaupt niet behept is met innerlijke tegenstrijdigheden, maar daaruit hoeft niet te volgen dat men de theorie serieus zou moet nemen. Ik zie werkelijk niet in waarom men zich van die complexe en walgelijke rekentechnische moeilijkheden op de hals zou moeten halen vanwege een gedachtespeeltje –het idee van relativiteit – . Dat deze moeilijkheden buitensporig zijn, is uit jouw laatste antwoord duidelijk genoeg gebleken. Daarom zal toch nooit iemand het in zijn hoofd halen om de bewegingen van de hemellichamen van ons zonnestelsel, zoals volgens de relativiteitstheorie kan, op een geocentrisch coördinatenstelsel te betrekken dat bovendien aan de draaibeweging van de aarde deelneemt! Men kan dit coördinatenstelsel, dit "stelsel–in–rust", toch niet als evenwaardig beschouwen, terwijl de vaste sterren met ongekende snelheden rond de aarde suizen? Zo'n aanpak gaat in tegen het gezonde verstand en tegen de wens rationeel te denken.

Het is goed om hier de scherpe uitspraken te herhalen die de heer Lenard kortgeleden over dit onderwerp heeft gedaan. Nadat hij de speciale relativiteit had besproken, waarbij het "bewegende" coördinatenstelsel wordt voorgesteld als een rijdende trein, zei hij: "Men laat nu plotseling de fictieve trein een grote snelheidsverandering ondergaan. Als hierbij door de traagheidswerking in de trein een puinhoop ontstaat, terwijl daarbuiten alles onbeschadigd blijft, dan zal naar mijn mening alleen een zieke geest tot een andere slotsom komen dan dat het gewoon de trein was waarvan de beweging met een schok was veranderd en niet de omgeving. Volgens de simpele betekenis van het veralgemeniseerde relativiteitsprincipe moet in dit geval de mogelijkheid open worden gelaten dat het toch de omgeving is geweest die de snelheidservaring had ondervonden en dat het gehele ongeluk in de trein slechts een gevolg is van een plotselinge ruk die de buitenwereld maakte, waardoor een "zwaartekrachtwerking" van de buitenwereld op het inwendige van de trein ontstond. Op de voor de handliggende vraag waarom de kerktoren naast de trein niet instort als hij tezamen met zijn omgeving die plotselinge schok ondervindt en waarom de gevolgen van de schok zo eenzijdig alleen maar in de trein zijn terug te vinden, terwijl nochtans geen eenduidige uitspraak over de plaats van de bewegingsverandering kan worden gedaan – heeft het principe kennelijk geen antwoord dat een gewoon mens kan volgen ."

De relativist:
Om meer dan één reden moeten wij de complicaties die de theorie ons brengt, welwillend onder ogen zien. In de eerste plaats stelt het een logisch denkend mens innig tevreden om te zien dat het begrip absolute beweging, dat in de kinematica geen betekenis heeft, niet behoeft te worden ingevoerd in de natuurkunde. Het kan niet worden ontkend dat het fundament van de natuurkunde door het vermijden van dit begrip aan logische opbouw heeft gewonnen. Verder eist het feit dat de zware massa en de trage massa van een voorwerp aan elkaar gelijk zijn dringend om een verklaring. Afgezien hiervan heeft de natuurkunde een methode nodig om een veldtheorie voor de zwaartekracht te kunnen opstellen. Zonder een doeltreffend beperkend principe zouden de theoretici zich nauwelijks aan dit probleem kunnen wagen omdat er zeer veel theorieën kunnen worden opgesteld waaraan de beperkte hoeveelheid fysische verschijnselen rond de zwaartekracht zouden kunnen voldoen. Dit luxeprobleem is naast vele andere, een venijnige tegenstander die er op uit is het leven van de theoreticus te vergallen. Dankzij het postulaat van de relativiteit worden de mogelijkheden dermate beperkt dat het pad kon worden uitgestippeld waarlangs de theorie zich zou moeten ontwikkelen. Met de verklaring van de seculaire perihelium beweging van de planeet Mercurius werd de kroon op het werk gezet. Het bestaan van dit afwijkende gedrag was door de sterrenkundigen overtuigend aangetoond, maar de verklaring ervan wilde op basis van de theorie van Newton niet naar tevredenheid lukken.

– Met de bewering van de principiële gelijkwaardigheid der coördinatenstelsels wordt niet bedoeld dat ieder coördinatenstelsel voor het onderzoek van een bepaald natuurkundig systeem in dezelfde mate geschikt is; dit verschilt niet van de klassieke mechanica. Streng genomen mag men bijvoorbeeld niet zeggen dat de aarde zich in een ellips om de zon beweegt, daar deze uitspraak immers al een coördinatenstelsel impliceert waarin de zon in rust is, terwijl de klassieke mechanica toch ook stelsels toelaat ten opzichte waarvan de zon rechtlijnig en eenparig beweegt. Zo min het echter bij iemand opkomt zich van zo'n stelsel te bedienen bij het onderzoek van de aardbeweging, zo min zal hij bij zijn beschouwing van de aardbeweging tot de slotsom komen dat het coördinatenstelsel, waarvan de oorsprong zich voortdurend in het zwaartepunt van het beschouwde mechanische systeem bevindt, een principieel bevoorrechte positie ten opzichte van ieder ander coördinatenstelsel heeft.
Zo is het ook bij het door u genoemde voorbeeld.
Niemand zal bij het onderzoek van het zonnestelsel gebruik maken van een coördinatenstelsel dat in rust is ten opzichte van de aarde omdat dit onpraktisch zou zijn. In principe echter is zo'n coördinatenstelsel volgens de algemene relativiteitstheorie volstrekt gelijkberechtigd ten opzichte van elk ander. De omstandigheid dat de vaste sterren met ongekende snelheden rondlopen als men een dergelijk coördinatenstelsel als basis kiest voor een beschouwing, vormt geen argument tegen de toelaatbaarheid, maar slechts tegen de doelmatigheid van de keuze van dit coördinatenstelsel. Hetzelfde geldt voor het op dit coördinatenstelsel betrokken zwaartekrachtveld: dit krijgt een complexe structuur waarin bijvoorbeeld de componenten die de centrifugale krachten weergeven een plaats moeten krijgen.
Op dezelfde wijze moeten we ook het voorbeeld met de trein van de heer Lenard bezien. Men mag op basis van de relativiteitstheorie deze gebeurtenis niet opvatten als: "dat het misschien toch de omgeving (van de trein) is geweest, die de verandering van de snelheid heeft ervaren". Het gaat niet om twee verschillende , elkaar uitsluitende hypothesen over waar de beweging is gezeteld, maar veel eer om twee principieel gelijkwaardige manieren om dezelfde toedracht te beschrijven^1. .

Dat de kerktoren niet instort, komt, ingevolge de tweede beschrijvingswijze, doordat deze tezamen met de bodem en de gehele aarde in een ( gedurende de schok aanwezig) zwaartekrachtveld in vrije val verkeerd, terwijl de trein door uitwendige krachten (remkrachten) wordt verhinderd om aan de vrije val deel te nemen. Een vrij vallend voorwerp gedraagt zich in dit verband als een vrij zwevend voorwerp, dat gevrijwaard is van alle uitwendige invloeden.

Welke beschrijving men zou moeten kiezen, kan uitsluitend worden beslist op doelmatigheidsgronden en niet op argumenten van principiële aard. Om in deze kwesties het zogenaamde "gezonde verstand" als scheidsrechter aan te roepen, is niet de aangewezen weg zoals het volgende tegenvoorbeeld laat zien.
Lenard zelf zegt dat er tegen de geldigheid van de speciale relativiteitstheorie (d.w.z het relativiteitsprincipe met betrekking tot eenparige translatiebewegingen van de coördinatenstelsels) tot op heden geen goede bezwaren zijn ingebracht. De eenparig rijdende trein kan even goed als "in rust" worden gezien als de rails tezamen met de totale omgeving als "in rust" kan worden gezien. Zou dat voor het "gezonde verstand" van de bestuurder van de locomotief acceptabel zijn? Hij zal er tegen inbrengen dat hij toch niet de omgeving onafgebroken moet verhitten en smeren, maar toch de locomotief, en dat in overeenstemming daarmee zijn arbeid tot uitdrukking komt in de beweging van de laatste.

De criticus:
Na dit gesprek moet ik toegeven dat het minder gemakkelijk is dan ik dacht om jullie opvattingen te weerleggen. Ik blijf weliswaar nog met vele bezwaren zitten, maar ik wil je daar nu niet mee lastigvallen omdat ik eerst ons huidige gesprek eens rustig wil overdenken. Voor ik je weer alleen laat, wil ik je nog één vraag stellen. Het gaat niet om een bezwaar tegen de relativiteitstheorie, maar het betreft een vraag die ik louter uit nieuwsgierigheid stel:
"Hoe staat het er nu voor met de zieke man van de theoretische natuurkunde, de ether, die velen van jullie al morsdood hebben verklaard?"

De relativist:
De zieke man heeft weliswaar een bewogen geschiedenis achter de rug, maar men kan beslist niet zeggen dat hij nu dood is. Vóór de tijd van Lorentz bestond hij uit een in alles dringende gasachtige vloeistof, die bovendien van auteur tot auteur andere eigenschappen meekreeg. Met de theorie van Lorentz werd de ether star en werd gesymboliseerd door het "in rust" verkerende coördinatenstelsel dat daarmee een bevoorrechte bewegingstoestand in het heelal werd. Met de komst van de speciale relativiteitstheorie werd een bevoorrechte bewegingstoestand uitgesloten. Dit kwam neer op een verloochenen van de ether in de zin van de vroegere theorieën want zou er een ether bestaan, dan zou hij in ieder punt van de ruimte–tijd een zekere snelheid hebben, die effecten in de optica teweeg zou moeten brengen. Zoals gezegd, een dergelijke bevoorrechte bewegingstoestand bestaat niet, zoals de speciale relativiteitstheorie leert, en daarom bestaat er ook geen ether in de oude betekenis. De algemene relativiteitstheorie kent evenmin een bevoorrechte bewegingstoestand in een punt van de ruimte die men als zoiets als de snelheid van de ether zou kunnen interpreteren. Terwijl echter volgens de speciale relativiteitstheorie een stukje ruimte zonder materie of een elektromagnetisch veld eenvoudigweg leeg, d.w.z door geen natuurkundige grootheden gekarakteriseerd, is te noemen, heeft volgens de algemene relativiteitstheorie de in deze zin lege ruimte toch natuurkundige eigenschappen. Deze worden door de componenten van de zwaartekrachtpotentiaal wiskundig beschreven en leggen de meetkundige verhoudingen van dit ruimtedeel en het daar aanwezige zwaartekrachtveld vast. Men kan deze natuurkundige toestand heel goed zo opvatten dat men van een ether mag spreken, waarvan de eigenschappen van punt tot punt voortdurend variëren. Men moet zich er alleen voor hoeden aan deze "ether" stoffelijke eigenschappen (bijvoorbeeld op elke plaats een bepaalde snelheid) toe te kennen.

                                                    –––––––––––––

Terug