Naar
Uitleg Klokken
Naar Entree
Een geluidanalogon voor de speciale
relativiteitstheorie
Henk Dorrestijn
Juli
2011
Einstein stelde zich (vrij vertaald) de vraag: “Hoe kan
je de lengte meten van een passerende trein die een snelheid v heeft?”.
Dat kan op twee manieren:
-
Je zorgt er op de een of andere manier voor dat je je op de
rijdende trein bevindt en met een duimstok meet je zijn lengte
-
Vanaf het perron, maar dat is een stuk lastiger omdat de tijd er
in moet worden betrokken
Ik zal het verhaal vertellen voor een trein waarin zich
twee conducteurs bevinden en een perron waarop zich enige perronchefs ophouden.
Alle personen zijn voorzien van een duimstok en hebben eenzelfde goed lopende
klok bij zich.
Ad 1. In
de trein kunnen de conducteurs de lengte gewoon opmeten met een duimstok. De
lengte ℓ die ze vinden, is – volgens het
klassieke Relativiteitsprincipe - dezelfde lengte die ook wordt gevonden als de
trein zou stilstaan langs het perron en de perronchefs met een duimstok de
lengte zouden opmeten. Want ten opzichte van de conducteurs is de rijdende trein
een stilstaand object.
Ad 2. Vanaf
het perron moet de bewegende trein op andere wijze worden gemeten en daarbij heb
je goed lopende klokken nodig.
 | Einstein
stelde voor om de lengte van de bewegende trein te bepalen met behulp van
twee klokken op het perron: je kan op één tijdstip met exact gelijklopende
klokken bepalen waar de voor- en de achterzijde van de trein zich bevinden.
Hij voegde er raadselachtig aan toe dat de door de perronchefs gemeten
lengte r
zal afwijken van de lengte ℓ
die door de conducteurs wordt gemeten. |
 | Of
je bepaalt eerst de snelheid v
van de trein door de tijd op te meten die de punt van de trein over een
zekere afstand doet en je laat de twee tijdstippen vaststellen waarop de
voor- en achterzijde van de trein een bepaalde klok op het perron passeren.
Daaruit is met de snelheid v
de lengte r berekenen. |
Overigens zou je kunnen denken dat de lengte van de trein
ook zou kunnen worden opgemeten met behulp van een wieltje dat tegen de zijkant
van de passerende trein wordt gedrukt, maar daarbij lopen we tegen het probleem
aan dat we de lengte niet kennen van de omtrek van dit bewegende wieltje. Dat
was immers het probleem: wat is de lengte van iets dat beweegt.
De meting van de lengte van de bewegende trein kan op nog
andere manieren plaatsvinden, bijvoorbeeld:
 | Door
de twee conducteurs te vragen -
de één zit achterin de trein en de ander voorin -
om tegelijkertijd vlak naast hun trein een gat in het perron te
schieten (uiteraard na toestemming van het betreffende ministerie). Opdat ze
tegelijkertijd zullen schieten, zullen de conducteurs vooraf moeten
controleren of hun klokken wel exact gelijklopen. Vervolgens meten de
perronchefs met een duimstok de afstand tussen beide gaten. |
In dit geval zullen de perronchefs aanvoeren dat de meting
ongeldig is want volgens hen schoten de conducteurs niet gelijktijdig. Hier zit
het probleem: gelijktijdig voor de conducteurs is niet hetzelfde als
gelijktijdig voor de perronchefs. Daar gaan we in het hierna volgende uitgebreid
op in.
 | Het
is een probleem om twee klokken gelijk te laten lopen die zich ten opzichte
van een waarnemer verplaatsen. Voor klokken die zich t.o.v. elkaar of de
waarnemer niet verplaatsen, gaf Einstein een handig meetrecept, de klokkentest,
waarbij geldt: als een lichtsignaal door de lege ruimte tussen twee klokken even
lang over de heenweg doet als over de terugweg lopen ze gelijk. |
Iedere geïnteresseerde lezer weet dat de uitkomst van al
deze metingen is dat de klokken in de passerende trein trager lopen
(tijddilatatie) dan op het perron en dat de lengte van de trein vanaf het perron
gemeten een stukje kleiner is (Lorentzcontractie). Het is echter voor een gewoon
mens heel moeilijk om zich daar een voorstelling van te maken en daarom heb ik
gezocht naar een mogelijkheid iets hiervan te demonstreren. Daartoe heb ik
nagegaan hoe alles zou uitpakken als je geluid als communicatiemiddel zou
gebruiken in plaats van licht. Waarschijnlijk is dat al vele keren eerder
gedaan, maar daar wil ik mij vooralsnog – als niet-wetenschapper - niet in
verdiepen.
Ik wil de relativiteitstheorie “aanschouwelijk” maken
via een analogon met geluid. Dat kan door ons voorstellen dat we allemaal
geblinddoekt zouden worden en dat alle communicatie via GELUID zou verlopen. We
zijn dan GELUIDMENSEN geworden.
Hoe moet je dan met de grootheden lengte en tijd omgaan?
Een lengte kan je ook als GELUIDMENS gewoon opmeten met een duimstok, maar de
tijd kan je niet op enige afstand gewoon
aflezen van een ECHTE KLOK. Je zou echter een GELUIDKLOK kunnen maken die via
geluid de tijd aangeeft. Laten we bijvoorbeeld een geluidklok maken van –
pakweg - 34 cm lengte (eenduizendste
van de geluidsnelheid) waarin een (ultrasoon) geluidsignaal tussen de voor- en
achterzijde heen en weer wordt gezonden via een kleine zender en ontvanger. Na
duizend weerkaatsingen is er een seconde verlopen. Je kunt daarmee in principe
zeer nauwkeurig de tijd weergeven. Via een luidspreker hoort men iedere seconde
een tik en een stem meldt hoeveel minuten en uren er zijn verlopen. Het zijn
open klokken waar de lucht vrijelijk doorheen kan stromen.
We gaan er van uit dat het op het perron en in de omgeving
windstil is. Twee klokken die op enige afstand van elkaar op het perron staan
opgesteld lopen gelijk (volgens het recept van Einstein) als het geluidsignaal
even lang over de heenweg tussen de klokken doet als over de terugweg. We zorgen
er voor dat alle klokken op het perron gelijklopen.
We helpen vervolgens twee geblinddoekte conducteurs op de
stilstaande trein en ieder van hen krijgt een dergelijke gelijklopende klok mee,
plus een duimstok. Elke minuut horen ze de stem die de tijd vermeld en de
bijbehorende “seconde tikken”.
Wij vragen de conducteurs om hun klok aan de buitenkant van
de trein - zowel voor als achter – te bevestigen. Wat gebeurt er met de
tijdaanwijzing van zo’n klok aan de buitenkant als de trein snelheid krijgt?
Dan stroomt de lucht met een snelheid v door de klok.
De conducteurs zullen zeggen dat de snelheid van het geluid
in de klok op de heenweg – vanwege de tegenwind - kleiner is dan op de
terugweg.
Dat zien de perronchefs anders: het geluid gaat op de
heenweg even snel als op de terugweg, maar de klók verplaatst zich in die
tussentijd door de stilstaande lucht.
Hoe het ook zij, de klok gaat langzamer tikken! Immers, als
het geluid in de klok zich in de richting van de bewegende trein voortplant,
duurt het langer voor het geluid de andere kant van de klok bereikt en als het
geluid de andere kant op beweegt, duurt het minder lang. Het eindresultaat is
altijd dat het geluid er in totaliteit langer over doet om heen en weer
te gaan dan bij een klok die zich niet verplaatst.
 | Voorbeeld:
Een bootje vaart 3 km per uur over stilstaand water. Als het water echter
stroomt met 1 km/uur dan is de
snelheid tegen de stroom in 2 km/uur en met de stroom mee 4 km/uur. Als de
afstand tussen twee punten 6 km is, dan is de afstand heen en terug 12 km.
Zonder stroming doet het bootje daar 4 uur over, maar mét stroming 3 uur
heen en 1,5 uur terug, dus samen 4,5 uur.. Dat duurt langer!! |
Als die trein niet te veel lawaai maakt, horen de
perronchefs dus boven het geluid van de trein uit, dat de klokken langzamer
lopen dan hun eigen klokken. De perronchefs vragen vervolgens aan de conducteurs
om eens te controleren of de klokken onderling wel gelijklopen.
Als de trein opnieuw passeert steekt de achterste
conducteur zijn hoofd door het raam naar buiten en blaast op zijn fluitje. Voor
de conducteurs heeft de trein de lengte
ℓ
maar het geluid moet een grotere afstand dan ℓ
afleggen om de voorste klok te bereiken,; er komt namelijk de afstand
bij die de trein aflegt in de tijd die het geluid erover doet om de voorste klok
te bereiken. Op de terugweg wordt de afstand korter.
 | Overigens
blijkt hieruit dat een snelheid groter dan de geluidsnelheid voor de
GELUIDMENS onmeetbaar is. Vergelijk dit met wat Einstein zei: “Snelheden
groter dan de snelheid van het licht kunnen niet bestaan” |
Hoe lang het geluid er over doet om van klok tot klok heen
en terug te gaan, is gemakkelijk te berekenen door te bedenken dat de relatieve
snelheid van het geluid ten opzichte van de trein op de heenweg wordt verminderd
met de snelheid van de trein en op de terugweg juist verhoogd met die snelheid v.
De geluidsnelheid in stilstaande
lucht noemen we c. De geluidsnelheid wordt dan
c-v op de heenweg en c+v op
de terugweg. De tijdsduur over de heenweg is ℓ/(c
– v) en over de
terugweg ℓ/(c+v)
.
De
geluidklokken lopen dus volgens de conducteurs niet gelijk, want bij gelijklopen
zou de heenweg even lang moeten duren als de terugweg. Zij concluderen dat de
geluidklokken, die gelijkliepen toen ze aan de stilstaande trein werden
bevestigd niet meer gelijk lopen als de trein snelheid krijgt. De voorste klok
moet vóórlopen volgens de conducteurs want als de conducteur aldaar hem
een stukje terugzet, kan hij er voor zorgen dat het geluid volgens de
klokkentest even lang over de heenweg doet als over de terugweg. Dan lopen ze
volgens de conducteurs gelijk.
 | Voorbeeld:
Als de conducteur om één uur op zijn fluitje blaast bij de achterste klok
en het geluid bereikt, afgelezen op de voorste klok, om 0,20 seconden over
één de voorste klok en de weerkaatsing is, afgelezen op de achterste klok,
na 0,30 seconden over één weer terug op het uitgangspunt, dan hoeven de
conducteurs de voorste klok slechts 0,05 seconde terug te zetten om er voor
te zorgen dat de heen- en terugweg volgens hun klokken even lang duurt. |
Hoeveel tijd moeten de conducteurs de voorste klok in
theorie terugzetten opdat zij het idee hebben dat de klokken gelijk lopen?
De tijd over de heenweg tussen de twee klokken min de helft
van de totale tijd heen en terug tussen de twee klokken:
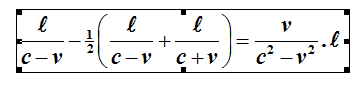
 | Voorbeeld:
Als de trein met een snelheid van 20 m/s beweegt en een lengte heeft van 400
m, dan kunnen we hiermee berekenen – uitgaande van een geluidsnelheid van
340 m/s – dat de voorste klok 0,06944 sec is teruggezet. Het is evenredig
met de lengte en meer dan evenredig met de snelheid van de trein. |
Overigens, als de conducteurs de klokken naar hun idee
gelijk laten lopen door de voorste klok 0,06944 sec terug te zetten , zullen de
perronchefs vinden dat de voorste klok op de trein 0,06944 sec achterloopt op de
andere klok op de trein.
Het eerste probleem dat we tegenkwamen, was dat de klokken
op de trein langzamer liepen dan de klokken op het perron. Hoeveel langzamer
lopen de klokken aan de buitenkant van de trein dan de klokken op het perron?
Dat is een vergelijkbaar probleem.
Het geluid doet er per heen- en teruggang in de klok van 34
cm bij stilstand precies 1 sec over om
500 keer heen en weer te gaan. Bij bovengenoemde snelheid van 20 m/s duurt dat
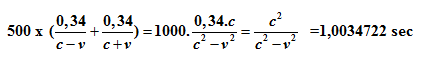
Voor de klok op de trein duurt een seconde 0,0034722 s
langer dan voor een klok die zich niet verplaatst. Na 1 minuut wordt dat
0,208333 sec. Na één uur 12,50 sec.
 | Wanneer
we de twee conducteurs - de één zit achterin de trein en de ander voorin -
vragen om tegelijkertijd (volgens ons) vlak naast hun trein een gat
in het perron te schieten, zodat wij de afstand – de lengte van de trein -
kunnen meten uit de plaatsen
waar het perron is beschadigd, zullen zij protesteren: zo kan je de afstand
niet meten, want we schieten niet tegelijkertijd. De voorste conducteur
schiet 0,06944 sec te snel want zijn klok loopt voor, zegt de achterste.
Daardoor lijkt de trein korter met een afstand van
0,06944 x 20= 1,39 m (Dit is in principe de manier waarop de lengte
van de trein volgens Einstein moet worden gemeten). |
De
analogie
Wat is nu de relatie met de speciale relativiteitstheorie .
Einstein had het uiteraard niet over GELUID dat zich voortplant door de lucht,
maar over LICHT dat zich voortplant door de lege ruimte. Het verhaal is tot op
zekere hoogte vergelijkbaar, want ook de voortplanting van licht zal meer tijd
vragen, gezien vanaf het perron, wanneer het van de achterkant van een rijdende
trein naar de voorkant beweegt dan voor de terugweg. Dus voor iemand op het
perron zullen de ECHTE KLOKKEN op de rijdende trein niet gelijk kunnen lopen als
deze klokken, gemeten via een luchtledige buis, volgens de conducteurs in de
trein wel gelijklopen. Het niet-gelijklopen van de klokken hangt in de speciale
relativiteitstheorie samen met het trager lopen van de klokken en de
Lorentzcontractie.
In dit geluidanalogon zie je eveneens een trager lopen van
de bewegende klokken en ook een soort Lorentzcontractie, maar de effecten zijn
veel en veel groter, maar niet symmetrisch.
Het verschil tussen het geluidanalogon en de speciale
relativiteitstheorie is dat de verschijnselen bij het analogon aan de
eigenschappen van lucht kunnen worden toegeschreven of aan de beweging van de
trein, terwijl voor echte klokken in de lege ruimte de verschijnselen
uitsluitend aan de beweging kunnen worden toegeschreven. Dan komt ook de
symmetrie in het langzamer lopen van de klokken volledig tot zijn recht. De
perronchefs zien de klokken van de conducteurs langzamer lopen terwijl de
conducteurs de klokken op het perron langzamer zien lopen.
Demonstratie
doeleinden
Met GELUIDKLOKKEN kan je aanschouwelijk maken dat de
klokken op een rijdende trein langzamer gaan lopen en dat er een tijdsverschil
ontstaat tussen de voorste klok op een trein en de achterste klok. De oorzaak
kan worden toegeschreven aan de snelheid waarmee de klok door het medium beweegt
waar het signaal zich door voortplant. Geheel in overeenstemming met een klok
die zich door de lege ruimte beweegt als het signaal uit licht bestaat. Maar de
effecten met geluid blijven bestaan als de “trein” stilstaat en er een
luchtstroom langs wordt gevoerd met een snelheid v
. Daarom kunnen demonstraties worden gerealiseerd met klokken die in een
luchtstroom worden geplaatst. Daarmee kan men de effecten op de tijd laten horen
en het publiek een stukje mee laten genieten van de magie van de speciale
relativiteitstheorie.
Terug naar Begin
|
