|
§ 2plus Te vlug geschoten!
Naar Uitleg §3 Wiskunde
Naar Uitleg §2
Naar Uitleg
Inhoud
Naar Portier
Einstein beweert op p. 896 dat de lengte van de bewegende balk
verschilt van de lengte van een rustende balk. Hij toont het echter niet aan!
Hij laat alleen maar zien dat er met die klokken iets geks aan de hand is, ook
interessant, maar het ging om de lengte van de balk. Hij is er zelf over
begonnen en nu willen we het weten ook! Hoe zit het met de lengte van die balk…..!?
Geen antwoord.
 |
We zullen hier een uitleg geven die recht
doet aan de gedachtegang van Einstein. In het boek Op het Spoor
van de Tijd (zie Boek)
laten we zien dat het uitgangspunt van Einstein dat de bewegende
balk en ook de bewegende meetlat zijn gekrompen, onjuist is. Valt
een beetje tegen van Albert. Gelukkig zijn de formules wel juist,
het rammelt echter in de interpretatie. |
We zullen het wel zelf uitzoeken, daar hebben we Einstein niet bij nodig.
"De lengte van de balk terwijl deze voorbijvliegt?" Doen we even.
Het gaat om een idioot probleem: als wij ervoor zorgen dat de klokken van de
cowboys gelijklopen met onze klokken, kunnen de cowboys door een meting laten
zien dat we er naast zitten. De voorste klok bij B loopt
vóór op de
achterste klok bij A. De klokken op de voorbijvliegende balk kunnen niet
gelijklopen volgens de meting.
 | Alleen de cowboys op de balk kunnen volgens het recept van Einstein
bepalen of
de twee klokken gelijklopen, want de klokkentest gold in een
stilstaand stelsel. |
De cowboys op de balk zitten opgescheept met onze tijd, daar zit het probleem.
Als de cowboys echter hún twee klokken gelijkzetten volgens hun inzicht, zien
wij door gelijktijdig de klokken A en B af te lezen dat de voorste
klok B áchterloopt ten opzichte van klok A.
"Het is ook nooit goed!"
Omgekeerd geldt volgens de cowboys voor de klokken die we langs de snelweg
hadden opgesteld (zie fig. 2.01 van §2) dat de voorste klokken
achterlopen op de klokken achteraan. Hierbij is een "voorste klok"
een klok die eerder wordt gepasseerd dan een volgende klok. Het gaat niet om de
afstand tot de klok, want van de gepasseerde klokken is de klok die het eerst
werd gepasseerd en die de cowboys misschien al ver achter zich hebben gelaten, nog steeds de "voorste klok"!
Hoe je het ook wendt of keert, de tijd van de cowboys krijgt andere waarden
dan onze tijd.
Er is nog iets wat goed moet worden afgesproken,
namelijk, wat verstaan we onder de lengte r van een bewegende balk.
Daaronder moeten we de lengte verstaan zoals we die kunnen meten terwijl de balk
beweegt. Dat kan op twee manieren.
1ste We staan zelf stil en we meten de lengte van de
voorbijvliegende balk door op één tijdstip te bepalen waar het beginpunt B en de achterkant
A van de balk zich bevinden
2de We meten op een bepaalde plaats het tijdverschil tussen de
momenten dat de punten B en A op die plaats voorbijkomen en dit
tijdverschil vermenigvuldigen we met de snelheid v van de balk.
De lengte, die de cowboys op de bewegende balk zelf meten, de afstand tussen A
en B, is niet de lengte die we willen weten. Wat zij meten
is namelijk de lengte van de balk–in–rust, omdat de balk waar zij opzitten
voor de cowboys in rust is. Zij meten de lengte met een meetlint dat ze langs de
balk leggen. Die lengte kennen we wel, die is ℓ. Die waarde meten
we zelf ook als we de balk in rust opmeten.
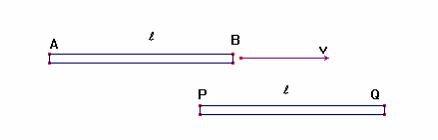
Figuur 2.21 Twee identieke balken
We zullen nu op eigen houtje de lengte r van de balk-in-beweging
bepalen. We gaan uit van twee identieke balken, die beide een lengte ℓ
hebben als je ze in rust meet met een meetlint. De balk waar de cowboys A
en B zich op bevinden, krijgt een snelheid v en vliegt voorbij.
Als je nu zijn lengte meet door de cowboys gelijktijdig (volgens onze
klokken zoals we in §2plus hebben gedaan)
een gat in het wegdek te laten schieten, of door de tijd te meten tussen het
voorbijvliegen van B langs P en van A langs P, dan
meet je de lengte r. In het laatste geval ga je ervan uit dat je de tijd
mag vermenigvuldigen met de snelheid v.
Dit brengt ons op de vraag of de snelheid v van AB ten opzichte
van PQ even groot is als de snelheid van PQ ten opzichte van AB.
Dit lijkt een absurde vraag. We gaan daar altijd van uit. Het is
vanzelfsprekend, maar kunnen we het ook beredeneren? Het antwoord is naar
verwachting: ja.
Als we uitgaan van identieke balken. Identieke balken zijn balken die we op geen
enkele manier van elkaar kunnen onderscheiden als we ze door elkaar gehusseld
hebben. Je weet echt niet welke welke is. Wanneer twee van dergelijke balken
door de lege ruimte bewegen, moeten ze verwisselbaar zijn: wanneer je op PQ zit te kijken naar AB
moet je hetzelfde zien als wanneer je op AB zit te kijken naar PQ,
namelijk een balk ter lengte r die met zekere snelheid beweegt,
want als je op PQ zittend de balk AB met een grotere
snelheid voorbij ziet vliegen dan je op AB zittend de balk PQ
voorbij ziet vliegen, dan is er een onderscheid ontstaan: een snelle balk AB
en een langzame balk PQ. De balken zijn niet meer identiek! Dat is in
strijd met ons uitgangspunt.
Wanneer dit in de lege ruimte geldt, geldt het ook in een ruimte die gevuld is
met lucht of water, want bij snelheidsmetingen speelt het tussenliggende medium
geen rol.
Van het resultaat maken we gebruik. In stappen gaan we naar de conclusie:
Stap 1: Meet de snelheid v van de balk op twee manieren.
Wanneer je de snelheid v van de balk AB wilt meten, dan meet je
de afstand waarover de balk zich heeft verplaatst en je deelt dat door de tijd
die de balk daarvoor nodig had. We beschouwen daartoe het punt B (zie
fig. 2.21) en we meten de tijd die B er over doet om van P
naar Q te geraken. Vervolgens delen we de afstand van P naar Q
door de tijd en we verkrijgen de snelheid. Dat kan op twee manieren: we kunnen
dat zelf doen, vanaf de balk PQ met onze klokken, of we laten het cowboy B
doen vanaf de balk met zijn klok (het symbool voor de tijd die met een klok op
de bewegende balk wordt gemeten, is τ,
de Griekse letter tau).
We krijgen twee uitdrukkingen:
 | Voor ons is de afstand gewoon de lengte ℓ
van een balk in rust
en de tijdsduur met onze klokken is tQ – tP .
Dan is
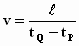 ,
, |
 | De cowboy ziet de afstand van P naar Q als de lengte van
een bewegende balk, dus r. Hij meet een tijdsduur τQ
– τP . Dan
is
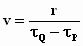 |
Let op: Ogenschijnlijk zijn er meer methoden om de snelheid te meten, maar
voor je het weet, herhaal je de methode, maar dan vanuit het andere stelsel,
waarbij je het stelsel AB tot stilstaand stelsel hebt gebombardeerd! Dat kan in
grote chaos eindigen.
Omdat de snelheid voor beide stelsels v is, mogen we de uitdrukkingen
gelijkstellen:
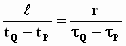 dus
dus 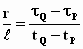
Uit de eerste vergelijking zie je dat de verhouding tussen lengte en
tijdsduur constant is. Als je een gekrompen lengte meet voor de bewegende balk,
vind je ook een kortere tijdsduur voor de passage van de balk. Voor de
tijdsduur tQ – tP en τQ
– τP schrijven
we nu t en τ waarmee de
laatste uitdrukking wordt:
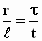 of,
of,
wat op hetzelfde neerkomt: 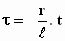 of
of 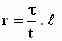
Stap 2: Meet de tijdsduur van het retourtje tussen A en B van het
lichtsignaal op twee manieren.
Over de verhouding 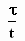 kunnen we een
zeer duidelijke uitspraak doen als we de tijdsduur van de lichtsignaal tussen A
en B volgens de cowboys en volgens ons vergelijken: kunnen we een
zeer duidelijke uitspraak doen als we de tijdsduur van de lichtsignaal tussen A
en B volgens de cowboys en volgens ons vergelijken:
De tijdsduur volgens de cowboys staat in verhouding tot die volgens ons als:
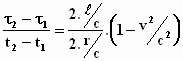
|
|
Verder strepen we de gelijke constanten in de uitdrukking tegen elkaar weg en
we schrijven voor de tijdsduur, het tijdverschil τ2
– τ1 en t2
– t1 weer gewoon de tijd τ
of t. Zo verkrijgen we:
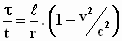
Stap 3: Vergelijk de resultaten van stap 1 en stap 2.
We hebben nu twee uitdrukkingen voor de verhouding τ
/ t en deze moeten dus gelijk aan elkaar zijn:
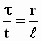 en
en 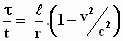
Dan moet gelden: 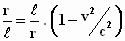 of
of 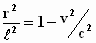
dus 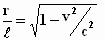
Met de laatste uitdrukking vinden we de door ons gemeten lengte r van
de bewegende balk die volgens de cowboys een lengte ℓ heeft:
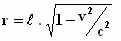 "kortere balk"
"kortere balk"
 | Formules waar we regelmatig op terugkomen, zullen we voor de gezelligheid
een naam geven. |
Omdat 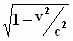 altijd kleiner is dan één,
volgt daaruit dat de bewegende balk korter is dan de balk in rusttoestand
(waarbij je moet bedenken dat de bewegende balk altijd de andere balk is en de
rustende balk is de balk waar je jezelf op of bij bevindt).
altijd kleiner is dan één,
volgt daaruit dat de bewegende balk korter is dan de balk in rusttoestand
(waarbij je moet bedenken dat de bewegende balk altijd de andere balk is en de
rustende balk is de balk waar je jezelf op of bij bevindt).
 | Dit is het resultaat dat Einstein ons onthield, waarschijnlijk om de lijn
van zijn betoog niet te onderbreken. Hij zal wel hebben aangenomen dat
iedereen dit zelf al lang had uitgezocht! |
Stap 4: De tijd nader beschouwd
Voor de tijd op de bewegende balk geldt dus dat hij "langzamer" is
dan onze tijd:
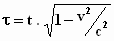 "langzamere tijd"
"langzamere tijd"
Met "langzamer" wordt hier bedoeld dat het leven - alles - op de balk trager
verloopt dan bij ons. Als ze een klok hebben waarvan de slinger volgens hen
iedere seconde heen en weer gaat, dan meten wij dat die slinger er bijvoorbeeld
twee seconde over doet. De klok tikt er trager (volgens ons). Maar ook iemands
haar groeit langzamer en als ze naar ons zwaaien, gaat dat langzamer. Hoe klein de
effecten bij gewone snelheden ook zijn, als we naar een bewegend stelsel kijken,
bekijken we altijd een vertraagde film. "Pratende mensen in een passerende
auto spreken ietsje langzamer dan wanneer de auto voor een stoplicht stilstaat", bij wijze van spreken.
De keerzijde is dat vanuit de auto bezien de mensen op het
trottoir weer langzamer spreken dan de automobilist en zijn passagier.
 | Het is verwarrend. De tijd op de balk verloopt trager en de balk is
ook nog korter geworden en . . . . . het wordt nog erger. |
We leggen vervolgens dat eerder gevonden, uiterst wonderlijke resultaat (zie
§2) ernaast dat de klok B vooraan de balk volgens de cowboys vóórliep op klok
A terwijl wij vanaf de grond zien dat ze gelijklopen. We hadden de
cowboys weliswaar geïnstrueerd de klokken gelijk te laten lopen met onze
klokken en dat hebben ze goed gedaan, maar dat daardoor hun klokken onderling
niet gelijk zouden lopen, dat hadden we niet verwacht. Ze zitten in een ander stelsel, het Stelsel-in-Beweging, en
daarvoor geldt dat het heen en weer gaan van een lichtsignaal tussen de twee
klokken A en B een ander verloop heeft dan bezien vanuit het
Stelsel-in-Rust, waardoor er een tijdsverschil moet zijn
tussen de twee klokken.
Terug
(hoeft niet)
Dat vóórlopen volgt niet direct uit het trager lopen van de klokken. Twee klokken kunnen best trager lopen, maar onderling toch gelijklopen. Om de
juiste tijd op de bewegende balk te vinden, zullen we hier rekening mee moeten
houden.
We zetten op zeker moment, in samenwerking met de cowboys, klok A
gelijk met onze grondklokken. De cowboys laten vervolgens hun klok B
gelijklopen met klok A, door klok B een stukje terug te zetten.
Wij constateren dat klok A en B trager lopen
volgens de formule "langzamere tijd" , dan onze klokken
en dat klok B nog weer een stukje achterloopt op A. Klok B
loopt even snel (of even langzaam) als klok A, maar sukkelt er een stukje
achteraan.
We zullen bepalen hoeveel klok B achterloopt op klok A en we
zullen het resultaat zowel in onze tijd t als met de tijd τ
van de cowboys weergeven.
Uit de meting van de cowboys waarbij ze een gat in het wegdek schoten, bleek
dat de voorste klok vóórliep als de klokken volgens ons gelijkliepen. We
kunnen precies vertellen hoeveel de voorste klok B volgens die meting
vóórloopt op de achterste klok A. Je neemt gewoon het verschil van de
twee tijdmetingen die we vonden voor de tijd die het licht erover doet om van A
naar B te gaan en om van B naar A te gaan (zie §2
Balken ) en we rekenen dat eerst uit:
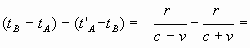
→ Geef beide termen dezelfde noemer (= onder de
deelstreep) namelijk het product (c–v) .(c+v)
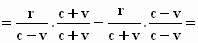
→ Een handigheidje: beide termen zijn eigenlijk met één vermenigvuldigd,
want (c+v)/(c+v) = 1 en (c-v)/(c-v) = 1.
De termen kunnen nu
worden opgeteld omdat ze dezelfde noemer hebben:
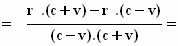
→ Werk de
haakjes in de teller (= boven) weg
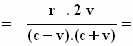
→
Gebruik (c – v) . (c + v) = c2 – v2 = c2.
(1– v2/c2)
en je krijgt:
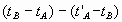 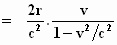
Als klok B één seconde voorloopt op klok A,
dan duurt de heenweg van A naar B volgens de
wijzers van de klok één seconde te lang en de
terugweg duurt één seconde te kort. Het verschil (tB – tA)
– (t'A – tB) is dan twéé seconde. Het
vóórlopen van de klok tikt dubbel door! We moeten de gevonden uitdrukking dus
door twee delen om te weten te komen hoeveel klok B vóórloopt op klok A
als we met de tijd van de grondklokken werken.
Dat levert het tijdverschil Δt op.
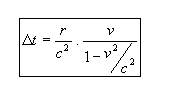
"te vlug geschoten"
Met de gevonden waarde loopt volgens de meting van de cowboys
klok B
vóór op klok A als beide klokken gelijk en even snel lopen als onze
klokken. Als de cowboys klok B, volgens hun inzicht, gelijk
laten lopen met klok A zal volgens óns klok B met de genoemde
tijd Δt àchterlopen op klok A.
Het achterlopen is, zoals je ziet uit de formule "te vlug
geschoten", afhankelijk van de lengte van de balk. Hoe verder B
van A afligt, hoe groter het tijdsverschil. We weten al dat
een klok in het
bewegende stelsel trager tikt. Omdat B op ieder punt in de ruimte langs de x-as kan
worden gekozen, is het van belang om een uitdrukking voor de tijd τB
van het punt B (waarvan de plaats op de x-as in zijn algemeenheid x
wordt genoemd) te vinden, omdat je dan een algemene uitdrukking voor de tijd τ
hebt die overal langs de x–as geldig is.
We laten zien welke tijd voor cowboy B geldt:
De tijd τB van B
loopt dus ten opzichte van de tijd τA
van A een stukje Δτ
achter.
τB = τA
- Δτ
Het stukje Δτ kennen we
in eerste instantie niet, maar we kennen wel het stukje Δt
(volgens onze tijdaanwijzing) dat de klok B achterloopt op klok A.
Maar dan kunnen we Δτ
uitrekenen want we hebben gezien dat tussen de tijd op onze klokken en de tijd
op de klokken van de cowboys de relatie "langzamere tijd"
geldt: 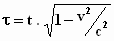
Voor de tijdsduur geldt zo
eveneens:
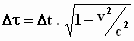 = = 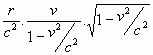 = =
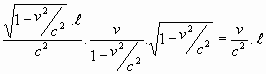
 | Dit is de formule "te vlug geschoten" volgens de cowboys:
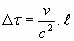 |
Hiermee wordt:
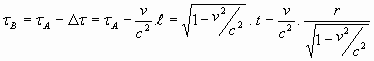
Dit gaan we herschrijven tot we een uitdrukking krijgen die
er wat overzichtelijker uitziet.
De plaats (= de x-waarde) van het punt B ten opzichte van een
beginpunt op de grond, de oorsprong van het stelsel-in-rust, is voor ons op
ieder tijdstip t in de x –richting r groter dan de plaats
van A. (Zie figuur 2.22). Als we afspreken (hetgeen betekent dat
we het op die manier aanpakken, of je het er mee eens bent of niet!) dat A
zich op het tijdstip t = 0 op de plaats x = 0 bevindt, dan
is de plaats van A na enige tijd op het tijdstip t gelijk aan v . t . De
balk vliegt nou eenmaal met de snelheid v langs onze observatieposten.
Omdat wij een lengte r voor de balk meten, is de plaats van B
volgens ons op dat tijdstip
x = v . t + r.
Er geldt dus r = x – v . t
We vullen voor de plaats r in het bewegende stelsel van het punt B
in: r = x – v . t., waarbij x en t waarden zijn die in het
stelsel-in-rust gelden (zie fig. 222). Daarmee krijgen we voor tB
drie termen:
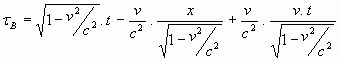
De eerste en de laatste geven we dezelfde noemer en we zetten ze bij elkaar:
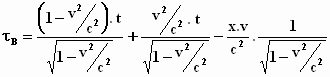
Het is een beetje puzzelen. Nu breng je de eerste en de tweede term aan de
rechterkant onder dezelfde noemer:
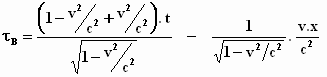
Dit vereenvoudigen we verder tot een overzichtelijke vorm en in plaats van τB
schrijven we gewoon τ , omdat
deze formule algemeen voor de tijd van een punt dat zich op een willekeurige
plaats bevindt in het bewegende stelsel, op de balk dus, voor ieder tijdstip t
in het stelsel-in-rust en voor iedere plaats x in het stelsel-in-rust
geldt:
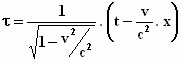
Deze formule bevat venijn: omdat de wortelvorm kleiner is dan één, zou je
denken dat τ groter is dan t.
Als je x constant houdt, klopt dat. Je kijkt dan als het ware telkens
naar nieuwe klokken die vervolgens verdwijnen in de x-richting. De
voorste klok liep achter op de achterste en de achterste, laatst geziene klok
loopt dus voor op de voorste. Het beeld verschuift. De tijd op de opeenvolgende
klokken die je ziet passeren, loopt sneller dan onze
tijd dankzij het verloop van de tijd in het bewegende stelsel.
Als je één klok in de gaten houdt, neemt zijn plaats x toe met v
. t. De term tussen haakjes wordt dan: 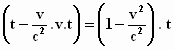
Hiermee wordt Δτ = 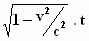 , de formule die we al gezien hadden, de "langzamere tijd"
. Deze is zoals verwacht kleiner dan t. Dan
loopt de klok in het stelsel-in-beweging trager dan in het stelsel-in-rust.
, de formule die we al gezien hadden, de "langzamere tijd"
. Deze is zoals verwacht kleiner dan t. Dan
loopt de klok in het stelsel-in-beweging trager dan in het stelsel-in-rust.
De formule is van groot belang in het verhaal van Einstein. In de volgende
paragraaf zullen we hem opnieuw tegenkomen, maar dan volgen we de afleiding die
Einstein ervoor gaf.
Stap 5: De plaats nog eens bekeken.
We hadden gezien (zie stap 3) dat de voorbijvliegende balk korter
is bij meting dan
dezelfde balk in rust. Omdat elke afstand in gedachten door een balk kan worden
voorgesteld, zal iedere afstand in een bewegend stelsel korter worden bevonden.
De vraag of de balk nou werkelijk korter is, moet met ja
worden beantwoord. De cowboys meten de lengte ℓ en wij meten r
. De balk is niet veranderd, maar hij neemt in bewegende toestand minder lengte
in dan in rust.
Onder stap 3 hadden we voor de lengte van de bewegende balk gevonden:
r = 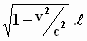
Zoals we eerder hadden gezien , is r = x – v . t
Dus 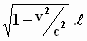 = x
– v . t = x
– v . t
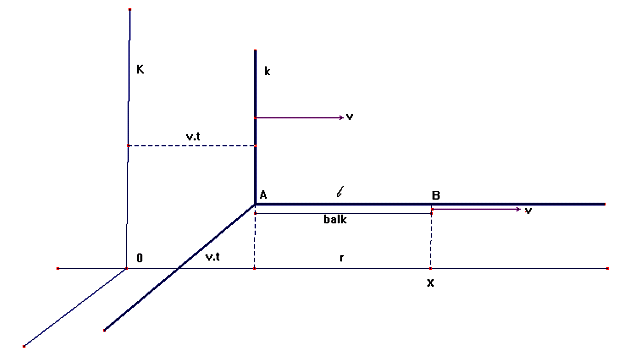
Figuur 2.22 De plaats van het punt B
De lengte ℓ is de plaats van punt B in het bewegende
stelsel en het punt x is de plaats van het punt B in ons stelsel.
Zo vinden we de relatie tussen de plaats van het punt B in ons stelsel en
in het cowboy-stelsel:
ℓ = 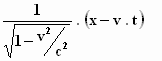
Om de waarden die voor het bewegende stelsel gelden duidelijk te kunnen
onderscheiden van de waarden in het stelsel-in-rust, gebruikt Einstein hiervoor
Griekse letters. Voor de "tijd" was dat de τ
(tau) en voor de "plaats" in de x–richting wordt het de letter ξ
(xi). In het bewegende stelsel mag je dan praten over de ξ–richting
en over de ξ–as van dat stelsel.
Daarmee schrijven we de formule als:
ξ = 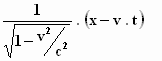
Dit is de tweede , zeer belangrijke formule die Einstein afleidt in zijn
artikel.
Stap 6: Conclusie
We hebben twee belangrijke formules gevonden, waarmee het mogelijk is van een
bepaald punt de plaats ξ en de
tijd τ op de balk te vinden als
je van dat punt de plaats x en de tijd t uit onze waarnemingen
kent:
ξ = 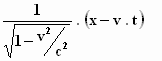 "plaatsformule"
"plaatsformule"
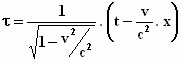 "tijdformule"
"tijdformule"
De twee formules heten officieel de Lorentztransformaties.
Oefening 5
De balk met de cowboys A en B heeft een lengte r (door ons gemeten).
Laat zien aan de hand van de "plaatsformule" dat op het tijdstip
t = 0 , als A zich in ξ
= x = 0 bevindt, de cowboy B zich in het
punt ξ
=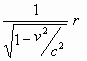 bevindt.
bevindt.
Laat zien aan de hand van de "tijdformule"dat op het tijdstip
t = 0, als A zich in de oorsprong bevindt
(ξ
= x = 0), voor B de tijd geldt volgens de formule “te vlug geschoten"
(zie eerder) volgens de cowboys
(met een minteken omdat de
"tijdformule" ook tot uitdrukking brengt dat B achterloopt).
Terug
|
|
Voorbeeld
We zullen in dit voorbeeld één (met de balken, de cowboys, de klokken en het
licht) vergelijkbare situatie schetsen, maar met veel kleinere snelheden. We stellen
ons een kanaal met stilstaand water voor. Over het kanaal wordt een rechthoekig
raamwerk met een (in rust gemeten) lengte van 100 m voortgetrokken met een
snelheid v = 1,25 m/s (zie figuur 2.23). De constructie beweegt zo lichtvoetig
over het water dat het water niet in beroering komt. Tussen de voorzijde en de
achterzijde van de constructie vaart een bootje heen en weer met een constante
snelheid c = 4 m/s ten opzichte van het water. Tijdens het keren verliest het
geen tijd. In dit systeem wordt met het heen en weer varende bootje de
meetprocedure van Einstein uitgevoerd om te onderzoeken of twee klokken
gelijklopen. Snelheden groter dan 4 m/s voor de constructie worden uitgesloten,
want dan werkt de procedure uiteraard niet meer.
Met de heen en weer varende bootjes hebben we dus een klok gevormd!
Een lengte is dus het product van de tijd en de snelheid van de bootjes.!
Op de achterzijde van de constructie zit cowboy A met zijn klok en aan de beginzijde zit
cowboy B met zijn klok. Binnen de constructie laten de cowboys stiekem een bak water
meeslepen, even lang als het raamwerk, om een eigen bootje met 4 m/s heen en
weer te kunnen laten varen. Dat is niet eerlijk, maar wij doen alsof we van niets
van weten.
Wij staan langs de kant van het kanaal met een goede klok in de hand.
We gaan er van uit dat de tijd τ en de lengte r
in het bewegende stelsel anders zijn dan de tijd t
en de lengte ℓ bij ons.
We plaatsen twee vlaggetjes langs het kanaal op een onderlinge afstand van
eveneens precies 100 m. Als het raamwerk passeert, meten we hoe lang punt B erover doet
om van het eerste tot het tweede vlaggetje te komen. Dit is de 'gewone’
meting en we vinden Δt =
100/1,25 = 80 sec.
Als we cowboy B vragen om de tijd te meten, vindt hij een waarde die gelijk
moet zijn aan Δτ = r
/1,25 sec , want voor hem is de afstand r tussen de vlaggetjes niet op voorhand gelijk aan
100 m terwijl de snelheid waarmee de vlaggetjes hem passeren dezelfde snelheid
is die de constructie heeft ten opzichte van ons: 1,25 m/s.
Van belang is de verhouding Δτ / Δt
= r / 100.
(1)
Hoeveel trager is de tijd in het bewegende stelsel? Om dit te beantwoorden,
bekijken we hoe lang het bootje over de heen- en terugweg tussen A en B doet.
De tijdsduur om van A naar B en terug te geraken, is volgens ons:
Δt =
r / (4–1,25) + r / (4 + 1,25) = r . 0, 5541 sec.
Volgens de cowboys is de benodigde tijd over de heen en terugreis, gemeten
met hun bootje in de stiekem meegesleepte bak met stilstaand water Δτ
= 200/ 4 = 50 sec.
Deze verhouding is dus: Δτ /
Δt = 50 / (r . 0,5541) = 90,23 / r
(2)
Als we de verhoudingen (1) en (2) gelijkstellen, krijgen we:
(r)2 = 90,23
. 100 = 9023
Hieruit volgt r = √(90,23x100) = 94,99 m
Ditzelfde resultaat kunnen we op directe wijze via de formule
"kortere balk" (zie aldaar) krijgen.
Nu kunnen we berekenen (met (1)) welke tijd B meet voor de passage van de
twee vlaggetjes:
Δτ = (94,99 / 100) .
80 = 75,99 sec.
Dat is wel wat anders dan die 80 sec die wij hebben gemeten.

Figuur 2.23 Raamwerk met snelheid v in een kanaal
De tijd verloopt voor B dus duidelijk langzamer. Voor B 75,99 sec en voor ons
80 sec.
We kunnen ons met dit voorbeeld voor ogen ook indenken hoe het achterlopen
van klok B ontstaat:
De raamconstructie ligt oorspronkelijk stil in het kanaal. We gaan uit van
klokken die allemaal gelijklopen en dat willen we controleren voor de situatie dat de
constructie van stilstand tot een zekere snelheid komt. Op het moment het bootje
wegvaart bij A, komt de constructie gelijkmatig versneld in beweging. Als het
bootje bij B aankomt, heeft dit punt snelheid verkregen en heeft zich in die
tussentijd verplaatst. Het bootje moet dus een grotere afstand afleggen dan bij
een stilliggende constructie en doet daar langer over.
Het bootje vaart terug. A komt het bootje al tegemoet, dus de tijd over de
afstand B naar A is minder dan van A naar B. Hieruit moet de conclusie worden
getrokken dat volgens de meting klok B voorloopt, immers, als de klokken
gelijklopen, moet het bootje even lang over de heenweg als over de terugweg
doen.. Als de cowboys hiervoor
corrigeren, dan zien wij klok B achterlopen. We laten het bootje heen en weer
varen tot de constructie zijn eindsnelheid v heeft bereikt. Het is aannemelijk
dat door het optellen van alle beetjes dat B achterliep het tijdsverschil wordt
gevonden volgens de formule "te vlug geschoten":
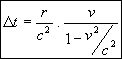 "te vlug geschoten"
"te vlug geschoten"
Dus tijdens de versnelling ontstaat een tijdverschil tussen de voorste en de
achterste klok!
Opmerkingen:
1ste De meetprocedure van Einstein gaat uit van een lichtsignaal
dat in dezelfde richting als de bewegingsrichting van de balk wordt heen en weer
gezonden. Wat nu als het licht loodrecht op de bewegingsrichting
van de balk wordt
uitgezonden? We laten daartoe een balk met een lengte ℓ, waarop zich in de
punten A en B de cowboys bevinden, loodrecht op zijn lengteas
bewegen. De cowboys meten door het lichtsignaal langs de balk
naar elkaar toe te zenden. Van A naar B en weer terug naar A.
De bewegingsrichting van de balk staat dan loodrecht op de
bewegingsrichting van het lichtsignaal, volgens de cowboys.
Zij meten voor de tijd die het licht over de heen– en
terugreis langs de balk doet:
τ = 2. ℓ/c.
Voor ons gebruikt het licht meer tijd (zie figuur 2.24) omdat de afstand van
A naar B* en vervolgens van B* naar A* groter is dan tweemaal de afstand van A
naar B.
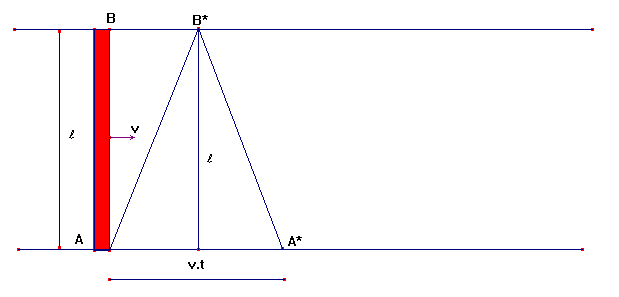
Figuur 2.24 De meetprocedure loodrecht op de bewegingsrichting
De afstand van A naar B* en terug van B* naar A* is 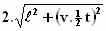 (volgens Pythagoras). De tijd die het licht er voor ons over doet is dus t =
(volgens Pythagoras). De tijd die het licht er voor ons over doet is dus t = 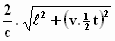 . .
Door beide zijden van deze vergelijking te kwadrateren krijg je:
t2 = (4/c2 ). (ℓ2 + (v . ½t)2
= 4.ℓ2/c2 + v2.t2/c2.
Hiermee wordt t2 . ( 1 – v2/c2) = 4.ℓ2/c2
en t = 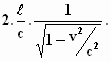
Als je dit vergelijkt met de tijd van de cowboys τ
= 2. ℓ/c, blijkt er uit dat
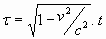 . .
Ook op deze manier blijkt de tijd in het bewegende stelsel langzamer te
verlopen dan in het stilstaande stelsel. We zijn er hierbij vanuit
gegaan dat de afstand AB, de lengte van deze bewegende balk niét verandert,
terwijl hij in de bewegingsrichting wel verandert.
2de Wij constateren dat de tijd langzamer verloopt in het
bewegende stelsel dan in het stelsel-in-rust. Als we de cowboys twee van onze
perfect lopende klokken hebben meegegeven, gaan die dan daadwerkelijk langzamer
lopen? Hoe kunnen we ons dat voorstellen? Dat vraagt nogal wat van je fantasie.
Het is bovendien complex, want vanwege de gelijkwaardigheid van de twee stelsels,
de symmetrie, moeten de cowboys, omgekeerd, ook onze klokken langzamer "zien" lopen.
Kan dat wel? Is dat niet in strijd met elkaar of is het gezichtsbedrog?
Het antwoord luidt uiteraard: "Het is de harde realiteit".
We zullen nu laten zien, aan de hand van een voorbeeld, hoe het mogelijk is
dat wij hun klokken langzamer zien lopen terwijl zij onze klokken
langzamer zien lopen.
We gaan uit van twee zeer lange balken (zie fig. 2.25).
De bovenste lijn 1 is de
stilstaande balk met het nulpunt P in de oorsprong. De tijd voor het hele
stelsel is t = 0.
Lijn 2 stelt de bewegende balk voor met het nulpunt A
in de oorsprong. Deze balk heeft een snelheid v = 0,6.c m/s (= 0,6 maal
de lichtsnelheid) parallel aan de stilstaande balk. De tijd geven we aan met t.
Als P en A elkaar passeren geldt voor beide punten de tijd t =
t = 0 sec. Voor het stilstaande stelsel is
dit de tijd voor het gehele stelsel, voor het bewegende stelsel geldt deze tijd
alleen in het punt A. De tijd in het bewegende stelsel gaat bovendien trager met een factor 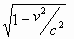 =
0,8. =
0,8.
In het stilstaande stelsel plaatsen we klokken op een afstand van 0,6 . c
meter. Dus iedere hele seconde (in het stilstaande stelsel) passeert het
punt A een volgende klok in het stilstaande stelsel.
In het
stelsel-in-beweging staan ook ten opzichte van A klokken op een
onderlinge afstand van 0,6.c m. Omdat afstanden korter zijn als je ze
beziet vanuit het stelsel-in-rust, is de onderlinge afstand volgens ons
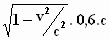 =
= 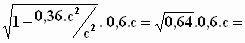 0,8 .
0,6 . c = 0,48 . c meter.
0,8 .
0,6 . c = 0,48 . c meter.
De tijden die de klokken op de bewegende balk aangeven op het moment dat A het
punt P passeert , zijn er bij
geschreven. We spreken af dat op het tijdstip t = 0
ook t
= 0. Het punt B bijvoorbeeld, dat op 0,48.c meter op A
voorligt in de bewegingsrichting, heeft de tijd τ
= – 0,36 seconde. Dit kan vlot worden berekend met de formule "te
vlug geschoten".
 | Voor velen zal het blijven wringen dat de klokken waar verschillende
tijden bij staan geschreven toch gelijklopende klokken zijn. De oorzaak zit
er in dat wij vanuit het stilstaande stelsel de klokken volgens ons
gelijktijdig aflezen, maar volgens de cowboys lezen we ze niet gelijktijdig
af: klok B lezen we 0,36 sec eerder af dan klok A. |
 | Dit brengt ons op de vraag wat de "tijd" van het
bewegende stelsel precies is. Welke klok moeten we daarvoor aflezen. We
spreken af dat de tijd van klok A de tijd van het stelsel-in-beweging
weergeeft. Op het tijdstip t = t
= 0 hebben beide stelsels dezelfde tijd. |
Lijn 3 geeft de situatie aan na 1 seconde. A
passeert dan de klok bij Q, die dan uiteraard 1 seconde aangeeft. Maar de
klok van A is langzamer, die geeft 0,8 seconde aan. Van enige
punten staat de tijd erbij geschreven, te vinden door bij de tijden van de
tweede lijn 0,8 sec op te tellen. Maar voor de "tijd" van
het stelsel-in-beweging geldt de tijd van klok A: de "tijd"
loopt er achter.
Na precies 4 seconde (zie lijn 4) passeert klok A (zie lijn 5)
voor de
vierde keer een klok (R). Die geeft aan: 4 seconde. De klok van A
geeft dan aan 3,2 seconde. Ten bewijze hiervan maken we een flitsfoto,
waar beide klokken op staan als ze elkaar passeren. Klok A loopt achter
op R en dus op alle klokken van ons stelsel, want onze klokken lopen
gelijk. De "tijd" van het bewegende stelsel loopt trager dan
onze tijd.
De situatie vanaf de bewegende balk bekeken, ziet er anders uit (maar
eigenlijk hetzelfde). Als we de bewegende balk (lijn 5) met A
en B als het rustende stelsel accepteren (let op: de schaal in lijn
5 is kleiner dan in lijn 1) en het stelsel met P en Q als
het bewegende stelsel (lijn 6), dan moeten we eerst afspreken wat de"tijd"
voor het stelsel met P en Q is: natuurlijk , zoals we het ook voor
het bewegende stelsel AB hadden afgesproken, de tijd van de klok in
P.
Op het moment dat R het punt A passeert - de gebeurtenis kan niet
worden ontkend, maar het tijdstip waarop dit gebeurde wordt betwist - wijzen de
klokken van het stelsel met A en B het tijdstip t
= 3,2 sec aan. Welke tijd geldt dan voor het stelsel met P en Q?
Dit laatste stelsel heeft nu van plaats tot plaats verlopende tijden, te
berekenen met "te vlug geschoten". Te berekenen is dat de tijd
in P op 2,56 sec uitkomt en die tijd is de "tijd"
voor het gehele stelsel met P en Q. Dus de tijd van het stelsel PQ
loopt achter op de tijd van stelsel AB. Via een flitsfoto vanuit het
stelsel AB als klok P één van de klokken van AB passeert,
is het bewijs te leveren.
 | Wanneer je de tijd van één van de andere klokken als uitgangspunt
voor de "tijd" van het bewegende stelsel neemt, krijg je
hetzelfde resultaat. De boel verschuift wat, maar de verhoudingen blijven
gelijk. |

Figuur 2.25 De klok in het andere stelsel loopt altijd trager.
 | Er zijn allerlei manieren om de tijd te verbeelden als iets wat naar ons toe
of van ons weg stroomt. Als een rivier. De tijd is in beweging en wij ondergaan
de tijd passief. De bewegende balk ligt scheef in de tijdstroom en drijft een
beetje met de tijd mee zodat de tijd langzamer langs de balk stroomt dan langs
ons. Het is een aardige bezigheid om de tijd in beelden te vatten, maar het is
niet eenvoudig een alledaags beeld te vinden dat voldoet aan de eigenschappen
die we er van kennen. In deze uitleg zullen we ons er niet
aan wagen, we blijven gewoon bij de tijd, maar niemand houdt je tegen om de
fantasie de vrije loop te laten! |
Waar we wel aandacht aan zullen besteden, omdat het een goede voorbereiding is
op de beschouwingen bij komende paragrafen, is de weergave van de
lengte van de bewegende balk en de tijd in het stelsel–in–beweging in een
geometrische figuur, de rechthoekige driehoek. De term 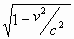 nodigt
daar namelijk toe uit. Bekijk figuur 226, een rechthoekige driehoek waarvan de
schuine zijde de waarde c heeft en de korte zijde de waarde v , dan heeft
de lange rechthoekzijde DF , volgens de stelling van Pythagoras, de waard nodigt
daar namelijk toe uit. Bekijk figuur 226, een rechthoekige driehoek waarvan de
schuine zijde de waarde c heeft en de korte zijde de waarde v , dan heeft
de lange rechthoekzijde DF , volgens de stelling van Pythagoras, de waard
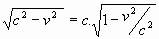 . .
Dus DF
= EF . 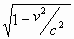 . .
Tussen DF en EF bestaat dezelfde relatie als tussen r en ℓ
in de formule voor de "kortere balk" die we eerder hebben
gezien: r = ℓ . 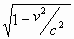
De "kortere balk" heeft een lengte die meetkundig gezien
gewoon de projectie van de schuine zijde op de lange rechthoekzijde is (zie
figuur 226).
In de figuur er naast (fig. 227) zijn de afstanden door c (de
lichtsnelheid) gedeeld. De lange rechthoekzijde heeft dan de lengte 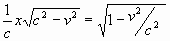 . .
Wanneer je de afstand deelt door de lichtsnelheid c geeft de uitkomst de
tijd weer die het licht over die afstand doet. De driehoek geeft dus tijden
weer .
In deze rechthoekige driehoek gelden voor de onderlinge
verhoudingen van de lengten van de lijnen waar de driehoek uit opgebouwd is:
Schuine zijde : korte zijde : lange rechthoekzijde c : v :
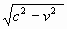 = 1 :
v/c : = 1 :
v/c : 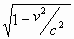 . De
verhouding blijft hetzelfde als alle drie getallen met hetzelfde getal
worden vermenigvuldigd. . De
verhouding blijft hetzelfde als alle drie getallen met hetzelfde getal
worden vermenigvuldigd.
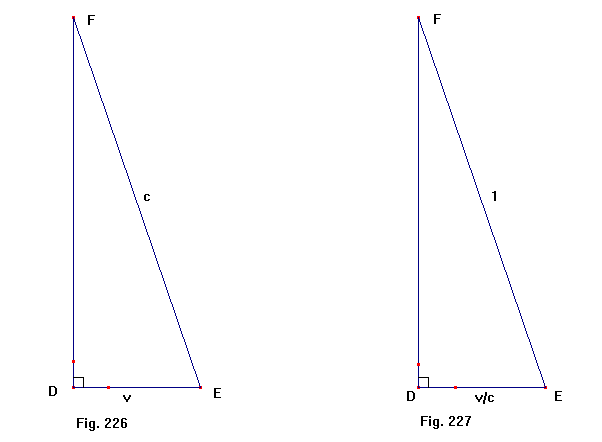
Deze verhouding geldt in iedere driehoek die met de genoemde
driehoeken gelijkvormig is.
Zo’n driehoek zullen we "De driehoek met de bekende
verhoudingen" noemen.
We zoeken uit of we in Figuur 227 ook de formule "te
vroeg geschoten" terug kunnen vinden. We tekenen daartoe de bewegende
balk met de cowboys A en B en de identieke balk-in-rust PQ
(zie blz. 1), waar wij ons op bevinden, in één figuur, figuur 228. De
punten A en P vallen samen, hetgeen betekent dat op het moment dat
A het punt P passeert de tijden in A en P gelijk
worden gezet. Deze twee punten hebben op dat moment dezelfde tijd. De twee
balken maken net zo’n hoek met elkaar als de scherpe hoek in "de
driehoeken met de bekende verhoudingen". Als we vanaf een punt op de
lijn AB een loodlijn neerlaten op de lijn PQ ontstaat er weer zo’n
driehoek met bekende verhoudingen en evenzo als we vanaf PQ een loodlijn
neerlaten op AB.
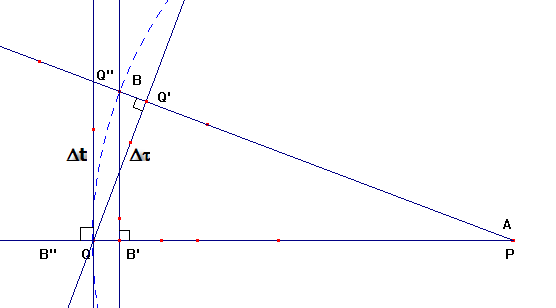
Figuur 228 Twee balken: bewegend AB en in rust PQ
In de hier getekende figuur kan je de verkorting van de
bewegende balk terugvinden als de lengte AB’ , de projectie van AB
op PQ, maar ook de verkorting van de tijd is in deze driehoek terug te
zien. Als we een zekere tijd in het stelsel-in-rust weergeven met de afstand PQ
dan is de benodigde tijd in het stelsel-in-beweging te vinden door de projectie
van PQ op AB te nemen, namelijk AQ’ .
Ook de driehoeken BB’B’’ en QQ’Q’’
zijn driehoeken met de bekende verhoudingen en als je hiervan gebruik maakt, kan
je laten zien dat BB’’/c de formule "te vlug geschoten"
volgens onze klokken weergeeft:
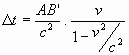
Bedenk dat AB' de lengte voorstelt zoals wij
waarnemen, eerder aangegeven met r.
De formule "te vlug geschoten" volgens de
tragere klokken van de cowboys is terug te vinden in QQ’/c of wat op
hetzelfde neerkomt:BB’/c :
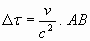
Opmerkingen
 |
Eerder zijn deze
formules ook te vinden, maar daar werd AB’ nog r genoemd en AB
was de lengte ℓ van de balk. |
 |
Het zal duidelijk zijn dat de tekeningen geen
bewijs vormen voor de relativiteitstheorie, ze vormen een illustratie die
verhelderend kan werken |
 | Einstein heeft een hoop verwarring teweeggebracht door zijn ontdekking
dat de tijd van het stelsel-in-rust en de tijd van het stelsel-in-beweging
van elkaar verschillen. Wij moeten in gedachten houden dat de tijd (en ook
de lengte), gezien door de cowboys, in het stelsel-in-beweging volstrekt
normaal zijn, voor hen bevinden ze zich in het stelsel-niét-in-beweging en zijn wij het
stelsel-niét-in-rust. De verschillen komen tot uiting als we vanuit een
stelsel-in-rust de tijd en de lengte in een stelsel-in-beweging waarnemen:
Als de cowboy in de lengterichting van de balk een dutje doet, zeggen we
vanaf de grond: "Het is toch maar een kort mannetje", en als we op
zijn horloge kijken, zeggen we: "Dat klopt niet, dit horloge loopt te
langzaam". De lengte is korter, de bewegende balk past ruim tussen twee
afstandsstrepen die de lengte aangeven van een stilstaande identieke balk.
De tijd is echter langer want een verschijnsel (bijvoorbeeld het heen en
weer slingeren van de klepel van een klok) dat zekere tijd vraagt, is nog
niet afgerond in het bewegende stelsel als de tijd volgens ons al op is. De
tijd hiervoor past niet in de tijd die wij ervoor hebben gereserveerd. Hun
lengte neemt minder ruimte, maar hun tijd neemt meer ruimte in beslag. |
Oefening 6
We zullen nog wel vaker die
rechthoekige driehoek terugzien met de verhoudingen: c "staat tot" v
"staat tot" √(c2 – v2) . Korter
geschreven als c : v : √(c2 – v2) .
De"driehoek met de bekende verhoudingen".
De stelling van Pythagoras werd er op de middelbare school
ingedreund als: a2 + b2 = c2, waarbij a en b de
lengten van de rechthoekzijden waren en c de lengte van de schuine zijde. De
lengten verhouden zich dus als a : b : c .
 |
Laat zien dat deze verhouding ook geschreven kan worden als
a/c : { √(c2
– a2)}/c : 1. |
Hierbij is de lengte c gelijk aan één gesteld. Je mag
natuurlijk ook a of b op 1 stellen, dan komt er in de plaats van de eerste term een 1 te
staan of in de plaats van de tweede term.
 |
Een bekende verhouding voor een rechthoekige driehoek is 3 :
4 : 5. Klopt Pythagoras? |
 |
Als we de lengte 5 op één stellen, bereken dan de term met
het wortelteken en laat zien dat daar 4/5 uitkomt. De andere zijde heeft dan het
verhoudingsgetal 3/5. Stel dat deze laatste zijde een echte lengte heeft van 50
cm, laat dan zien uit de verhoudingen dat de andere zijden de lengten 66,7 cm en
83,3 cm hebben. |
Is de balk echt korter?
Om op deze vraag een definitief antwoord te geven, beschieten
we de passerende balk met twee kanonnen die op een geringere afstand van elkaar
staan dan de lengte van de balk. De kannonnen schieten hun kogels loodrecht
omhoog. De balk is 100 meter lang en de snelheid van de balk is 0,8 x de
lichtsnelheid c m/s, zodat wij hem waarnemen met een lengte van 60
m (immers √(1–0,82) = 0,6). We zetten de kannonnen op
een afstand van iets meer dan 60 m, maar lang geen 100 m. Op het
moment dat de balk passeert, schieten we tegelijkertijd de twee kannonnen af.
Het kan geen kwaad volgens ons, want de voorste kogel zal voorlangs gaan en de
achterste zal achterlangs gaan. Dat is precies wat we waarnemen: ze vliegen
tegelijkertijd langs de balk op een onderlinge afstand van iets meer dan 60 m.
De balk wordt niet geraakt!
Wat vinden de cowboys daar nou van. Deze onverschrokken
jongens kijken niet op van een kogel meer of minder. Het enige wat hen
verbijstert, is dat wij zo mis konden schieten. Voor open doel! De kannonnen
staan immers op een onderlinge afstand van maar net 36 m volgens de cowboys.
Want ook voor hen geldt weer dat √(1–0,82) = 0,6, dus
onze 60 m is voor hen 0,6 x 60 m = 36 m, terwijl hun balk 100
m is. Hoe kregen wij het voor elkaar! Nou, dat hebben ze best gezien: het
voorste kanon schoot net te vroeg en het achterste kanon schoot net te laat.
Hier geldt weer de formule "te vlug geschoten".
Volgens de
cowboys
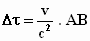
Als je dit invult met v = 0,8 x c en AB = 100 m,
krijg je Δτ = 80/c seconde.
In die tijd legt de balk precies v x Δτ
= 64 m af. Samen met de 36 m die de kannonnen uit elkaar
staan, levert dat 100 m op. Zij zagen op zeker moment de voorste kogel
vlak voorlangs gaan en 80/c seconde later de tweede kogel net achterlangs
gaan..
"Die kunnen niet schieten!", zullen ze denken..
Als we volgens de cowboys de twee kogels gelijktijdig hadden
afgeschoten, zouden ze op een afstand van 36 m van elkaar in de balk zijn
gedrongen, maar dat is niet waar het om ging. Als je de juiste momenten
uitkiest kan je de kogels ook op dezelfde plek in de balk schieten. Het ging er
om of je uit twee kannonnen, die maar 60 m van elkaar afstonden,
tegelijkertijd twee kogels op een balk van 100 m lengte af kon schieten
waarbij de kogels voor en achterlangs zouden gaan. Het antwoord is ja. De balk
is volgens ons echt maar 60 m.
 |
Een directe verificatie van de verkorting van de lengte (de
zogenaamde "Lorentzcontractie") is bij mijn weten nooit
gevonden. Er zal gezocht moeten worden naar een verkleinde botsingsdoorsnede van
zeer snelle deeltjes waar van opzij andere deeltjes tegenaan worden geschoten. |
 |
Oproep: Als iemand hier meer over weet, meld het dan aan het
Einsteingenootschap, opdat het in de tekst kan worden verwerkt.
 |
In 10 jaar tijd heeft nog nooit
iemand een schijn van bewijs gemeld, dus is dit verschijnsel zeer
twijfelachtig.
|
|
Oefening 7
Er suist een balk met een lengte van exact 1000 km door het
heelal met een snelheid van 240.000 km/s (4/5 de van de lichtsnelheid). Voorop
zit cowboy B en achteraan zit cowboy A. De balk scheert vlak langs de aarde en
wij meten zijn lengte.
 |
Toon aan met de formule "Kortere Balk!" dat de
lengte die wij meten gelijk is aan: 600 km! |
Beide cowboys laten hun klokken precies gelijk lopen met de
klokken op aarde.
 |
Bereken met de formule "Te vlug geschoten" dat
cowboy A de klok van B met 4,44 duizendste seconde voor vindt lopen. |
Niet iets om je druk over te maken.
Oefening 8
Een voorwerp met een lengte (in rust gemeten) van 100 meter
suist in zijn lengterichting voorbij de aarde met een snelheid van tweetiende
van de lichtsnelheid. De gezagvoerder laat ons groeten via lichtflitsen die hij
naar eigen zeggen iedere 0,1 sec afvuurt.
Welke lengte heeft het voorwerp voor de aardbewoners en
hoeveel tijd zit er voor hen tussen de opeenvolgende lichtflitsen? Gebruik de
formules "kortere balk"en "langzamere tijd".
Opmerking: Houd de afstand van het voorwerp tot de aarde
constant. De effecten die het gevolg zijn van het naderen of het zich
verwijderen van het voorwerp leiden er toe dat het voorwerp er bij nadering
langer uitziet en bij het zich verwijderen korter, omdat het licht van het verst
verwijderde punt van het voorwerp eerder moet zijn uitgezonden dan van het meest
nabije punt. Voor de lichtflitsen geldt dat ze bij nadering sneller binnenkomen
en bij het zich verwijderen trager. Bij de gevraagde berekening gaat het niet om
deze effecten!
Antwoorden: 97,98 m en 0,10206 sec
Zullen we maar even pauzeren?
Het begint me te duizelen!
Terug
|
|