|
Bijlage bij §5 "Somtekening"
Naar Uitleg §6 Maxwell
Naar Uitleg §5 Optellen
Naar Uitleg Inhoud
Naar Centrale Hal
We zoeken een methode om de "optelformule" meetkundig voor
te stellen. Wat je daarvoor moet weten van de meetkunde is:
 |
de stelling van Pythagoras voor een rechthoekige
driehoek (zie fig. 511). Als de twee rechthoekszijden gegeven zijn, a en b,
is de schuine zijde: √(a2 +b2) |
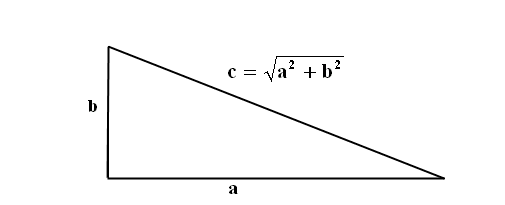
Figuur511 Stelling van Pythagoras: a2 + b2
= c2.
 |
de gelijkvormigheid van driehoeken. Als twee driehoeken
dezelfde hoeken hebben zijn ze gelijkvormig. In fig. 512 bijvoorbeeld is de
grote rechthoekige driehoek ABC gelijkvormig met de kleine rechthoekige
driehoek PBQ |
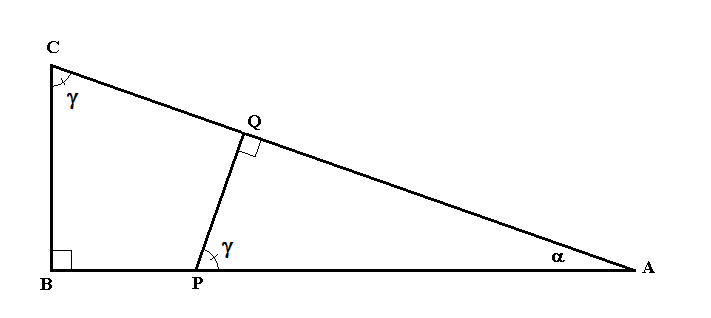
Figuur 512 Twee gelijkvormige driehoeken ABC en QBP
 |
als je een driehoek tekent in een cirkel (zie fig. 513)
met de middellijn PQ als basis van de driehoek en het derde punt van de
driehoek R op de cirkel, dan is de hoek bij het derde punt altijd 90°, dus
PQR is dan een rechthoekige driehoek |
 |
In een rechthoekige driehoek (zie dezelfde figuur) is
het kwadraat van de hoogtelijn h gelijk aan het product van de lijnstukken a
en b waarin de hoogtelijn de basis verdeeld |
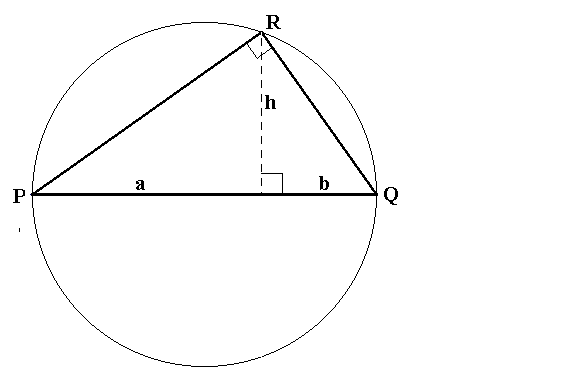
Figuur 513 Rechthoekige driehoek in een cirkel met hoogtelijn h.
In het artikel van Einstein komt geen enkele tekening voor. Een modern mens
wil zich toch iets kunnen voorstellen bij zo’n theorie en daarom zijn de
Lorentzdiagrammen voor "Verleden, heden en toekomst" in §4plus zo
geslaagd. Ze intrigeren en brengen een mens op nieuwe ideeën.
Onze uitdaging was de "optelformule" :
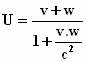
in een tekening weer te geven.
Een trapezewerker heeft het gemakkelijker!
Laten we de formule eens analyseren! Om het ons te vergemakkelijken drukken
we alle snelheden uit in de lichtsnelheid, dus v en w zijn
getallen tussen –1 en +1 en met name c = 1 . Je krijgt dan:
U = 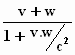 met c = 1
geeft dit
met c = 1
geeft dit
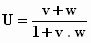
We kunnen deze formule op allerlei manieren herschrijven. Twee mooie vormen
zijn:
U = 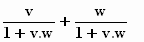 en
U =
en
U = 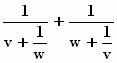
Hierin is wel heel duidelijk te zien dat de snelheden v en w
verwisselbaar zijn, ze zitten symmetrisch in de formule, Einstein zei het al.
Verder zitten er hyperbolen in! De functie f(x) = 1/x is een
hyperbool. Dat biedt de mogelijkheid iets te tekenen (fig.516). In de
figuur tekenen we een hyperbool y = 1/x , de gebogen lijn.
Als we een v uitzetten langs de x–as kunnen we de waarde 1/v
vinden door recht omhoog een lijn te trekken tot de hyperbool en daarvandaan een
horizontale lijn tot de y–as . Hetzelfde gaat op voor de snelheid w
, waarbij we voor de duidelijkheid met w langs de y–as starten.
Met een passer kan je de afstanden die je vindt, optellen en zo kan je som U
construeren. Het is een heel gedoe, maar het klopt. In de figuur is een
voorbeeld gegeven voor de snelheden v = 0,6 en w = 0,8 .
Wanneer je de pijltjes volgt, kom je via de hyperbool van v op 1/v ,
daar tel je w bij op. Vanuit het gevonden punt (w + 1/v) ga je
weer via de hyperbool (volg de pijltjes) naar 1/(w+1/v) en die waarde kan
je aflezen: ongeveer 0,41 . Op identieke wijze bepaal je 1/(v+1/w)
en je leest af: ongeveer 0,54. De som komt uit op ongeveer 0,95 (keer
de lichtsnelheid), in overeenstemming met de formule, waarmee je berekent U =
0,946.
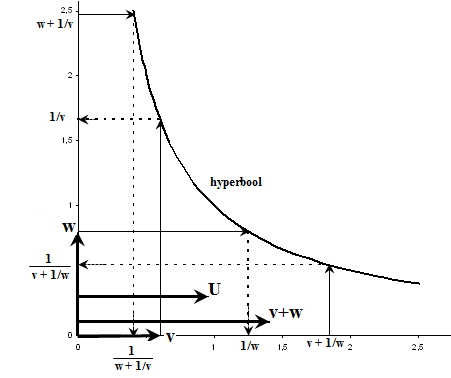
Figuur 516 De som U geconstrueerd met behulp van een hyperbool
Dit maakt een mens al een beetje gelukkig. Het is een illustratie, fysisch
tamelijk ondoorzichtig, maar beter iets dan niets.
We blijven nog even natafelen over de formule 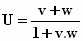 .
Zo’n simpele formule moet toch simpel zijn weer te geven. Opeens ziet iemand
dat alle termen die erin voorkomen ook in het product (1+v) . (1+w) = 1 + (v+w)
+ v.w zijn terug te vinden. Een lichte opwinding maakt zich van ons meester.
Daar moet een diepere betekenis achter zitten! Daar kunnen we iets mee. .
Zo’n simpele formule moet toch simpel zijn weer te geven. Opeens ziet iemand
dat alle termen die erin voorkomen ook in het product (1+v) . (1+w) = 1 + (v+w)
+ v.w zijn terug te vinden. Een lichte opwinding maakt zich van ons meester.
Daar moet een diepere betekenis achter zitten! Daar kunnen we iets mee.
In fig. 517 laten we zien hoe je het product (1+v) . (1+w) in
de vorm van rechthoeken kan weergeven. De snelheden v en w zijn
willekeurig gekozen tussen 0 en +1. Het getal één wordt gevormd door de
oppervlakte van een vierkant met zijden één. De snelheden v en w
zetten we uit langs de X–as en langs de Y–as. De rechthoek met
de zijden 1+ v en 1+w kunnen we verdelen in vier rechthoeken met
de oppervlakten 1 en v.w (met grijs aangegeven) en de oppervlakten
v en w (wit). Uit dit plaatje zie je nogmaals dat v en w
precies dezelfde rol spelen in de formule. De verhouding van de witte
oppervlakte tot de grijze oppervlakte geeft de getalswaarde van de
relativistische som U van twee snelheden volgens de relativiteitstheorie,
waarbij de snelheden zijn uitgedrukt in de lichtsnelheid.
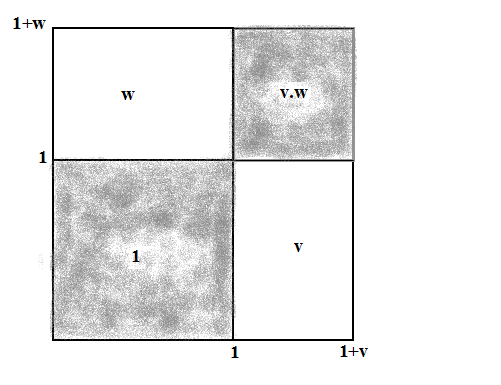
Figuur 517 Presentatie van de optelformule via rechthoekige oppervlakten
Uit deze presentatie kan je ook goed zien dat de verhouding altijd één
wordt indien v of w gelijk is aan 1 , dat wil zeggen: de
lichtsnelheid heeft.
Maar wat gebeurt er als de ene snelheid de andere kant op is gericht als de
andere? Dan moet je de kleinste van de snelheden negatief kiezen. Je kan dan
afspreken dat de oppervlakte w en de oppervlakte v.w negatief
genomen moeten worden, maar de figuur wordt dan ingewikkelder.
Terug
 |
Oefening 25
Probeer op een vergelijkbare manier als in figuur 517 een diagram te
construeren waarbij w negatief is ten opzichte van v |
Nu we een beetje warm zijn gelopen, kunnen we een illustratie (figuur 518)
laten zien die gebaseerd is op de driehoek met de bekende verhoudingen. Ten
opzichte van de verticale lijn met van P tot Q een lengte één,
die de lichtsnelheid voorstelt, zetten we twee willekeurige snelheden v
en w (kleiner dan de lichtsnelheid) langs de horizontale as in
tegengestelde richting uit. De afstand AB heeft dus de lengte v + w
. Die hoeven we alleen maar door 1+v.w te delen om de somsnelheid U
te krijgen.
Je weet nog dat U = 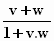 .?
Vandaar dus! .?
Vandaar dus!
Maar hoe teken je dat met passer en liniaal!?
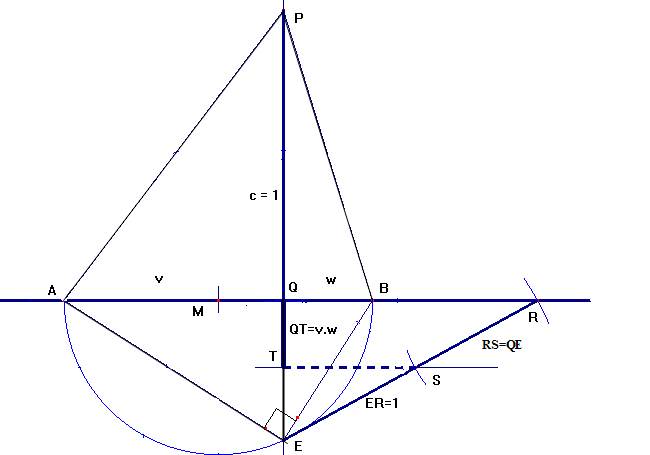
Figuur 518 Eerste stappen om U te construeren
Met een passer construeren we het midden M van de lijn AB .
Rond dit punt trekken we een cirkel door A en B. Deze snijdt de
verticale lijn (het verlengde van PQ) in E.
Dan is ABE een rechthoekige driehoek. In deze rechthoekige driehoek
geldt voor de hoogtelijn EQ (de loodlijn van E op AB) het
volgende: (EQ)2 = v . w .
We zoeken een lijn met de lengte 1+ v . w . De afstand PE is
1 + EQ = 1 + √ (v.w) . Dat lijkt er al verdraaid veel op, maar dat
wortelteken moet er uit.
De lijn EQ heeft de lengte √(v.w) maar we zoeken een lijn
met de lengte v . w.
Is het mogelijk om in de tekening een lijn te trekken waarvan de lengte het
kwadraat is van de lengte van EQ , met andere woorden: kan je een lijn
kwadrateren?
Ja, dat kan als volgt: trek een lijn naar het punt R op de horizontale
as op een afstand één (even lang als PQ) van E. Vervolgens pas
je met de passer de afstand EQ af vanuit R langs RE. Het
punt dat op een afstand EQ van R ligt, noemen we S .
Vanuit S laten we een loodlijn neer naar het punt T op EQ.
De driehoek STE is gelijkvormig met RQE en daarom is de verhouding
QT/EQ dezelfde als RS/RE. Omdat RS = EQ volgt eruit QT/EQ
= EQ/RE dus QT = (EQ)2 / RE. Omdat RE = 1
volgt er uit: QT = (EQ)2.
Zo vinden we dus het kwadraat van de lengte van EQ.
Dat is de afstand die we zoeken: QT = v . w. Hiermee wordt PT
gelijk aan 1 + v . w . We hadden al het lijnstuk AB = v + w .
We komen nu tot de vraag hoe je twee lijnstukken op elkaar kunt delen om de
waarde van U te construeren:
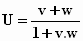 . .
Dat kan als volgt (zie figuur 519):
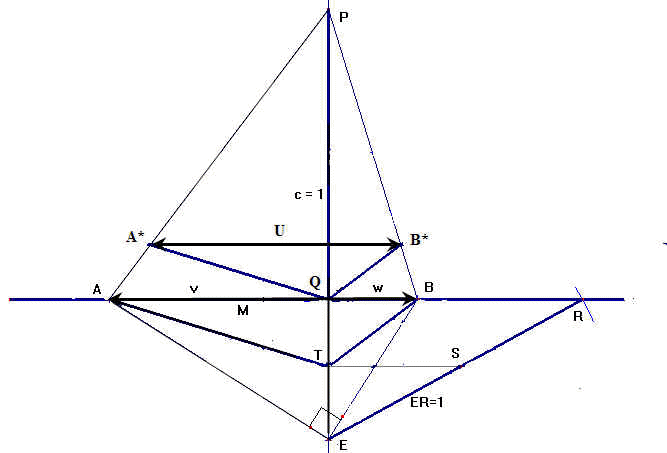
Figuur 519 De constructie van U door deling met (1+v.w)
We construeren een driehoek A*B*P waarin de afmetingen (1+v.w)
maal zo klein zijn als in de driehoek ABP.
Trek eerst het lijntje TB. Daarna vanuit Q een lijn evenwijdig
aan TB tot het snijpunt B* . Wegens de gelijkvormigheid van de
driehoeken BTP en B*QP is B*P inderdaad (1+v.w) keer
zo klein als BP omdat PT zo is geconstrueerd dat deze afstand (1+v.w)
keer groter is dan PQ.
We vinden A* door vanuit B* een lijn evenwijdig aan BA
te trekken tot deze PA snijdt.
De afmetingen van A*B*P zijn dus (1+v.w) keer zo klein als van ABP
, precies zoals gewenst.
Dan is ook A*B* = 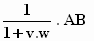 .
Met AB = v + w volgt A*B*
= U = .
Met AB = v + w volgt A*B*
= U = 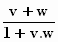 . .
Dat is wat we zochten.
Uit de tekening is op te meten, door de lengte van AQ te delen door de
lengte van PQ, dat v = 0,756. c en w = 0,306 . c . We meten
via de lengte van A*B* uit de tekening voor U = 0,863. c .
Als we dit controleren met de formule, krijgen we: 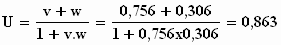 Dit zegt genoeg!
Dit zegt genoeg!
Intermezzo!
Deze
volgende oplossing werd ons in augustus 2014 toegezonden door Jan
van der Heijden uit Maarn.
Hij
is uitgegaan van zijn stelling dat voor de relativistische
som U geldt :
U
/ (v+w) = γv x
γw /
γU .
Hierin
betekent γv
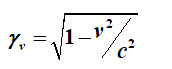
Voor
γw en
γU
geldt iets vergelijkbaars
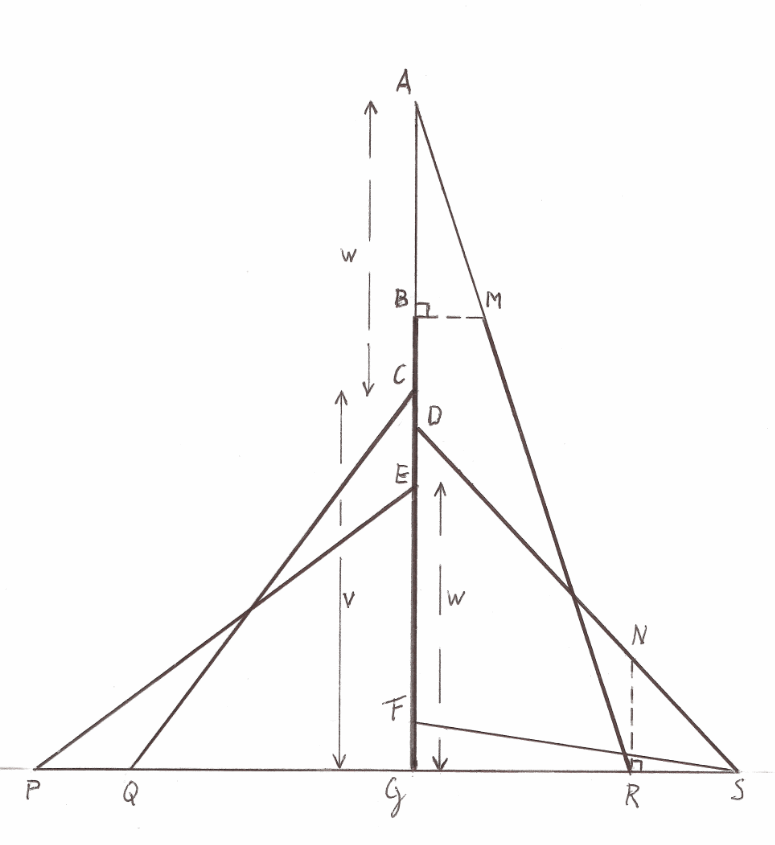
De
vette lijn BG is de voorstelling van de somformule.
De
dikke lijnen QC en PE hebben de lengte c, evenals SD en RM.
Verder
is CG = 0,8xc en AC
= EG = 0,6xc.
Voor
de constructie met passer en liniaal geldt FG = ½xPQ en
FS = QG + FG.
Vanuit
S wordt dan het punt D gevonden omdat SD = c.
Vervolgens
wordt de afstand DN uitgezet, want die is gelijk aan GS.
Vanuit
N een loodlijn op GS levert R.
Langs
de lijn RA wordt de afstand c afgepast om M te vinden.
Vervolgens
een loodlijn op AG geeft B.
Deze
stelling van Jan klopt. Reken maar na (is wel even
puzzelen!).
QG
= c/γv en
PG = c/γw (driehoeken
met de bekende verhoudingen).
Er
geldt GS/GR = DS/DN. Daaruit volgt GS² = c x GR.
PG
x QG = GS² = c x GR (zie de aantekeningen bij deze figuur
en de uitleg bij figuur 518)
U
/ (v+w) = γv x
γw /γU ,
dus U x γU = c²
x AG / (PGxQG) = c x AG/GR. Dus AG/GR
= U/(c/γU).
Dit
betekent dat driehoek AGR een rechthoekige driehoek is met
de bekende verhouding tussen U en c.
U/c = AG/AR =
BG/MR = BG/c.
Hieruit volgt: U =
BG.
Kortgeleden (oktober 2017) kregen we tekeningen
toegezonden van Walter Laukens die deze al lang geleden had uitgewerkt.
Bijzonder fraai is dit exemplaar:
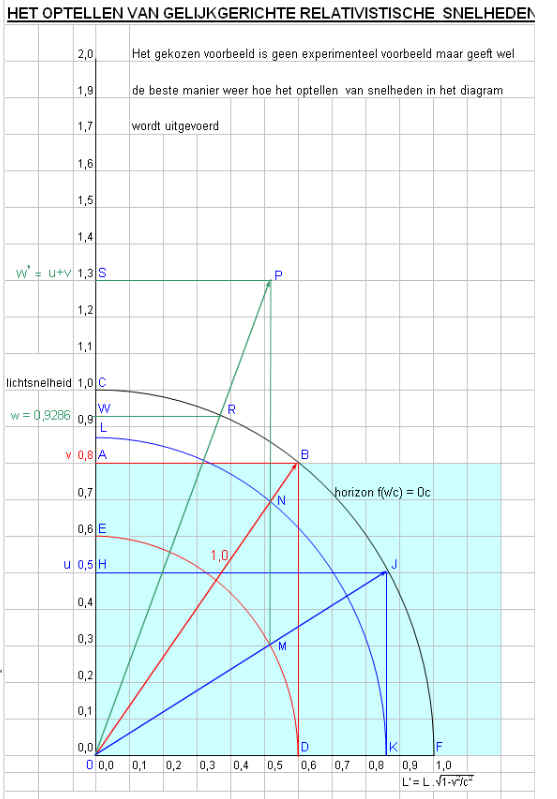
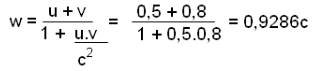 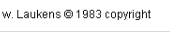
Al deze vrolijke tekeningen hebben geen fysische betekenis. Ze zijn er voor
het plezier en ze ondersteunen het voorstellingsvermogen. Maak je geen zorgen
als je desondanks nog steeds geen goed beeld van de ruimte en de tijd onder
relativistische omstandigheden voor ogen hebt. Wanneer dat eenvoudig was, zouden
geleerden vanuit hun voorstelling van de fysische wereld tot weidse, nieuwe
theorieën kunnen komen, maar de praktijk wijst uit dat vernieuwingen meestal
een gevolg zijn van het moeizaam verder uitpluizen van de formules en van het
verwerken van de resultaten van laboratoriumproeven en andere waarnemingen.
De grootheid van Einstein was dat hij autonoom een nieuw inzicht in de
natuurkunde ontwikkelde dat niet gebaseerd was op experimenten of een vergaand
wiskundig onderzoek. Er waren slechts experimenten (Michelson) die de bestaande
ideeën niet bevestigden! Vanwege zijn uitzonderlijke, natuurkundige
inzicht kon Einstein een reeks voorspellingen doen over verschijnselen waarvan
men soms het bestaan nog niet vermoedde!
 |
Oefening 26
Probeer de somsnelheid van twee relativistische snelheden te construeren,
waarbij de hoogste snelheid positief en de laagste snelheid negatief is. |
Terug
Naar Uitleg §6 Maxwell
|