§ 2. Over de
relativiteit van lengten en tijden.
De volgende
beschouwingen zijn gebaseerd op het relativiteitsprincipe en op het principe
van de constante lichtsnelheid. Deze beide principes zullen we op de
volgende wijze definiëren.
1.
De wetten waaraan de veranderingen van de fysische toestanden van een
natuurkundig verschijnsel voldoen, zijn onafhankelijk van de keuze
van het stelsel, van twee onderling in eenparige
translatiebeweging verkerende coördinatenstelsels, ten opzichte waarvan deze
veranderingen worden beschouwd.
2.
Iedere lichtstraal beweegt zich in het coördinatenstelsel-in-rust met de
vaste snelheid c , waarbij het niet uitmaakt of deze lichtstraal van
een voorwerp-in-rust of van een voorwerp–in-beweging afkomstig is. Hierbij
geldt
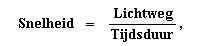
waarbij "tijdsduur"
moet worden opgevat in de betekenis die uit de definitie van
"tijd" van § 1 volgt.
We
gaan uit van een in rust zijnde, onvervormbare staaf; deze heeft, gemeten
met een eveneens in rust zijnde meetlat, de lengte l . We
stellen ons nu voor dat de as van de staaf langs de X-as van het
coördinatenstelsel-in-rust wordt gelegd en dat we de staaf daarna
evenwijdig aan de X-as in een eenparige translatiebeweging (met een
snelheid v) in de richting van de positieve X-as brengen. We vragen ons nu af wat de lengte
is van deze bewegende staaf en we kunnen bedenken dat er twee
methoden zijn om een antwoord op deze vraag te verkrijgen:
a)
De waarnemer beweegt, tezamen met de genoemde meetlat, mee met de te
meten staaf en meet op directe wijze de lengte van de staaf door de meetlat
er langs te leggen, op dezelfde manier als toen de staaf, de
waarnemer en de meetlat zich nog in rust bevonden.
b)
De waarnemer bepaalt met behulp van (overeenkomstig §1 gelijklopende)
klokken–in–rust, die in het stelsel-in-rust staan opgesteld, in welke
punten van het stelsel-in-rust op zeker tijdstip t zich het beginpunt
en het eindpunt van de staaf bevinden. De
afstand tussen deze beide punten, gemeten met de eerder benutte meetlat,
maar nu in rust, is ook een lengte die men als "de lengte van de
staaf" mag beschouwen.
Uit
het relativiteitsprincipe volgt dat de lengte volgens methode a), die
we "de lengte van de staaf in het stelsel-in-beweging" zullen
noemen, gelijk moet zijn aan de lengte l van de in rust zijnde
staaf in het stelsel-in-rust.
Als
we nu op basis van onze beide principes de lengte bepalen volgens de methode
b) , die we "de lengte van de bewegende staaf in het
stelsel-in-rust" zullen noemen, dan zullen we vinden dat deze lengte
van l verschilt.
In
de kinematica gaat men er gewoonlijk stilzwijgend vanuit dat de lengten die
via de beide vermelde methoden worden bepaald, precies aan elkaar gelijk
zijn, met andere woorden dat een bewegend, onvervormbaar voorwerp op
zeker tijdstip geometrisch gezien volledig door hetzelfde voorwerp,
als het op de betreffende plaats in rust zou zijn, kan worden vervangen.
We
stellen ons verder voor dat op de beide uiteinden (A en B) van
de bewegende staaf klokken zijn aangebracht, die gelijklopen met de klokken
van het stelsel-in-rust, dat betekent dat hun tijdaanwijzing op iedere
plaats waar ze zich ook mogen bevinden, steeds overeenkomt met de "tijd
van het stelsel-in-rust"; deze klokken zijn dus "gelijklopend met
die van het stelsel-in-rust".
We
stellen ons vervolgens voor dat zich bij elke klok een met de klok
meebewegende waarnemer bevindt en dat deze waarnemers de in §1
voorgeschreven meetmethode op de twee klokken toepassen om vast te stellen
of de beide klokken gelijklopen. Ten tijde2)
tA
laat de waarnemer in A een lichtstraal uit A vertrekken, die
ten tijde t B in B wordt gereflecteerd en ten tijde
t’A in A terugkomt. Rekening houdend met het
principe van de constante lichtsnelheid vinden we:
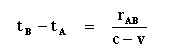
en
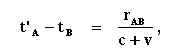
waarbij rAB de lengte
van de bewegende staaf is, gemeten in het stelsel-in-rust. De
meebewegende waarnemers zullen dus constateren dat de klokken niet
gelijklopen, terwijl de waarnemers in het stelsel-in-rust zullen
verklaren dat de klokken wel degelijk gelijklopen.
We
zien dus dat we aan het begrip gelijktijdigheid geen absolute
betekenis mogen toekennen, maar dat twee gebeurtenissen, die vanuit het ene
coördinatenstelsel bezien, gelijktijdig zijn, niet meer als gelijktijdige
gebeurtenissen zijn op te vatten als ze worden beschouwd vanuit een ander,
ten opzichte van het eerste, bewegend stelsel.
Voetnoot:
2) "Tijd"
is hier de "tijd van
het stelsel-in-rust" en dat is tegelijkertijd de "tijdaanwijzing
van de bewegende klok op de plaats waar de klok zich dan bevindt".
|