§ 3. Theorie van de
coördinaten– en tijdtransformatie van een stelsel-in-rust naar een
stelsel dat in een eenparige translatiebeweging verkeert.
We stellen ons voor dat zich in de "rustende"
ruimte twee coördinatenstelsels bevinden, dat wil zeggen twee systemen die
ieder uit drie, loodrecht op elkaar staande, uit één punt komende, volkomen onbuigzame rechte lijnen van een bepaald materiaal bestaan. De X-assen
van beide stelsels laten we samenvallen en hun Y- assen zijn
onderling parallel, evenals de Z-assen. Aan ieder stelsel
wordt een onvervormbare meetlat en een aantal klokken meegegeven. De
meetlatten en klokken van beide stelsels zijn precies gelijk aan elkaar.
Er wordt nu aan het beginpunt van één van de beide
stelsels (het stelsel k) een constante snelheid v
in de richting van de positieve X-as van het andere, het
stelsel-in-rust (aangeduid met K) gegeven. De snelheid v
wordt ook aan de coördinatenassen, de betreffende meetlat alsmede
de klokken overgedragen. Ieder tijdstip t van het
stelsel-in-rust K komt dan overeen met een bepaalde positie
van de assen van het bewegende stelsel en uit symmetrieoverwegingen zijn we
gerechtigd aan te nemen, dat de beweging van stelsel k van
dien aard is dat de assen van het bewegende stelsel op ieder tijdstip t
(met "t" wordt altijd de tijd van het
stelsel-in-rust bedoeld) parallel aan de assen van het stelsel-in-rust zijn.
We stellen ons verder voor dat de ruimte zowel vanuit het
stelsel-in-rust K met behulp van de aldaar aanwezige meetlat
kan worden opgemeten, als vanuit het bewegende stelsel k met
behulp van de met dat stelsel meegegeven meetlat, zodat voor ieder punt de
coördinaten x, y, z (in stelsel K) of de
coördinaten ξ , η, ζ (in stelsel k)
kunnen worden verkregen. Verder wordt met behulp van de in het
stelsel-in-rust opgestelde klokken via lichtsignalen, op de in § 1
aangegeven wijze voor alle punten waar zich klokken bevinden, de tijd t
van het stelsel-in-rust bepaald. Voor het stelsel-in-beweging wordt
eveneens de tijd τ bepaald door, voor alle punten van dit
stelsel waar klokken zijn opgesteld - die ten opzichte van dit stelsel in rust
zijn - dezelfde methode met lichtsignalen toe te passen tussen de punten
waar de genoemde klokken zich bevinden.
Bij ieder stel waarden voor x, y, z, en
t, waarmee de plaats en de tijd van een gebeurtenis in het
stelsel-in-rust exact wordt vastgelegd, behoort een stel waarden voor ξ
,
η, ζ en τ, waarmee zo’n
gebeurtenis ten opzichte van het stelsel k wordt vastgelegd,
en het komt er nu op aan de vergelijkingen te vinden die deze waarden met
elkaar in verband brengen.
Het is zonder meer duidelijk dat de vergelijkingen lineair
zullen moeten zijn vanwege de eigenschap van homogeniteit die we aan ruimte
en tijd toeschrijven.
We gaan uit van een punt dat in het stelsel-in-beweging k
in rust is. In het stelsel-in-rust K heeft het de coördinaten
x, y, z. Wanneer we schrijven x’ = x – v.t
dan moet het stel waarden x’, y, z onafhankelijk van de tijd
zijn.
Eerst bepalen we τ als functie van x’,
y, z en t. Dit doen we door de vergelijkingen te
zoeken waaraan τ voldoet als τ de
tijdsaanwijzing representeert van de in het stelsel k
opgestelde klokken, die
volgens de meetprocedure van § 1 gelijklopen.
Vanuit het beginpunt van stelsel k wordt
een lichtstraal op het tijdstip τ0 langs de X-as
naar x’ gezonden en daarvandaan op het tijdstip τ1
naar de coördinatenoorsprong teruggekaatst, waar hij op het tijdstip τ2
aankomt; er moet dan gelden:
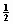 .
(τ0 + τ2) = τ1
.
(τ0 + τ2) = τ1
Als men vervolgens τ als functie van x’,
y, z en t schrijft en de uitdrukkingen voor de
argumenten invult, waarbij het principe van de constante lichtsnelheid in
het stelsel-in-rust wordt toegepast, verkrijgt men:
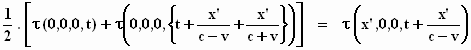
Hieruit volgt, als men x’ oneindig klein
neemt:
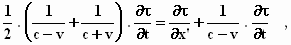
of
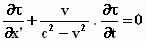
Merk op dat we in plaats van de coördinatenoorsprong
ieder ander punt als uitgangspunt voor de lichtstraal hadden kunnen nemen en
daarom geldt de laatst verkregen vergelijking voor iedere waarde van x’,
y, z.
Als men een gelijksoortige redenatie toepast op de
richtingen van de Y-as en de Z-as en bedenkt dat
het licht – gezien vanuit het stelsel-in-rust – zich in beide gevallen
met de snelheid 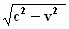 langs de genoemde
assen voortplant, verkrijgt men:
langs de genoemde
assen voortplant, verkrijgt men:
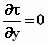
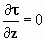
Uit deze vergelijkingen volgt dat τ
inderdaad een lineaire functie is:
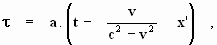
waarbij a een vooralsnog onbekende functie φ(v)
is en waarbij verder voor het gemak is aangenomen dat in het beginpunt van
het stelsel k de afspraak geldt: als τ = 0
dan is t = 0 .
Met behulp van dit resultaat verkrijgt men eenvoudig de
grootte van ξ , η en ζ als men
bedenkt dat het licht zich ook, gemeten in het stelsel-in-beweging, met de
snelheid c voortplant (zoals het principe van de constantheid
van de lichtsnelheid in combinatie met het relativiteitsprincipe vereist).
Voor een op het tijdstip τ = 0 in de richting van de
positieve ξ - as uitgezonden lichtstraal geldt dan:
ξ = c .τ
of
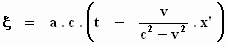 .
.
Nu heeft de lichtstraal echter ten opzichte van het beginpunt van het stelsel k , gemeten in het
stelsel-in-rust, een snelheid c – v , zodat geldt:
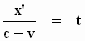
Als we deze waarde voor t in de
vergelijking voor ξ invullen, verkrijgen we:
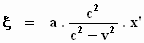
Door de lichtstralen te beschouwen die zich langs de
beide andere assen voortplanten, vinden we op een soortgelijke manier:
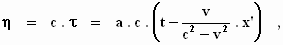
waarbij

dus
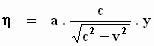
en op dezelfde manier:
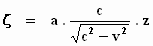
Als we voor x’ zijn waarde x – v
. t invullen, verkrijgen we:
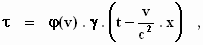
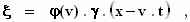
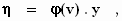
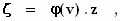
waarbij
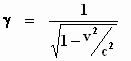
en waarbij φ nog steeds de vooralsnog
onbekende functie van v is. Legt men de beginpositie van het
stelsel-in-beweging en het nulpunt van τ niet vast, dan
moet bij de rechterzijde van ieder van deze vergelijkingen nog een
(integratie) constante worden opgeteld.
We moeten nu bewijzen dat iédere lichtstraal, gemeten in
het stelsel-in-beweging, zich met de snelheid c voortplant,
zoals dit, naar we hebben aangenomen, in het stelsel-in-rust
het geval is; want we moeten het bewijs nog leveren dat
het principe van de constantheid van de lichtsnelheid in overeenstemming is
met het relativiteitsprincipe.
Op het tijdstip t = τ = 0 wordt uit de
op dat tijdstip gemeenschappelijke oorsprong van de coördinaten van beide
stelsels een bolvormige lichtgolf uitgezonden, die zich in het stelsel K
met de snelheid c uitbreidt. Als (x, y, z) een
punt is dat net door de golf wordt bereikt, dan geldt
x 2 + y 2 + z 2 =
c 2 . t 2 .
Deze vergelijking transformeren we met behulp van onze
transformatieformules en we verkrijgen na een eenvoudige berekening:
ξ 2 + η 2 + ζ 2
= c 2 .τ 2 .
De beschouwde golf is dus ook in het stelsel-in-beweging
gezien een bolvormige golf die zich met de snelheid c
uitbreidt. Hiermee is aangetoond dat onze beide basisprincipes met elkaar te
verenigen zijn.
In de afgeleide transformatieformules treedt nog de
onbekende functie φ van v op welke we nu
gaan bepalen.
Hiertoe voeren we nog een derde coördinatenstelsel K*
in, met assen die evenwijdig zijn aan de assen van de beide andere stelsels,
en dat parallel ten opzichte de ξ-as van het stelsel k
een zodanige transformatiebeweging uitvoert, dat de oorsprong van het nieuwe
coördinatenstelsel met de snelheid – v langs de ξ-as
beweegt. Op het tijdstip t = 0 laten we de oorsprong van alle
drie de coördinatenstelsels samenvallen en we nemen aan dat op t = x
= y = z = 0 de tijd t* van het stelsel K* ook
gelijk is aan nul. We noemen x* , y* , z* de coördinaten,
gemeten in het stelsel K* , en we verkrijgen door
achtereenvolgens tweemaal onze transformatieformules toe te passen:
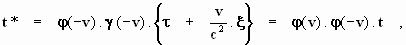



Aangezien de betrekkingen tussen x* , y* , z*
en x , y , z niet de tijd t bevatten, moeten de
stelsels K en K* samenvallen en hieruit is het duidelijk dat de transformatie van K
naar K* de identieke transformatie moet zijn. Daarom geldt:
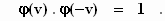
We vragen ons nu af wat de betekenis van φ(v)
is. We beschouwen het stuk van de η-as van het stelsel k
dat zich bevindt tussen ξ = 0, η = 0, ζ = 0 en ξ =
0, η =ℓ , ζ = 0 . Dit stuk van de η-as
is een ten opzichte van het stelsel K met een snelheid v
loodrecht ten opzichte van zijn eigen as bewegende staaf, waarvan de
uiteinden in K de volgende coördinaten bezitten:
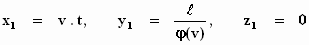
en
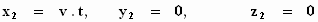 .
.
De lengte van de staaf, gemeten in K, is
dus ℓ /φ(v) ; waarmee de betekenis van de functie φ
duidelijk is. Uit symmetrieoverwegingen is het zonneklaar, dat de in het
stelsel-in-rust gemeten lengte van een staaf, die loodrecht ten opzichte van
zijn as beweegt, slechts van de snelheid, maar niet van de richting of van
de positieve of negatieve zin van de beweging, afhankelijk kan zijn. De
lengte van de bewegende staaf, gemeten in het stelsel-in-rust, verandert dus
niet als v door – v wordt verwisseld. Hieruit
volgt:
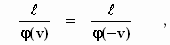
of
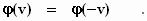
Uit deze en uit de eerder gevonden relatie volgt dat φ(v)
= 1 moet zijn, zodat de gevonden transformatieformules overgaan in:
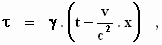
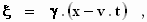
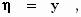
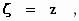
waarbij
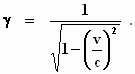
Terug
