II. Elektrodynamisch
gedeelte.
§ 6. De transformatie van de Maxwell–Hertz vergelijkingen voor de lege
ruimte. Over de aard van de bij een beweging in een magnetisch veld optredende
elektromotorische krachten.
We gaan uit van geldigheid van de Maxwell–Hertz vergelijkingen in de lege
ruimte voor het stelsel-in-rust K. Dan geldt:
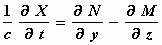 ;
; 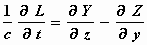
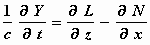 ;
;
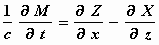
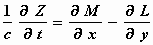 ;
; 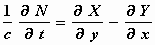
waarbij (X, Y, Z) de vector van de elektrische kracht en (L, M, N)
die van de magnetische kracht voorstelt.
Passen we op deze vergelijkingen de in § 3 afgeleide transformatieformules toe,
waarbij we de elektromagnetische gebeurtenissen op het daar ingevoerde, met een
snelheid v bewegende coördinatensysteem betrekken, dan verkrijgen we de
vergelijkingen:
|
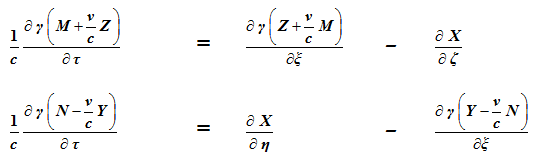
waarbij
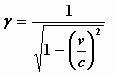
|
|
Het relativiteitsprincipe eist nu dat de Maxwell-Hertz vergelijkingen voor de
lege ruimte, als ze in het stelsel K geldig zijn, ook in het stelsel k
moeten gelden, hetgeen betekent dat voor de in het bewegende stelsel k
-
op grond van de ponderomotorische werking op een elektrisch geladen
voorwerp respectievelijk een magnetisch voorwerp - gedefinieerde
vectoren voor de elektrische kracht (X’, Y’, Z’) en de magnetische
kracht (L’, M’, N’) de volgende vergelijkingen in het
bewegende stelsel k moeten gelden:
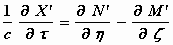 , ,
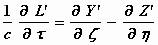 ,
,
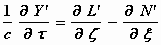 , ,
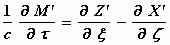 ,
,
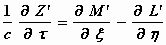 , ,
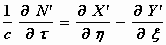 ,
,
|
|
Blijkbaar moeten nu de beide voor k gevonden stelsels vergelijkingen
precies hetzelfde uitdrukken, omdat beide stelsels vergelijkingen equivalent moeten zijn
aan de Maxwell–Hertz vergelijkingen voor het stelsel K. Aangezien de
stelsels vergelijkingen op de symbolen na die de vectoren voorstellen,
overeenstemmen, volgt daaruit dat de functies op overeenkomstige plaatsen in
beide stelsels vergelijkingen aan elkaar gelijk moeten zijn op een, voor alle
functies gemeenschappelijke factor ψ(v) na, die niet afhankelijk is
van ξ, η, ζ en τ , maar wel van de snelheid v
afhankelijk kan zijn. Er gelden dan de volgende betrekkingen:
X’ = ψ(v) X ,
L’ = ψ(v) L ,
Y’ = ψ(v) γ ( Y – 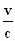 N
) , M’
= ψ(v) γ ( M + N
) , M’
= ψ(v) γ ( M + 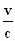 Z
) , Z
) ,
Z’ = ψ(v) γ ( Z + 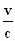 M
) , N’
= ψ(v) γ ( N – M
) , N’
= ψ(v) γ ( N – 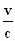 Y
). Y
).
Wanneer men nu in omgekeerde richting deze stelsels vergelijkingen opstelt,
wat in de eerste plaats kan door de net verkregen vergelijkingen op te lossen en
in de tweede plaats door op de vergelijkingen de inverse transformatie (van k
naar K ) toe te passen, die gekarakteriseerd wordt door de snelheid –v
, dan volgt daaruit, als men in gedachten houdt dat de verkregen stelsels
vergelijkingen identiek moeten zijn:
|
ψ( v ) . ψ( –v ) = 1 .
Verder volgt uit symmetrieoverwegingen 1)
ψ( v ) = ψ( –v ) ;
er geldt dus
ψ( v ) = 1 ,
en onze vergelijkingen krijgen dus de volgende vorm:
X’ = X ,
L’ = L ,
Y’ = γ ( Y – 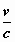 N
) , M’ = γ ( M + N
) , M’ = γ ( M + 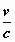 Z
) , Z
) ,
Z’ = γ ( Z + 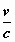 M
) , N’ = γ ( N – M
) , N’ = γ ( N – 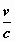 Y
) . Y
) .
|
|
Over de interpretatie van deze vergelijkingen merken we het volgende op: we
gaan uit van een puntvormige hoeveelheid elektriciteit, die in het
stelsel-in-rust K gemeten de grootte één heeft, dat wil zeggen dat deze
hoeveelheid elektriciteit in rust in K op een even grote hoeveelheid
elektriciteit op een afstand van 1 cm een kracht van 1 dyne uitoefent. Volgens
het relativiteitsprincipe heeft deze elektrische lading ook in het
stelsel-in-beweging gemeten de grootte "één". Als deze hoeveelheid
elektriciteit in rust is ten opzichte van het stelsel-in-rust , dan is per
definitie de vector (X, Y, Z) gelijk aan de kracht die op die hoeveelheid
elektriciteit werkt. Is de hoeveelheid elektriciteit daarentegen ten opzichte van het
stelsel-in-beweging in rust (of tenminste op het beschouwde ogenblik), dan is de
erop werkende kracht, in het stelsel-in-beweging gemeten, gelijk aan de
vector (X’, Y’ ,Z’ ). De drie linker vergelijkingen hierboven
kunnen derhalve op de volgende twee manieren in woorden worden uitgedrukt:
- Als een puntvormige, elektrische eenheidslading zich door een
elektromagnetisch veld verplaatst, dan werkt daar behalve een elektrische kracht ook een "elektromotorische kracht"
op, die, bij verwaarlozing van de termen die met tweede en hogere machten van v/c
worden vermenigvuldigd, gelijk is aan het door de lichtsnelheid gedeelde
vectorproduct van de bewegingssnelheid van de eenheidslading en de magnetische
kracht. (Oude omschrijving.)
- Als een puntvormige, elektrische eenheidslading zich door een
elektromagnetisch veld verplaatst, dan is de hierop werkende kracht gelijk
aan de ter plekke van de eenheidslading aanwezige elektrische kracht, welke
men verkrijgt door de transformatie van het veld naar een ten opzichte van
de elektrische eenheidslading rustend coördinatenstelsel. (Nieuwe
omschrijving.)
Een analoge redenering geldt voor de "magnetomotorische krachten".
Men ziet dat de elektromotorische kracht in de hier gepresenteerde theorie
slechts de rol van een hulpbegrip speelt, dat zijn invoering te danken heeft aan
het feit dat men vroeger niet heeft doorzien dat de elektrische en magnetische krachten
niet een onafhankelijke existentie bezitten, maar afhankelijk zijn van de
bewegingstoestand van het coördinatenstelsel
.
Verder is het duidelijk dat de in de inleiding genoemde asymmetrie verdwijnt die
opduikt bij de
beschouwing over de stromen die ontstaan als een magneet en een geleider zich
ten opzichte van elkaar verplaatsen . Ook de vraag naar de
"plaats" van de elektrodynamische en elektromotorische krachten (unipolaire
machines) heeft geen betekenis.
|
|