§ 7. Theorie over het beginsel van Doppler en over aberratie.
Op zeer grote afstand van de oorsprong in het coördinatenstelsel K bevindt zich
een (stilstaande) bron van elektromagnetische golven. De golven van
deze bron kunnen in de buurt van de genoemde oorsprong voldoende nauwkeurig door de volgende
vergelijkingen worden beschreven:
X = X0 sin Φ
; L = L0 sin
Φ
Y = Y0 sin Φ
; M = M0 sin
Φ
Z = Z0 sin Φ ; N = N0 sin
Φ
Φ = ω 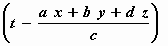
Hierin zijn (X0 , Y0 , Z0 ) en (L0
,
M0 , N0) de vectoren waarmee de amplitude van de golftrein
wordt aangegeven en a, b, d zijn de richtingscosinussen 1) van
de normaal op de golf.
We vragen ons af welke beschrijving een waarnemer van deze golven zal geven die
zich in een stelsel-in-beweging k in rust bevindt. Door de
in §6 gevonden transformatieformules voor de elektrische en magnetische
krachten en de in § 3 gevonden transformatieformules voor de coördinaten en de
tijd toe te passen, worden de volgende vergelijkingen verkregen:
X’ =
X0 sin Φ’
; L’ = L0 sin Φ’
Y’ = γ ( Y0 – 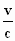 N0
) sin Φ’
; M’ = γ ( M0 +
N0
) sin Φ’
; M’ = γ ( M0 + 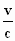 Z0
) sin Φ’
Z0
) sin Φ’
Z’ = γ ( Z0 + 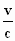 M0
) sin Φ’
; N’ = γ ( N0 –
M0
) sin Φ’
; N’ = γ ( N0 – 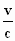 Y0
) sin Φ’
Y0
) sin Φ’
Φ’ = ω’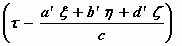 ,
,
waarbij het volgende geldt:
ω’ = ω γ 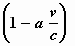
a’ = 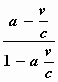
b’ = 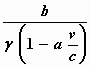
d’ = 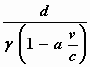
Uit de vergelijking voor ω’ volgt: Als een waarnemer in
beweging is ten opzichte van een oneindig ver weg gelegen lichtbron met de frequentie f
2) , zodanig dat zijn snelheid een hoek φ
vormt met de verbindingslijn "lichtbron
-waarnemer", gemeten in een coördinatenstelsel dat
in rust is ten opzichte van de lichtbron, dan is de door de waarnemer
waargenomen frequentie f ’ van het licht met de volgende
uitdrukking te vinden:
f ’ = f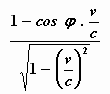
Dit is het Beginsel van Doppler voor
elektromagnetische golven.
Voor φ
= 0 neemt de
formule de volgende overzichtelijke vorm aan:
f ’ = f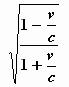
Men ziet — in strijd met de gebruikelijke opvatting — dat voor
v
= – ∞ de frequentie f = ∞
wordt 3)
.
Als men φ’ de hoek tussen de normaal
op de golf (richting van de lichtstraal) in het stelsel-in-beweging en de
bewegingsrichting 4) noemt, dan neemt de uitdrukking
voor a’ de volgende vorm aan:
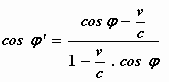
Deze vergelijking is de meest algemene uitdrukking voor de aberratiewet. Als φ
= π /2, dan neemt de vergelijking de volgende, eenvoudige
vorm aan:
cos φ’ = – 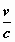 .
.
We moeten nu nog de amplitude van de golven zoals deze in het
stelsel-in-beweging voorkomen, bepalen. Noemt men achtereenvolgens A en A’
de amplitude van de elektrische of de magnetische kracht die gemeten is in het
stelsel-in-rust respectievelijk het stelsel-in-beweging, dan verkrijgt men:
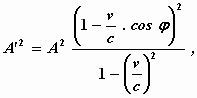
welke vergelijking voor φ = 0 overgaat in de eenvoudige
vorm:
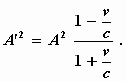
Uit de gevonden vergelijkingen volgt dat voor een waarnemer, die met de
snelheid c een lichtbron nadert, deze lichtbron oneindig intensief
moet lijken.
