3
De Belemmeringstheorie en de extra gravitatieversnelling
De versnelling die een voorwerp ondervindt, hangt direct samen met het
verloop van de tijdvertraging die in de buurt van de massa wordt ervaren. Om
exact te zijn: de versnelling is evenredig aan de gradiënt van de
tijdvertraging.
Wanneer
we –
zoals de Belemmeringstheorie
voorschrijft – een massa opvatten als een
belemmering die ons het zicht op het achterliggende universum belet, moeten we
van die belemmering de grootte bepalen. Die blijkt gelijk te zijn aan de ruimtehoek die de zwarte vlek
inneemt die rond de massa bestaat, vanuit de waarnemer gezien.
 |
Onder
de zwarte vlek verstaan we het gebied binnen de Einsteinring
rond een massa. Voor de Einsteinring geldt
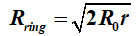meter. |
De ruimtehoek is dan
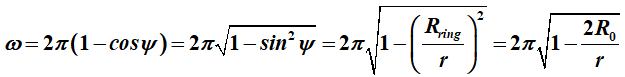sr. Hierin is r
de afstand waarop de massa zich bevindt, y
is de hoek waaronder de straal van de Einsteinring
wordt waargenomen en R0
is de straal van het zwarte gat waartoe de massa kan worden samengeperst
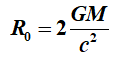meter.
Deze
ruimtehoek, in vergelijking tot de totale ruimtehoek die het universum
inneemt, kan - zoals eerder gezegd - gelijk worden gesteld
aan de tijdvertraging (TVT) op die plaats want
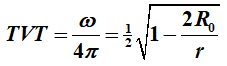sec/sec . Mits
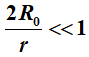, wordt dit
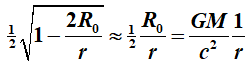sec/sec .
Dit is
de bekende uitdrukking van Einstein voor de tijdvertraging op de afstand r
van een massa.
Daaruit vinden we de gravitatieversnelling via de afgeleide naar r , dwz de gradiënt, en
vervolgens vermenigvuldigd met c2
:
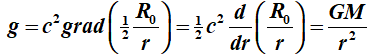m/sec2.
Als we
echter uitgaan van de exacte ruimtehoek wordt de versnelling:
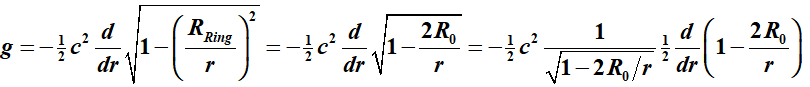
Met
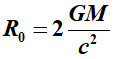verkrijgen we een nieuwe
zwaartekrachtformule:
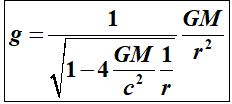m/s2.
|
Dit
is de verbeterde formule van Newton volgens de Belemmeringstheorie.
|
Voor
afstanden binnen het zonnestelsel - maar voldoende ver buiten de zon - mogen we
de formule benaderen met
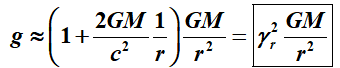m/s2.
Dit is een uiterst belangrijk resultaat van de Belemmeringstheorie omdat
voor het eerst na eeuwen de formule van Newton uit 1686 een verbetering
ondergaat. Er blijkt uit dat de gravitatieversnelling altijd iets groter is
dan met de formule van Newton wordt berekend.
|
De vraag is in
welke mate deze vernieuwde formule kan bijdragen aan het begrijpen van de
anomale versnellingen die de Pioneers en
de komeet Oumuamua volgens metingen ondergaan.
|
Als we
de formule uitwerken, vinden we
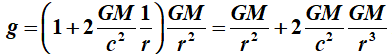m/s2.
De
eerste term
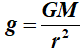herkennen we als de zwaartekrachtformule van Newton.
De
tweede term
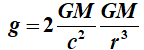is de extra
zwaartekracht versnelling.
We zien
dat de extra versnelling afneemt met de derde
macht van de afstand.
In de
zwaartekrachtwet van Newton is de afname van de versnelling kwadratisch.
Iedere bijdrage aan de versnelling die volgens metingen kwadratisch verloopt, zal daarom aan
de massa worden toegeschreven als er geen andere verklaring voor is.
Zo'n andere verklaring geldt bijvoorbeeld voor de tegenwerkende versnelling en
vertraging die de Pioneers kregen bij het naderen en het weer weggaan van de
zon door de "Outgassing" van de komeet vanwege de stralingsdruk
van de zon.
Een term die met de derde macht afneemt, springt er echter uit. Dat deze afwijking nooit eerder is
opgevallen, komt omdat de waarde ervan op de grens van het meetbare ligt:
ongeveer 1x10–10
m/s2 op de
afstand waarop de aarde zich bevindt. Dat is 1/100 van één miljardste
deel van de zwaartekrachtversnelling aan het aardoppervlak.
We
zullen onderzoeken of hiermee de afwijkingen in de baanbewegingen van de
Pioneers (§6)
en Oumuamua (§7–8)
te verklaren zijn.
Terug
