Naar
Inleiding
Naar Deel III
Naar Deel V
4
Effect van de werkelijke snelheid op de versnelling.
Als de snelheid van een voorwerp op zeer grote afstand van een grote
massa gelijk is aan v0
m/s dan is volgens Newton, wanneer het voorwerp in vrije val vanwege de
gravitatieversnelling naar de
massa beweegt, de snelheid op de afstand r
gelijk aan
m/s.
Volgens
§ 2 is de werkelijke
snelheid
m/sec.
Met de
uitdrukking voor v
wordt dat
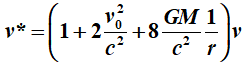m/s.
De
snelheid v*
wijkt nauwelijks af van de snelheid v
die met de traditionele theorie wordt berekend, want v02/c2
is van de orde 10–9 en de laatste term binnen de haakjes op 1 AE in de orde van 8x10–8.
De
laatste term levert echter wel waarden op voor de versnellingen die meetbaar zijn
.
We
vinden deze versnelling door te berekenen hoeveel de snelheid afneemt in 1 sec als het voorwerp zich radiëel van de zon verwijdert met de
snelheid v*
m/s. Dan heeft het voorwerp een afstand afgelegd van v* ≈ v meter.
De afname van de
snelheid in 1 sec vinden we met
We
krijgen met de uitdrukking voor v voor deze versnelling:
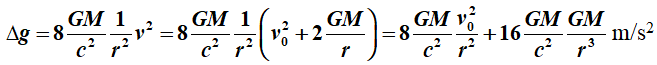
De
eerste term van de uitkomst neemt kwadratisch af met de afstand en zal dus in
de traditionele aanpak als een deel van de massa worden beschouwd omdat hij
aan de gravitatiewet van Newton voldoet. Hij treedt echter alleen op voor een
object dat in de verre ruimte een basissnelheid v0
heeft
en is afhankelijk van de grootte van die snelheid.
In de verre ruimte heeft de Pioneer 10 een snelheid van v0 =
11,2 km/sec.
Daarmee vinden we voor de eerste term
= 0,67x10–10 m/s2.
De tweede term is niet afhankelijk van de basissnelheid v0
en heeft een waarde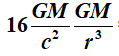 
=
9.36x10–10 m/sec2.
De
laatste term
m/sec2 is echter een 3de
machtsterm die onbekend is in de gevestigde theorie. Dit noemen wij de anomale
versnelling. Deze 3de machtsterm is ter hoogte van de aardbaan
zelfs groter dan de extra versnelling door de 2de machtsterm.
De
3de machtsterm kan alleen bij zeer nauwkeurige metingen aan het licht
komen.
Wanneer de snelheid een
hoek j
maakt met de gravitatieversnelling, krijgen we een versnelling van:
Deze
formule moeten we gebruiken voor de Pioneer 10 na zijn passage
langs Jupiter.
We
krijgen voor deze versnelling:
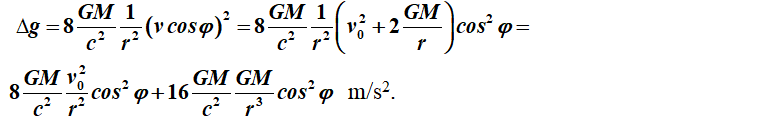
De
anomale versnelling krijgt nu de vorm:
m/s2.
Hieruit concluderen we - vanwege de term cos2j
- dat een object dat tangentiëel beweegt
ten opzichte van de heliocentrische afstand geen anomale versnelling vertoont.
Het is dan wel te begrijpen dat men uit de planeetbewegingen dit verschijnsel
niet heeft kunnen ontdekken. Daarom zijn kometen en objecten zoals Oumuamua en
de Pioneers bijzonder welkom om het bestaan van de extra versnellingen te
onderzoeken omdat zij in een snel tempo van heliocentrische afstand
veranderen.
Dat de
banen van de kometen niet al eerder de extra versnellingen aan het
licht hebben gebracht, kan een gevolg zijn van de flexibele correcties die via
het proces van "outgassing" kunnen worden gebruikt om elke
baanafwijking vlot te "verklaren".
Terug
Naar Deel V
