5
Relativistische massatoename
Zoals
uit de massa spectrometrie bekend is, neemt de 'massa' van een bewegend deeltje
toe met de snelheid. Er geldt voor de massa mv met de snelheid v dat deze gelijk is aan 
kg.
Dit wordt de relativistische
massa genoemd. Hierin is m de massa van het
deeltje als het in stilstand wordt gemeten en g
is de Lorentzfactor die hoort bij de
snelheid van het deeltje.
Wanneer
men met de massa de hoeveelheid materie bedoelt, is dit echter een dwaze
manier van spreken. De massa van het deeltje zou groter zijn geworden
voor een stilstaande waarnemer maar niet voor de waarnemer die met het deeltje
meebeweegt. Waar komt die extra materie vandaan? Het is duidelijk dat
dit in strijd is met de Grondwet van de natuurkunde (p.1).
Zo
sprekende, werkt men in de hand dat de wetenschap nog steeds zoekende is naar
hoe de zwaartekracht moet worden begrepen en wat onder massa moet worden
verstaan.
We moeten
onderscheid maken tussen de massa en de hoeveelheid
materie. Daarom hebben wij in de Belemmeringstheorie voor de massa van
een object een definitie ingevoerd waarbij niet de hoeveelheid materie
bepalend is voor de grootte van de massa maar de invloed die deze materiehoeveelheid uitoefent onder standaard
omstandigheden.
Dan kan men spreken over een toegenomen massa van een bewegend object zonder
dat de hoeveelheid materie is toegenomen. Het begrip massa hangt dan samen met
de eigenschap van een hoeveelheid materie om te belemmeren dat de straling van
achterliggende stralingsbronnen de waarnemer kan bereiken.
De zwarte vlek is dan de maat voor de hoeveelheid materie.
De
ruimtehoek van de zwarte vlek is gelijk aan
sr waarbij de straal van de
Einsteinring gelijk is aan
meter en waarin de straal R0 van het zwarte gat waartoe de massa M
kan instorten, gelijk is aan
meter.
De ruimtehoek die de Einsteinring van een hemellichaam met de snelheid v inneemt, zal
g
keer zo groot zijn als van
het stilstaande hemellichaam. Zo zal ook voor een waarnemer in een
ruimtevaartuig of op een komeet met een snelheid v
de ruimtehoek van de zon toenemen
omdat de zon ook beweegt ten
opzichte van deze objecten (zie verder het bewijs: T&C p. 127) . Dit zal de gravitatieversnelling van de zon op
de objecten versterken. Dit geldt zowel bij het naderen als het wegvliegen van
de zon.
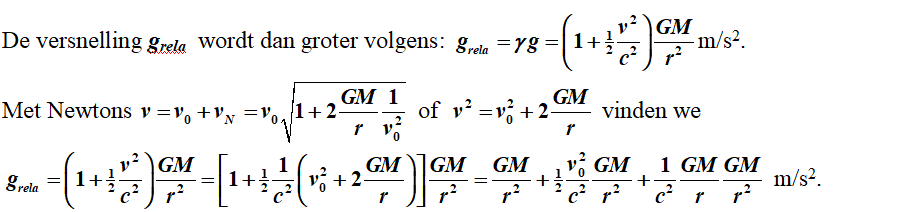
We herkennen de eerste term als de bekende gravitatiewet
van Newton, de tweede term als een kwadratisch afnemende term die als onderdeel
van de massa kan worden beschouwd en de laatste term
m/sec2 als een extra
versnelling die als 3de machtsterm van de afstand r
afwijkt van de gravitatiewet van
Newton.
Ook deze toename van de zwaartekrachtversnelling maakt, evenals de extra
zwaartekracht versnelling volgens de Belemmeringstheorie zoals beschreven
in §3, al sinds
lang deel uit van de traditionele theorie en wordt in de berekeningen
weggemoffeld door aan te nemen dat de ruimte gekromd is. We zullen verder in
het kader van het onderzoek naar de baanbewegingen van de Pioneers en Oumuamua
geen aandacht aan de hier genoemde toename besteden.
