|
§10 Toepassing: massa hangt af van de snelheid.
Naar Uitleg E=mc2
Naar Uitleg §9 Elektrische stromen
Naar Uitleg Inhoud
Naar Vertaling §10 Massa en versnelling
Naar Centrale Hal
In dit voorbeeld bespreekt Einstein de beweging van een geladen deeltje met
een lading ε en een massa m
in een elektrisch veld E.
Hij zit hier al heel dicht tegen de beroemde
formule E = m.c2 aan.
Hij gaat uit van een "langzaam versneld elektron". Deze voorzorg
moet hij nemen om de elektromagnetische straling, die een snel versneld geladen
deeltje uitzendt, te mogen verwaarlozen. Uit de theorie van Lorentz (Versuch
§30–35), gebaseerd op de theorie van Maxwell (A treatise, ) blijkt
dat de uitgezonden straling evenredig is met de versnelling van een geladen
deeltje.
De term "elektron" was toen enige jaren in gebruik voor de
ladingdragers van de elektriciteit, maar men wist nog niet dat een elektron een
vaste, minimale hoeveelheid lading bij zich draagt. Evenmin wist men met
zekerheid of het elektron een hoeveelheid "gewone" zware massa bezat
(zogenaamde pondorabele massa) of dat het geheel uit elektromagnetisme was
opgebouwd en hoe groot de "elektromagnetische massa" was.
Wetenschappers uit die tijd probeerden met grote inzet en verfijnde theorieën
te achterhalen voor welk deel de massa van geladen deeltjes uit zware massa en
voor welk deel het uit elektromagnetische massa bestond. Max Abraham had kort
daarvoor "aangetoond" dat de elektronen die bij radioactiviteit
vrijkomen en de elektronen die optreden bij kathodestralen geen zware massa
bezaten, doch uitsluitend elektromagnetische massa met zich meevoerden.
Men had verder berekend dat de elektromagnetische massa door zijn
"wisselwerking" met de ether groter zou worden als de snelheid toenam,
voor gewone massa zou dat niet gelden. Experimenteel onderzoek werd vooral
gedaan door W.Kaufmann, die zijn resultaten liever niet met de theorie van
Einstein in overeenstemming zag (zie W.Kaufmann: Konstitution de Elektrons;
Analen der Physik IV p. 487– 640).
Het was een verwarrende tijd.
De kracht op een elektron en dus ook op het "langzaam versnelde
elektron" is ε.E . De drie
richtingscomponenten van de kracht zijn ε.X
; ε.Y en ε.Z.
Vanuit rust is de snelheid in het begin gering (waarbij de beweging kan worden
benaderd met de wet van Newton: massa x versnelling = kracht) maar op zeker
moment is de snelheid v zodanig groot dat de benadering niet meer opgaat.
Immers, als de kracht hetzelfde blijft, moet de versnelling afnemen omdat de
snelheid nooit groter kan worden dan de lichtsnelheid.
We moeten dan overschakelen op de formules zoals ze gelden voor een
stelsel-in-beweging met de snelheid v. Dan veranderen de coördinaten x,
y, z en t in ξ, η, ζ en
τ (zie fig. 1001) en de
componenten van het elektrische veld X, Y en Z in X', Y' en
Z'.
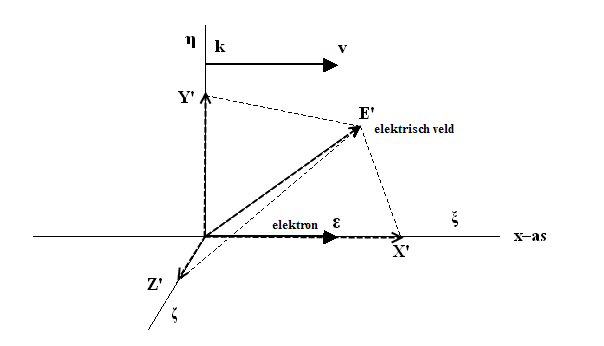
Figuur 1001 Een versneld elektron in een elektrisch veld
Omdat de snelheid toeneemt, gelden de formules voor ξ,
η, ζ, τ en X',
Y' en Z' slechts gedurende korte tijd, namelijk zolang de snelheid
nog weinig veranderd is ten opzichte van de waarde v.
Daarna moet je eigenlijk de formules aanpassen met een nieuwe waarde voor de
snelheid van het stelsel-in-beweging, maar zover hoeven we niet te gaan omdat we
de snelheid niet willen uitrekenen, maar een formule willen opstellen. Als
volgt:
De lading ε blijft constant
omdat de lading een invariante grootheid is (zie §9). Over de massa m
laten we ons voorlopig niet uit. De bewegingsvergelijkingen (massa x versnelling
= kracht) voor de x–, y– en z–richting in het
stelsel-in-beweging zijn:
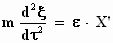
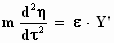
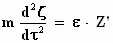
Even ter herinnering: de eerste afgeleide van de plaats naar de tijd is
de snelheid en de tweede afgeleide, die we hier zien, is de versnelling
We passen het beproefde recept toe: transformeren! De transformatieformules
zijn:
|
Naar bewegende stelsel
voor tijd en plaats |
naar stilstaand stelsel
voor tijd en plaats |
naar bewegende stelsel
voor het elektrisch veld |
|
τ = γ . (t – 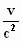 .x) .x) |
t = γ. (τ + 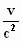 .
ξ) .
ξ) |
|
|
ξ = γ . (x – v.t) |
x = γ. (ξ + v.
τ) |
X' = X |
|
η = y |
y = η |
Y' = γ . (Y – 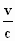 .N) .N) |
|
ζ = z |
z = ζ |
Z' = γ . ( Z + 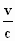 .M) .M) |
We bekijken de bewegingsvergelijking voor de x–richting.
Terwijl het stelsel-in-beweging k met de snelheid v voortvliegt,
krijgt het elektron in dat stelsel een snelheid 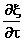 die ongelijk is aan 0 . De snelheid van het deeltje zal vanuit het
stelsel-in-rust gezien dan ook niet meer gelijk aan v zijn, dus
die ongelijk is aan 0 . De snelheid van het deeltje zal vanuit het
stelsel-in-rust gezien dan ook niet meer gelijk aan v zijn, dus 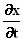 –
v ≠ 0. –
v ≠ 0.
Ik wil je hier op een eigenaardigheid wijzen. Bij een
"normale" functie, mag je meestal stellen
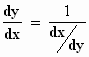 ,
of ,
of 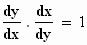
Bijvoorbeeld als y = x2, dan is 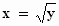 en voor de afgeleiden geldt dan:
en voor de afgeleiden geldt dan:
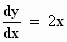 en
en
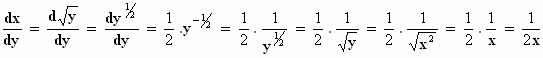
Je ziet: er geldt voorbeeldig
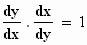 (behalve als x=0).
(behalve als x=0).
Dat nu geldt in het algemeen niét als je een functie differentieert die van
meer dan één variabele afhangt, zoals bijvoorbeeld ξ
, die van x en t afhangt:
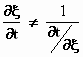
Je moet dan netjes gebruik maken van de transformatieformules voor ξ,
τ en x en t
ξ = γ. (x – v.t)
en
x = γ. (ξ + v. τ)
τ = γ. ( t – 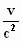 .x)
en
t = γ. (τ + .x)
en
t = γ. (τ + 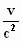 .
ξ) .
ξ)
De bijbehorende afgeleiden zijn:
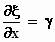 en
en
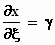
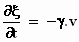 en
en
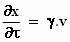
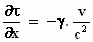 en
en
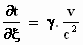
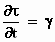 en
en
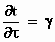
Hier zullen we af en toe gebruik van maken.
Omdat
η = y ,
y = η , ζ = z ,
z = ζ ,
dus niet van twee variabelen afhankelijk zijn,
levert
differentiatie naar deze variabelen geen extra problemen
op.
Met dit in gedachten zullen we uitzoeken hoe Einstein van de formule 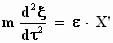 op de formule
op de formule 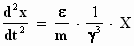 komt. komt.
Eerst transformeren we de uitdrukking 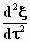 .
We maken zoveel mogelijk gebruik van de afgeleiden uit de tabel hierboven: .
We maken zoveel mogelijk gebruik van de afgeleiden uit de tabel hierboven:
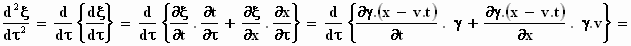
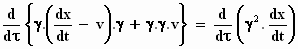
Dit was een eerste stap, die kwam mooi uit want de differentiatie naar x viel
weg.
We moeten dit nog een keer herhalen:
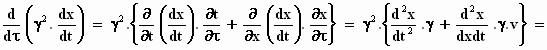
Het is lastig, even geduld, we zijn er bijna!
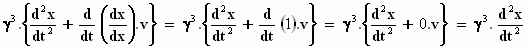
Bedenk verder dat X' = X en het zal duidelijk zijn hoe Einstein
van 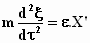 op
op 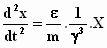 komt.
komt.
Het is belangrijk te zien dat de massa, noch de elektrische lading een rol
spelen in deze transformatie.
 |
Misschien welt onstuitbaar de vraag in je op: "Hoe kan dat nou, de massa
m is toch geen invariante grootheid zoals ε?
De massa is toch afhankelijk van de snelheid, dus moet je m toch ook
transformeren!?"
Dan wil ik je wijzen op het patroon dat zichtbaar wordt in de manier
waarop de transformatieformules voor verschillende grootheden worden gevonden.
We zoeken een vergelijking waarin de transformatieformules voor alle grootheden
op één na bekend zijn. We transformeren de vergelijking en uit het resultaat
halen we de onbekende transformatieformule voor de grootheid waar we naar opzoek waren. Het lijkt op het oplossen van een vergelijking met één onbekende! |
De transformaties voor de y– en de z–richting zijn wat
eenvoudiger. Probeer ze maar.
Zo verkrijgen we de volgende versnellingen van het "elektron" voor
de drie richtingen:
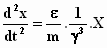
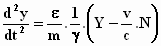
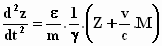
Einstein bespreekt vervolgens de massa van het elektron op de manier, zoals
hij met enige terughoudendheid stelt, die in die tijd gebruikelijk was. Men
onderscheidde de "longitudinale" en de "transversale" massa.
De eerste is de trage massa die zich voordoet en bepalend is voor de
versnelling, als een deeltje een kracht
ondervindt in de x–richting en de transversale massa is de trage massa
die zich voordoet als een deeltje een kracht ondervindt in een richting
die loodrecht staat op de x–richting.
 | Het was toentertijd al uit experimenten bekend dat
de
trage massa bij toenemende snelheid groter wordt (dus: die kennis was
ouder dan de relativiteitstheorie!). |
Hierboven staan de versnellingen. De bijbehorende krachten zijn:
voor de x–richting :
ε . X
voor de y–richting :
ε . γ
.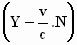
voor de z–richting :
ε . γ
.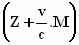 . .
Einstein: "Deze krachten zouden met een veerbalans in het stelsel-in-beweging kunnen
worden gemeten".
Dat is nou zo schattig van Einstein, zit je
midden in de relativiteitstheorie en dan komt hij met een veerbalans! Zullen we
de Maagdenburger halve bollen er maar buiten laten!
Het zet ons echter wel met beide benen op de grond: de kracht in het
stelsel-in-beweging kan gewoon worden gemeten. Als daar 10 newton wordt gemeten
en men seint dat over, dan verandert dat onderweg niet in 12 newton, het blijft
gewoon 10 newton!
Uit een vergelijking van de drie krachten en de drie versnellingen zoals ze
net zijn opgesomd, volgt voor de massa:
in de x–richting (longitudinale massa):
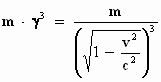
in de y– en de z–richting (transversale massa):
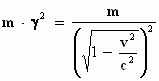
 |
Het wordt steeds bonter, niet alleen dat de massa geen invariante grootheid
is, de massa is in de ene richting ook nog eens een andere dan in de andere
richting. Je verwacht eigenlijk dat de massa alleen in de x–richting
beïnvloed wordt, want dat hebben we ook gezien bij de lengte. De
transformatieformules voor de y– en de z–richting zijn immers : y = η
en z = ζ dus verwacht je ongewijzigde bewegingsvergelijkingen
in die richtingen. Maar dan heb je buiten de "tijd" gerekend: in het
stelsel-in-beweging gaat alles trager, ook de versnelling in
"transversale" richting, dus moet de grotere, trage massa daar
de"oorzaak" van zijn. |
Omdat γ groter dan 1
is, neemt de massa toe met de snelheid, in de x-richting met de derde
macht van γ en in de richting
loodrecht daarop met het kwadraat van γ
.
In §5 hebben we gezien dat de snelheid
moeizamer toeneemt als je twee snelheden bij elkaar optelt waarvan er één al
dicht bij de lichtsnelheid is. Dat klopt goed met dit verhaal over de toenemende
massa, het effect van de kracht op de snelheid wordt steeds minder naarmate de
snelheid groter wordt. Als v de lichtsnelheid nadert, gaat de massa naar
oneindig!
(Omdat de term onder het wortelteken 0 wordt en delen door 0
, nou dan weet je het wel…….).
Dan wordt het langzamerhand onmogelijk nog
iets aan de snelheid toe te voegen.
Het is opmerkelijk dat de formule voor de massa m voor een massa met een
snelheid v , zoals deze in alle schoolboeken staat:
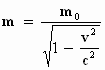 helemaal niet uit het verhaal van Einstein lijkt te volgen. (Hierin is m0
de "rustmassa", dat is de massa bij de snelheid v = 0. Zijn we altijd
voor de gek gehouden? Zie kader Max Planck.)
helemaal niet uit het verhaal van Einstein lijkt te volgen. (Hierin is m0
de "rustmassa", dat is de massa bij de snelheid v = 0. Zijn we altijd
voor de gek gehouden? Zie kader Max Planck.)
Het is een vervelende gedachte dat de massa van een voorwerp afhankelijk is
van de richting waarin het wordt versneld. Einstein vond het kennelijk ook een
weinig fraaie theorie met zijn transversale massa en longitudinale
massa, zoals blijkt uit zijn tussenzin "…,waarbij we de
gebruikelijke beschouwingswijze volgen… ". Het was echter de gangbare
manier om er tegenaan te kijken. Hij maande al tot voorzichtigheid omdat het
resultaat afhankelijk is van de definitie van de kracht en de versnelling, maar
hij had kennelijk geen zin of tijd dat allemaal nog eerst uit te zoeken..
Max Planck 1) begreep de hint en ging direct op zoek naar de
juiste definities voor de versnelling en de kracht om tot een eenduidige massa
te komen. De oplossing van het probleem lag niet voor de hand. Pas driekwart
jaar na Einsteins artikel publiceert Planck zijn aanvulling. Hij laat via enige
gruwelijk ingewikkelde berekeningen zien dat als je de snelheid van het elektron
v niet langs de x–as, maar in een willekeurige richting, met componenten (vx,
vy, vz), laat verlopen, de relatie tussen massa,
versnelling en kracht (Fx, Fy, Fz) voor het
bewegende elektron de volgende vormen aanneemt, de bewegingsvergelijkingen:
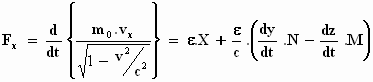
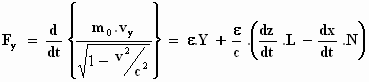
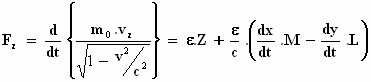
Zo geschreven behoudt de formule zijn vorm in het stelsel-in-beweging en
voldoet aan het relativiteitsprincipe.
Het product m .v (massa maal snelheid) wordt de impuls van een bewegend
voorwerp genoemd. Volgens Max Planck is de kracht niet gelijk aan de massa maal
de verandering van de snelheid, maar de kracht is de verandering van het product
van massa en snelheid. De massa zelf is eveneens afhankelijk van de snelheid,
de "relativistische massa" of "impulsmassa": 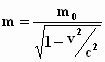 ,
waardoor je een andere uitkomst krijgt. ,
waardoor je een andere uitkomst krijgt.
De massa is op deze manier geschreven, niet afhankelijk van de richting.
De formules van Einstein klopten voor een snelheid langs de x–as. Plancks
formules gelden ook voor de transversale richtingen en je ziet: het voorwerp
heeft maar één massa.
Alleen al met het narekenen van het verhaal van Planck is een normaal mens
een week bezig, want het is een gedoe met coördinatentransformaties en
draaiingen van assenstelsels waar je tureluurs van wordt. Hoe verzon hij het.
Daarom: "Driewerf hoezee voor Planck!"
1) Max Planck: Das Prinzip der Relativiteit
und die Grundgleichungen der Mechanik; VhDPG band 8 1906 p.136-141. Duits
natuurkundige 1858-1947 Geboren in Kiel. Van 1889 tot 1928 was hij
hoogleraar theoretische natuurkunde in Berlijn. Samen met Einstein
grondlegger van de kwantumtheorie. Een moedig man in zijn strijd om de
Duitse wetenschap te behoeden voor een teloorgang gedurende het tijdperk van
het nationaal socialisme.
Terug
Verder merkt Einstein op dat de formules voor de massa, afgeleid voor een
geladen deeltje, ook gelden voor zware massa’s zonder elektrische lading,
omdat er altijd een geladen deeltje van kan worden gemaakt door er enige lading
aan toe te voegen. De versnelling die een massa krijgt als reactie op een kracht
wordt bepaald door zijn trage massa. Daar gelden die formules voor. Of die trage
massa nu is opgebouwd uit zware massa en "elektromagnetische massa" of
uitsluitend uit "elektromagnetische massa", dat maakt voor de
afgeleide formules niet uit.
De volgende, in die tijd gebruikelijke stap is het bepalen van de kinetische
energie van het elektron als het een snelheid v* heeft bereikt. Daar
werden toentertijd lange en ingewikkelde artikelen 2) over
geschreven. De behandeling hiervan door Einstein is kort en helder.
2) Max Abraham: "Prinzipien der Dynamik des
Elektrons"; Annalen der Physik , 10, 1903, p. 107 . In dit artikel doet
Abraham een bijna wanhopige poging de energie van het elektron te bepalen. Hoe
ontnuchterend moet het artikel van Einstein voor hem zijn geweest.
Ga uit van een elektron met een lading ε
en een veldsterkte X die langs de x–as is gericht. De kracht op
het elektron is dan ε.X. De
arbeid die het veld op het elektron verricht als dit zich verplaatst over een
afstand dx is gelijk aan ε.E.dx.
Je
vindt de arbeid W die over een bepaalde afstand door het veld op het
elektron wordt verricht eenvoudig met de integraal:
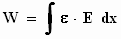
De arbeid die het veld op het elektron heeft verricht, is gelijk aan de
kinetische energie die het elektron heeft verkregen.
Omdat we de arbeid willen uitdrukken in de snelheid van v = 0 tot de
eindsnelheid v* zullen we de integraal moeten herschrijven met de
snelheid v als variabele.
Zoals we net hebben gezien is de bewegingsvergelijking van het elektron :
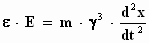
Hierin is de versnelling 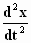 gelijk aan de verandering van de snelheid
gelijk aan de verandering van de snelheid 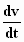 . .
We vullen onder de integraal de uitdrukking m . γ3
.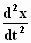 in voor ε
. E en vervolgens vervangen we in voor ε
. E en vervolgens vervangen we 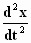 door
door 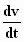 : :
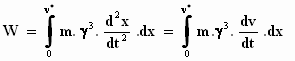
We lopen hier tegen het probleem op dat we van variabele moeten wisselen. We
hebben de variabele x en we willen de variabele v. We hebben al
een stapje in die richting gezet: van 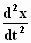 hebben we
hebben we 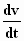 gemaakt. Zonder
al te diep op de wiskundige randvoorwaarden in te gaan, kunnen we stellen dat
een afstandje dx wordt afgelegd bij een snelheid v in een tijd dt
zodat dx = v.dt. Als we dit gebruiken, krijgen we: gemaakt. Zonder
al te diep op de wiskundige randvoorwaarden in te gaan, kunnen we stellen dat
een afstandje dx wordt afgelegd bij een snelheid v in een tijd dt
zodat dx = v.dt. Als we dit gebruiken, krijgen we:
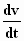 . dx = . dx = 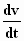 .
v. dt = v . dv. .
v. dt = v . dv.
De twee dt’s hebben gewoon tegen elkaar weggestreept! Nu krijgen we
een integraal die we aankunnen:
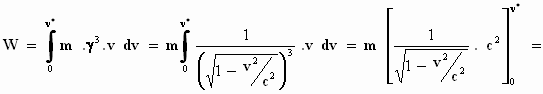
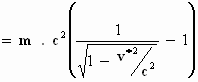
Het zal niet voor iedereen duidelijk zijn hoe we aan de primitieve functie 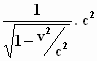 zijn gekomen. Daar valt weinig aan te doen. Het vinden van een primitieve
functie is een kwestie van proberen. Hoe vaker je het doet, hoe sneller je de
oplossing vindt. Het enige wat de beginner altijd moet doen, is aantonen dat de
veronderstelde primitieve functie dat ook daadwerkelijk is. Dat doe je door hem
te differentiëren en dan moet je de functie krijgen waar je de integraal over
hebt genomen. Dat laten we zien:
zijn gekomen. Daar valt weinig aan te doen. Het vinden van een primitieve
functie is een kwestie van proberen. Hoe vaker je het doet, hoe sneller je de
oplossing vindt. Het enige wat de beginner altijd moet doen, is aantonen dat de
veronderstelde primitieve functie dat ook daadwerkelijk is. Dat doe je door hem
te differentiëren en dan moet je de functie krijgen waar je de integraal over
hebt genomen. Dat laten we zien:
We integreerden over de snelheid v dus we moeten de primitieve functie
ook differentiëren naar v. We maken gebruik van de kettingregel (zie §3
blz 20) en het is handig om
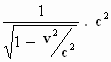 te schrijven als
te schrijven als 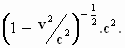
Dan krijgen we het volgende:
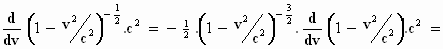
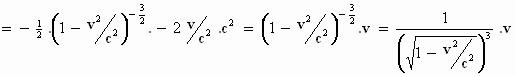
De laatste uitkomst is de uitdrukking die onder het integraalteken stond, dus de
veronderstelde primitieve functie is de juiste functie.
Omdat de eerder gevonden uitkomst voor elke waarde v* geldt, mogen we v*
vervangen door de willekeurige snelheid v. De uitkomst van de integraal wordt dus:
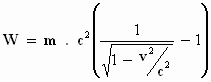
Dat is wel wat anders dan de vertrouwde Ekinetisch = ½ m v2
. Het heeft er echter wel veel mee te maken. Let maar op:
Om te beginnen is 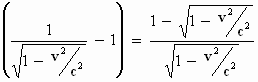
Als we nu terugkijken naar Uitleg §4 blz.10 dan zien we daar de
volgende benadering staan
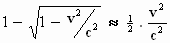
Dus
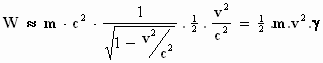
Voor snelheden die klein zijn ten opzichte van de lichtsnelheid is g
bij benadering gelijk aan 1, zodat W = ½ m v2. De energie Ekinetisch = ½ m v2 is dus een
benadering voor de werkelijke energie.
Het is overigens ongelofelijk hoe dicht Einstein hier met de formule
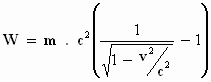
al bij de beroemde formule E = m. c2 zit. Die formule komt
in Uitleg E=mc2 aan de orde. Maar Einstein zag het
hier nog niet!
Onnodig op te merken dat als de snelheid v de lichtsnelheid c
nadert, de kinetische energie naar een oneindig grote waarde groeit.
Nogmaals benadrukt Einstein dat snelheden boven de lichtsnelheid niet kunnen
bestaan.
Niet ten onrechte, in de artikelen uit zijn tijd werd nog zonder blikken
of blozen gesproken over het bereiken van de lichtsnelheid. Zie
bijvoorbeeld Max Abraham "Zur Theorie der Strahlung und des
Strahlungsdruckes" Annalen der Physik, 14, 1904: p.287.
Het resultaat dat berekend is met een elektrische kracht moet ook voor een
gewone massa gelden, stelt Einstein nogmaals, want je kan een gewone massa van
een elektrische lading voorzien en weer hetzelfde verhaal houden. Het soort
massa, trage massa of "elektromagnetische massa" speelt geen rol in de
beschouwing.
Tot slot suggereert Einstein een drietal experimenten om de juistheid van de
bewegingsvergelijkingen van blz. 5 van deze paragraaf na te gaan.
Ten eerste:
Als de elektrische veldsterkte Y gelijk is aan 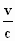 .
N , waarbij N de magnetische veldsterkte in de z–richting
is, dan is .
N , waarbij N de magnetische veldsterkte in de z–richting
is, dan is 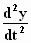 gelijk aan nul. Als er verder geen andere componenten van het elektrisch
veld of het magnetisch veld aanwezig zijn, zal, indien Y =
gelijk aan nul. Als er verder geen andere componenten van het elektrisch
veld of het magnetisch veld aanwezig zijn, zal, indien Y = 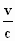 .
N het langs de x–as bewegende elektron een rechte lijn beschrijven,
terwijl voor zijn snelheid dan geldt: .
N het langs de x–as bewegende elektron een rechte lijn beschrijven,
terwijl voor zijn snelheid dan geldt: 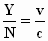 .
Op die manier is de snelheid eenvoudig te bepalen uit de verhouding van de
elektrische en de magnetische veldsterkte. De snelheid kan op onafhankelijke
wijze met behulp van snel oscillerende elektrische en magnetische velden worden
gemeten, stelt Einstein, zodat daarmee de bewegingsvergelijking kan worden
getoetst 3) .
Op die manier is de snelheid eenvoudig te bepalen uit de verhouding van de
elektrische en de magnetische veldsterkte. De snelheid kan op onafhankelijke
wijze met behulp van snel oscillerende elektrische en magnetische velden worden
gemeten, stelt Einstein, zodat daarmee de bewegingsvergelijking kan worden
getoetst 3)
3) Tot op heden heeft uw gids geen duidelijkheid
verkregen over de aard van de meetmethode om met wisselende velden de snelheid
van een elektron te bepalen, noch over de vraag of de door Einstein
gesuggereerde experimenten ooit zijn uitgevoerd.
Ten tweede:
Als je een elektron een elektrisch potentiaalverschil P (dat is een
spanningsverschil in bijvoorbeeld: volt) laat doorlopen, moet de snelheid
voldoen aan de vergelijking:
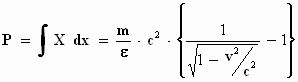 . .
Deze vergelijking hangt direct samen met de arbeid W die het veld op
het elektron heeft verricht om hem die snelheid te geven (zie blz. 7).
Het verlies aan potentiële energie Δ
ε . P van het elektron in het elektrisch veld moet gelijk zijn
aan de arbeid die het veld op het elektron heeft verricht, en dit is weer gelijk
aan de kinetische energie die het elektron heeft verkregen. Op deze wijze kan
aan een elektron een gewenste snelheid worden gegeven, die weer op
onafhankelijke wijze kan worden gecontroleerd.
Ten derde:
Als loodrecht op de snelheid in de x–richting van het elektron een
magnetisch veld N in de z–richting wordt aangebracht, als enige
afbuigende kracht, dan ondervindt het elektron een afbuiging in de y–richting
(zie bewegingsvergelijkingen op blz.3).
De versnelling wordt dan:
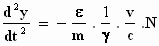
Het bijzondere daarvan is dat het elektron in het XY–vlak blijft
bewegen, zodat de kracht die van N uitgaat loodrecht op de snelheid
blijft werken. (de Lorentzkracht) en even groot blijft. De grootte van de
snelheid verandert daardoor niet, maar wel de richting. Het elektron gaat een
cirkel beschrijven. "Iedereen" weet dat de middelpuntzoekende kracht
die een deeltje met massa m en snelheid v in een cirkelbaan met
een straal R houdt, gelijk is aan: 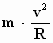 . .
De bijbehorende versnelling is dan: 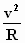 .
Stel beide uitdrukkingen voor de versnelling aan elkaar gelijk: .
Stel beide uitdrukkingen voor de versnelling aan elkaar gelijk:
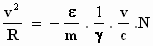
Hieruit volgt
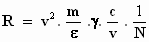
Hier geeft Einstein de volgende "mooie" vorm aan:
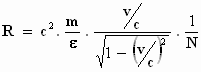
In deze vorm kan je de snelheidsverhouding 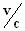 mooi gebruiken die uit zijn eerste experiment volgt.
mooi gebruiken die uit zijn eerste experiment volgt.
Met deze drie experimenten gaf Einstein nog wat huiswerk mee aan zijn
tijdgenoten.
Na nog enige woorden van dank aan zijn goede vriend Michele Besso besluit Einstein het artikel.
Einde
Opmerking:
Nog mijn felicitaties aan allen die met zoveel uithoudingsvermogen en met
zoveel inzet tot hier zijn gekomen. Je hebt de echte natuurkunde leren kennen,
ik bedoel, je hebt leren denken over de filosofische kant van de natuurkunde, je
hebt begrepen waar de werkelijke problemen liggen voor de wetenschap. Deze
natuurkunde heeft weinig met techniek te maken, maar alles met hoe de wereld is
opgebouwd.
Wie samen met mij deze cultuurschat heeft verkend en alle schitterende
gedachtegangen heeft gevolgd, zal, nu we bij het einde zijn gekomen, overvallen
kunnen worden door een treurig stemmend gevoel van nostalgie. Het is een beetje
alsof Einstein ons in de steek laat.
Maar!
Wat hoor ik nu?
Einstein geeft een toegift!
E = m . c2 !
Terug
|