|
div E = ρ
div B = 0 rot E =  rot B =
rot B = 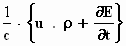
In de eerste duikt nu de lading op (als ladingsdichtheid ρ
) en in de laatste staat de stroomsterkte : de ladingsdichtheid ρ
maal de snelheid u waarmee die lading zich verplaatst. De betekenis van
de notaties div en rot hebben we in Uitleg §6 Maxwell
blz. 3 en verder al toegelicht. Voor de eerste formule geldt nu:

Eigenlijk luidt de formule div E = 4 πρ
, maar Einstein vond die 4π kennelijk wat ongemakkelijk en definieert
gewoon: ρ is de 4π-voudige ladingsdichtheid. Dat mag.
In de tijd dat Einstein zijn artikel schreef, stond de aard van het
verschijnsel elektriciteit nog niet duidelijk vast. De wetenschappers waren nog
volop bezig de theorie van Lorentz na te pluizen. Daarin stelt deze dat we ons
de elektriciteit moeten voorstellen als gebonden aan kleine massadeeltjes. Hij
noemde ze eerst ionen , naderhand elektronen.
De basis voor deze theorie werd gevormd door de vergelijkingen van Maxwell en
er is Einstein kennelijk veel aan gelegen om de elektronentheorie van Lorentz
eveneens onder het relativiteitsprincipe te laten vallen.
Ter herinnering: daarmee wordt bedoeld dat een waarnemer in een
stelsel-in-beweging de verschijnselen met dezelfde natuurkunde wetten moet
beschrijven als de waarnemer in het stelsel-in-rust.
Nog niet iedereen was overtuigd van de theorie van Lorentz en daarom was het
van belang dat Einstein die theorie betrok in zijn illustraties van het
relativiteitsprincipe.
Hoe toont Einstein aan dat de Maxwellvergelijkingen voldoen aan het
relativiteitsprincipe?
Het is heel eenvoudig. Je neemt de Maxwellvergelijkingen zoals ze gelden in
het stelsel-in-rust. Einstein schrijft ze voor de x–component, de y–component
en de z–component uit en vervolgens transformeer je ze met de formules
van §3 en §6. We hebben dat eerder gedaan (§6). Als de
getransformeerde vergelijkingen in wezen weer dezelfde vorm verkrijgen, voldoen
ze aan het relativiteitsprincipe.
Daar begin je opgewekt aan, het is niet moeilijk, maar je vergist je zo
gemakkelijk (en dus zo vaak!) dat je vele avonden verder bent voor de
transformatie correct is voltrokken. Je gaat zelfs even twijfelen aan Einstein!
Dat mag, Einstein is God niet, maar de twijfel aan Einstein wat deze theorie
betreft, is tot nu toe altijd ten onrechte gebleken.
Om goed beslagen ten ijs te komen, zetten we eerst alle transformatieformules
nog eens bijeen. Voor de coördinatentransformatie heen, maar ook terug.
De coördinatentransformaties zijn:
ξ = γ. (x – v.t)
maar ook
x = γ. (ξ + v.τ)
η = y
en
y = η
ζ = z
en
z = ζ
τ = γ. (t – 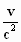 .
x)
en
t = γ . (t + .
x)
en
t = γ . (t +  .
ξ) .
ξ)
waarbij
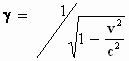
Voor de transformaties van de componenten van het elektrische veld in een
ruimte zonder ladingen hebben
we in §6 gevonden :
X' = X
Y' = γ. (Y – 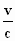 .
N) .
N)
Z' = γ. (Z +  .
M) .
M)
En voor de getransformeerde componenten van het magnetische veld in een
ruimte zonder ladingen hebben we in §6
gevonden:
L' = L
M' = γ. (M +  .
Z) .
Z)
N' = γ. (N –  .
Y) .
Y)
We gaan nu, als voorbeeld, alleen transformatie van de x–component van de laatste van
de Maxwellvergelijkingen in een ruimte mét ladingen en stromen
uitwerken, dus de vergelijking:
rot B = 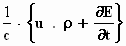 .
.
Om in het spoor van Einstein te blijven, zetten we hem even in de
andere volgorde: 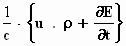 =
rot B.
=
rot B.
De x – component hiervan ziet er als volgt uit:
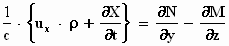
Je ziet dat ρ niet als
component wordt geschreven. De ladingsdichtheid is namelijk geen vector. Op
één plaats heeft de ladingsdichtheid slechts één waarde waar geen richting
aan kan worden toegekend. Daarom kan ρ
niet ontbonden worden.
Voor ρ mogen we schrijven
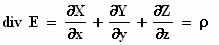
Verder maken we er gebruik van dat het differentiëren naar x (en ook
naar t) in het stelsel-in-beweging een differentiatie naar ξ
en τ wordt, waardoor we de
volgende differentiatie moeten gebruiken:
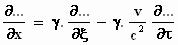
Op de plaats van de drie puntjes mag je een willekeurige fysische grootheid
lezen, bijvoorbeeld de x–component X van de elektrische
veldsterkte E (zie ook de formule "patroon" halverwege §6
voor uitleg).
Voor het differentiëren naar de tijd t in het stelsel-in-rust geldt
iets dergelijks. In het stelsel-in-beweging komt het neer op een differentiatie
naar ξ en τ:
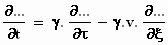
Verder is het prettig te weten dat differentiëren naar y gelijk staat
aan differentiëren naar η (en
omgekeerd) en dat differentiëren naar z gelijk staat aan differentiëren
naar ζ (en omgekeerd), omdat y
= η en z = ζ.
Met het gereedschap dat ons nu ter beschikking staat, gaan we aan de slag:
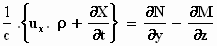
Vul de bovengenoemde uitdrukking voor div E (= ρ)
in:
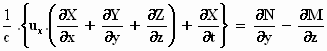
Maak gebruik van de differentiatie naar ξ
en τ in plaats van naar x
en naar t , zoals net is aangegeven, en vervang de differentiatie naar y
en z door die naar η en ζ.
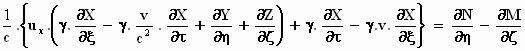
Zet de afgeleiden naar ξ, τ aan
de linkerkant en naar η en ζ
aan de rechterkant bij elkaar:
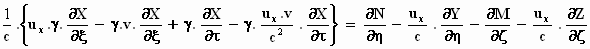
en zet tussen haakjes wat bij elkaar hoort:
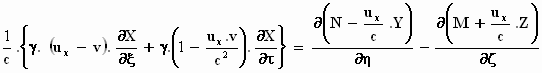
We delen de hele reutemeteut door  : :
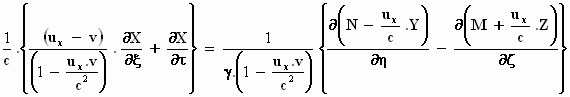
Omdat X' = X mogen we  en
en 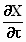 vervangen door vervangen door 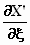 en
en 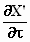 . Dus . Dus
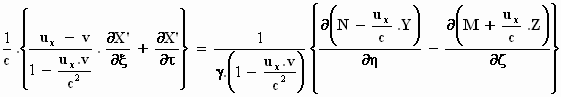
We beginnen hier vaag de contouren te ontdekken van de formule die we zoeken.
Met name de term 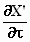 staat
al op zijn plaats. We tellen nu bij staat
al op zijn plaats. We tellen nu bij  gewoon
de twee termen op die nodig zijn om div E' te kunnen vormen: gewoon
de twee termen op die nodig zijn om div E' te kunnen vormen: 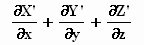 =
ρ' voor het stelsel-in-beweging
en we tellen uiteraard aan de rechterkant van het =teken dezelfde
uitdrukkingen op. =
ρ' voor het stelsel-in-beweging
en we tellen uiteraard aan de rechterkant van het =teken dezelfde
uitdrukkingen op.
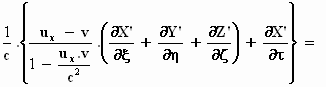
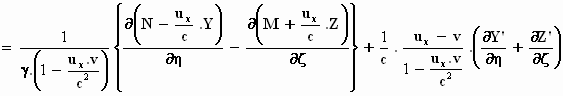
of:
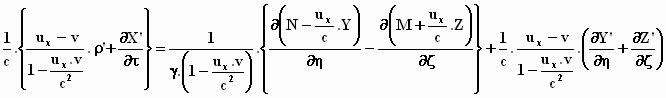
Links van het =teken heeft de vergelijking de gewenste vorm, mits we
de uitdrukking 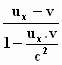 als de snelheid uξ in
het stelsel-in-beweging opvatten. Deze uitdrukking is precies de formule voor
het optellen van snelheden (§5) voor de snelheid in het stelsel-in-beweging.
als de snelheid uξ in
het stelsel-in-beweging opvatten. Deze uitdrukking is precies de formule voor
het optellen van snelheden (§5) voor de snelheid in het stelsel-in-beweging.
Terug
We werken nu verder de rechterkant van de vergelijking uit en zetten eerst de
allerlaatste term binnen de accolades.
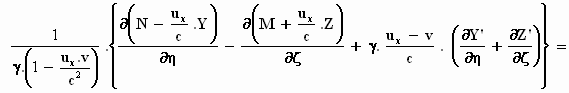
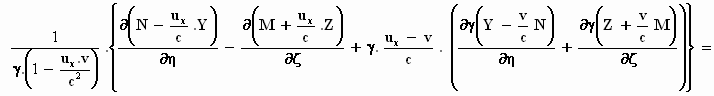
Hier moet mij even van het hart dat die Einstein wel gek
leek. Het is niet te geloven in wat voor formulewarboel je hier terechtkomt.
En dat voor een paragraaf die in het origineel maar anderhalve bladzijde groot is. Kijk maar
hoe het verder gaat.En die Einstein en zijn tijdgenoten zaten dat soort zaken
allemaal uit te puzzelen. Hadden ze niets beters te doen!?
We moeten de formules zelfs heel klein schrijven om te zorgen dat ze op één
regel passen! En dan lukt het zelfs niet altijd.
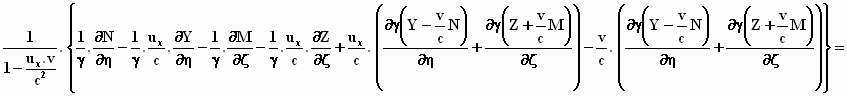
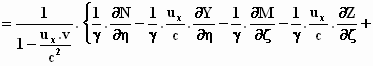
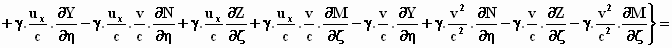
We zetten de termen bij elkaar
die dezelfde afgeleide bevatten:
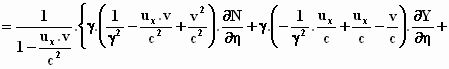
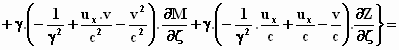
We werken dit uit door voor 1/γ2
te schrijven 1– v2/c2 (omdat dit nou eenmaal
hetzelfde is):
Er valt dan wat weg en we houden over:
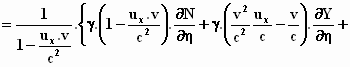
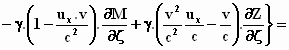
Nu is 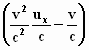 gelijk aan gelijk aan 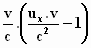 ,
zodat, zoals iedereen kan zien, de term ,
zodat, zoals iedereen kan zien, de term 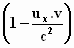 voor de accolade kan worden gezet:
voor de accolade kan worden gezet:

Terug
Als we nu weer het linker deel van de vergelijking ervoor zetten, krijgen we
een vergelijking die in enkele stappen naar het eindresultaat leidt:
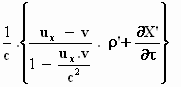 
of
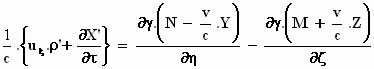
Hierin is
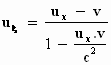
Verder zie je waarschijnlijk tot je blijdschap dat
γ . (N –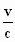 .Y)
= N'
en dat .Y)
= N'
en dat
γ . (M + 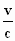 .
Z) = M',
zodat: .
Z) = M',
zodat:
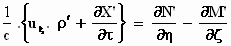 . .
Dat is hem, de x-component van de vierde Maxwellvergelijking! Als je dat van tevoren had geweten, was je er nooit aan begonnen.
Niet te geloven dat Einstein dit allemaal uit vrije wil zat uit te vogelen?
Je ziet dat deze vergelijking tussen natuurkundige grootheden voor het
stelsel-in-beweging precies dezelfde vorm heeft als de vergelijking:
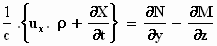
die voor het stelsel-in-rust geldt. Precies wat Einstein wilde aantonen: de
Maxwellvergelijkingen in hun meest algemene vorm voldoen aan het
relativiteitsprincipe.
Aan de echte liefhebbers laten we het over om de vergelijkingen voor de y–richting
en de z–richting na te rekenen en ook neem dan ook even derde
Maxwellvergelijking mee als je toch niets te doen hebt.
Eén vergelijking doen we nog gezamenlijk,
namelijk die voor de ladingsdichtheid ρ:

Deze vergelijking staat los van de andere. Wat is de bedoeling van deze
toevoeging?
Wij zullen hem eerst controleren.
We maken weer gebruik van de transformatieformules van blz. 1 en 2 van deze
paragraaf.
Dat ρ' gelijk is aan 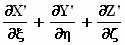 ,
daar hoeven we ons niet druk over te maken, dat is natuurlijk zo omdat ρ'
zo moet worden gedefinieerd in het stelsel-in-beweging omdat we in het
stelsel-in-rust de ladingsdichtheid ρ
ook zo hebben gedefinieerd (= met elkaar hebben afgesproken): ,
daar hoeven we ons niet druk over te maken, dat is natuurlijk zo omdat ρ'
zo moet worden gedefinieerd in het stelsel-in-beweging omdat we in het
stelsel-in-rust de ladingsdichtheid ρ
ook zo hebben gedefinieerd (= met elkaar hebben afgesproken):
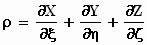 . .
We werken 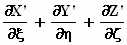 uit met de transformatieformules van §6:
uit met de transformatieformules van §6:
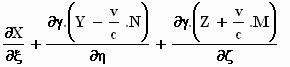
en vervolgens maken we gebruik van
x= γ. (ξ+v.τ);
y =
η; z =
ζ; t =
γ. (τ +  )
en )
en 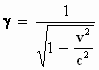
omdat we naar x, y, z en t willen differentiëren (in plaats
van naar ξ, η, ζ, τ).
Dan wordt het:
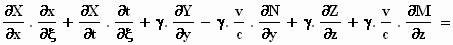
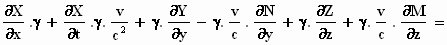
als we de termen iets anders rangschikken:
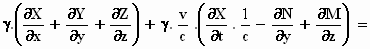
De eerste term die tussen haakjes staat, moeten we herkennen als de
ladingsdichtheid ρ en de tweede
term bevat grote delen van de vergelijking voor de x–component van het
elektrische veld:
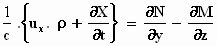
waaruit volgt:

Zo kunnen we de som van die twee termen schrijven als:
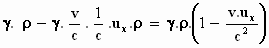 , dus , dus
Einstein heeft gelijk:
ρ' = γ. 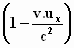 .
ρ. .
ρ.
Echte fouten maakte hij niet, van die fouten waarbij je
denkt: "Stom, stom, stom, hoe haalt hij het in zijn hoofd!"
Een zekere bewondering voor die zesentwintigjarige
snuiter is niet misplaatst.
De conclusie die Einstein aan deze relatie tussen ρ'
en ρ verbindt, is dat als de elektrische lading
van een – met willekeurige snelheid bewegend – voorwerp onveranderlijk is,
gezien vanuit een met het voorwerp meebewegend stelsel, dan is het dat ook in
het stelsel-in-rust.
Dat is uit die laatste relatie eenvoudig af te leiden, volgens Einstein….. Nou,
dat kennen we, zulke opmerkingen.
Wat bedoelt hij eigenlijk? Spreekt dat niet vanzelf?
In de voorgaande formules komt alleen de ladingsdichtheid (= lading per
volume-eenheid) voor. De lading waar Einstein over spreekt, wordt verkregen door
in gedachten een volume rond het voorwerp te nemen en het volume te
vermenigvuldigen met de ladingsdichtheid. Kennelijk moeten we het veranderde
volume van een bol in het stelsel-in-beweging in deze beschouwing betrekken..
Als het stelsel met de lading meebeweegt, dan is ux = 0 .
De lading heeft in het stelsel–in–beweging geen snelheid, maar wél ten
opzichte van een waarnemer in het stelsel-in-rust. Dan geldt voor de
ladingsdichtheid ρ':
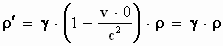
De ladingsdichtheid ρ' in het
stelsel-in-beweging is groter dan de ladingsdichtheid ρ
in het stelsel-in-rust.
We weten dat een volume in de bewegingsrichting wordt afgeplat (zie §4).
Voor een volume V' in het stelsel-in-beweging geldt 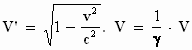 , waarbij V het volume in het stelsel-in-rust is.
, waarbij V het volume in het stelsel-in-rust is.
Het volume V' in het stelsel-in-beweging is kleiner dan
het volume V in het stelsel-in-rust.
De lading Q binnen het volume is gelijk aan de ladingsdichtheid maal
het volume, dus voor de lading Q' binnen een bewegend volume vinden we:

De lading binnen een volume in het stelsel-in-beweging is even groot als de
lading binnen datzelfde volume gezien in een stelsel-in-rust.
Einstein noemt dit een belangrijke stelling. Hoe wist hij dat dit
belangrijk is?
Hij geeft ermee aan dat de elektrische lading Q een invariante
grootheid is onder de Lorentztransformaties. Daar zijn we blij mee want in
§ 6 blz. 10 maakten we al gebruik van de constantheid van de lading – onder
enig gemopper – terwijl we er nog geen zekerheid over hadden. Het
relativiteitsprincipe vereist de gelijkvormigheid van formules, de covariantie,
maar waarom de ene grootheid zijn waarde behoudt en de andere niet, volgt niet
uit het relativiteitsprincipe. Voor elektrische ladingen was uit het
experiment al bekend dat de lading invariant is. Einstein leidt het
hier af uit de covariante transformatie van de uitgebreide
Maxwellvergelijkingen. Op een eerder moment heeft hij ook al gebruik gemaakt
van het invariant zijn van een grootheid, namelijk bij de afleiding van de
hoek φ', waaronder
een vlakke golf wordt gezien vanuit een stelsel–in–beweging ten opzichte
van de hoek φ
in een stelsel–in–rust. Daar werd, zonder bewijs (zie Uitleg§7,blz6)
, de fasehoek Φ
als invariante grootheid gehanteerd.
In §6 heeft Einstein laten zien dat het elektrisch veld en het magnetisch
veld afhankelijk zijn van de bewegingstoestand, en dus niet–invariant zijn,
in §8 laat hij zien dat de energie van een bundel niet–invariant is
en in de komende paragraaf (§10) zal hij laten zien dat de massa evenmin
invariant is.
Welke fysische betekenis kunnen we aan het invariant zijn van een grootheid
hechten?
Daarover blijven we u vooralsnog het antwoord schuldig! Eén ding is zeker: in
de moderne natuurkunde spelen de eigenschappen invariantie en covariantie
een cruciale rol.
Terug
|
