Na enige tijd heeft het elektron een snelheid v
verkregen. Aan welke bewegingswet zal het elektron in het tijdsbestek dat hier
onmiddellijk op volgt, voldoen?
We mogen en zullen aannemen, zonder de algemene geldigheid
van de beschouwing daarmee aan te tasten dat, op het moment waarop we het in
ogenschouw nemen, het elektron zich in de oorsprong van het
coördinatenstelsel bevindt en
zich met de snelheid v langs de X–as van
het stelsel K beweegt. Het spreekt voor zich dat het elektron dan
op dat moment (t = 0) in rust is ten opzichte van een met de
snelheid v parallel langs de X–as bewegend
coördinatenstelsel k .
Uit deze aanname, indachtig het relativiteitsprincipe, is
het duidelijk dat het elektron, gezien vanuit het stelsel k , in
de onmiddellijk daarop volgende tijd (voor kleine waarden van t)
zal bewegen volgens de vergelijkingen:
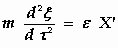
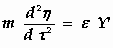
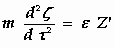
waarbij de symbolen ξ , η , ζ , τ , X ', Y ', Z '
bij het stelsel k behoren. Als we verder afspreken dat voor t
= x = y = z = 0 ook τ = ξ = η = ζ = 0 is,
dan kunnen de transformatieformules van de §§ 3 en 6 worden toegepast. Er
geldt:
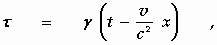
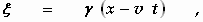


X ' = X
Y ' = γ ( Y – 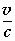 N
)
N
)
Z ' = γ ( Z + 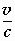 M
)
M
)
Met behulp van deze formules transformeren we de
bovenstaande bewegingsvergelijkingen van stelsel k naar stelsel K
. Dat levert op:
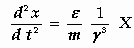 ,
,
(A) 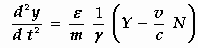 ,
,
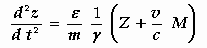 .
.
We stellen ons nu de vraag, waarbij we de gebruikelijke
beschouwingswijze volgen, welke waarde aan de "longitudinale" en welke
aan de "transversale" massa van het bewegende elektron moet worden toegekend. We schrijven de vergelijkingen
(A) in de vorm
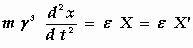
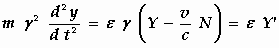
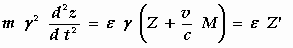
en merken vervolgens op dat ε X ' , ε Y ' , ε Z '
de componenten zijn van de op de trage massa van het elektron werkende
kracht, uiteraard beschouwd vanuit een stelsel dat op het betreffende moment met
dezelfde snelheid als het elektron beweegt. (Deze kracht zou bijvoorbeeld met
een in het stelsel-in-beweging in rust zijnde veerbalans kunnen worden gemeten.)
Wanneer we deze kracht nu eenvoudigweg "de kracht die op het elektron
werkt" noemen en uitgaan van de vergelijking
Massa x Versnelling = Kracht
en als we verder afspreken dat de versnellingen in het stelsel-in-rust K
gemeten worden, dan verkrijgen we uit bovenstaande vergelijkingen:
De longitudinale massa = 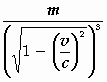
De transversale massa =
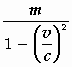
Natuurlijk zou men bij een andere definitie
van de kracht en de versnelling andere waarden voor de massa’s verkrijgen; men
ziet daaruit dat men bij een vergelijking van verschillende theorieën over de
beweging van het elektron grote voorzichtigheid moet betrachten.
We merken op dat het resultaat betreffende de massa ook
voor een materiepunt dat uit zware massa bestaat, geldt, want van een
dergelijk materiepunt kan door het aanbrengen van een willekeurig kleine,
elektrische lading een elektron – volgens onze definitie – worden gemaakt.
We zullen nu de kinetische energie van het elektron
bepalen. Wanneer een elektron met een beginsnelheid 0 vanaf de oorsprong
van het stelsel K precies langs de X – as beweegt
door de
werking van een elektrostatische kracht X, dan is
het duidelijk dat de energie die aan het elektrostatische veld wordt onttrokken
de waarde ∫ ε X dx
heeft. Als het elektron slechts
langzaam wordt versneld en dientengevolge geen energie in de vorm van straling
kan afgeven, moet de aan het elektrostatische veld onttrokken energie gelijk
worden gesteld aan de bewegingsenergie W van het elektron. Men
verkrijgt dan, bedenkende dat gedurende de gehele in beschouwing genomen
beweging de eerste van de vergelijkingen (A) geldt: