|
Bijlage bij §4:
" Verleden, Heden en Toekomst"
Naar Uitleg §5 Optellen
Naar Uitleg §4 Effect op lengte en tijd
Naar Uitleg
Inhoud
Naar Centrale Hal
Wie zich al eerder verdiept heeft in de Relativiteitstheorie of in de
Kosmologie, zal indrukwekkende tekeningen zijn tegenkomen die de samenhang
tussen tijd en ruimte verbeelden. Uitermate fraai ogende, ruimtelijke figuren
die het verleden via het heden met de toekomst verbinden (zie figuur 411).
Zie bijvoorbeeld de boeken van: Penrose p.189–213; Hawking p.40 – 44 ; Bondi
p.143; Davies p.67 – 87 . Voor nadere informatie over de boeken: zie de
rubriek "boeken".
Hoe moet een dergelijke figuur worden gelezen?
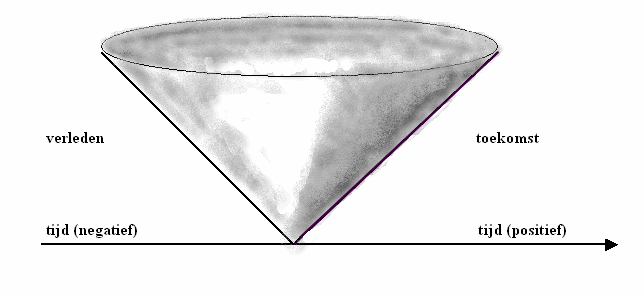
Figuur 411 Ruimte en tijd
Het gaat om een hele slimme uitbreiding van onze veel gebruikte driehoeken
met de bekende verhoudingen. Om dat duidelijk te maken, moeten we bij het begin
beginnen.
We hebben gezien aan het eind van § 2plus bij de afleiding van de formule "te
vlug geschoten" dat je leuke resultaten krijgt als je de balk in het
stelsel–in–rust scheef op de balk in het stelsel–in–beweging tekent (zie
figuur 228).
In figuur 412 zijn de twee stelsels getekend met de assen scheef op
elkaar. Een stelsel-in-rust met een x-as en een t-as en een
stelsel-in-beweging met een ξ-as
en τ-as. De x–as en de ξ–
as staan ongeveer verticaal.
De assen staan op een zodanige manier scheef op elkaar dat als we een
loodlijn van de ene as op de andere overeenkomstige as neerlaten er altijd weer
zo’n driehoek met de bekende verhoudingen c : √(c2 – v2)
: v wordt gevormd, of anders geschreven door de drie termen ieder door c
te delen:
1
: 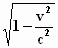 :
: 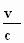 .
.
De beide stelsels zijn getekend voor het moment t = τ
= 0. De oorsprong O van beide stelsels valt samen. Dat is een
momentopname. Enige tijd later, op het tijdstip τ
= τ*, is het nulpunt van de ξ
–as langs de τ–as verschoven
tot het punt τ = τ*. De
gehele ξ –as (stippellijn) is verschoven. Op
het tijdstip τ* heeft het nulpunt van de ξ–as
de waarde (τ*, 0). Je ziet dat
de ξ–as scheef op de t–as
staat zodat ieder punt van de ξ–as
met een andere tijd t overeenkomt. Maar, een toenemende ξ
correspondeert met een toenemende tijd t. Dat is niet in
overeenstemming met onze eerdere bevindingen. We komen direct met een oplossing.
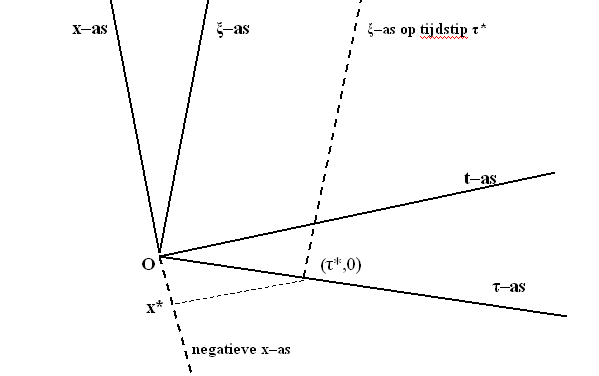
Figuur 412 Twee scheef op elkaar staande stelsels.
Als je vanuit het punt met de coördinaten (τ*,
0) een loodlijn neerlaat op de x-as vind je de x–coördinaat
x* . Dus de oorsprong van het stelsel-in-beweging heeft zich langs de x–as
van het stelsel-in-rust verplaatst van x = 0 tot x = x* .
Daar klopt alweer iets niet. De oorsprong van het stelsel-in-beweging heeft
zich in de negatieve richting verplaatst terwijl deze een positieve
snelheid had. Daar zijn we vanuit gegaan.
Als je verder zou uitzoeken hoe het zit met de coördinaten van een willekeurig
punt P blijken die niet te voldoen aan de transformatieformules.
"Leiden in last!", zou je denken. Maar er is een verbluffend
handige manier om de problemen te verhelpen: Verwissel de x-as en de ξ-
as ! Dat hebben we gedaan in figuur 413.
 | We spreken af dat de coördinaten van een punt worden gevonden door vanuit
dat punt de loodlijnen neer te laten op de assen, welke assen dat ook zijn,
daarin is niets veranderd. |
We bekijken een punt op de t –as: t*(zie figuur 413).
In dat punt is de ξ –waarde: 0.
Dus zit de ξ – as op die plek
(zie stippellijn). Als we nu een loodlijn neerlaten op de x – as
krijgen we het punt x* . Die heeft nu een positieve waarde. Het nulpunt
van het stelsel-in-beweging heeft zich dus in t* seconde verplaatst naar x*.
Als we vervolgens vanuit t* de loodlijn neerlaten op de τ–as
krijgen we het punt τ*. De
verplaatsing in het stelsel-in-beweging duurde τ*
seconde. Zoals je ziet is τ*
kleiner dan t* en omdat de driehoek Ot*τ*
de bekende verhoudingen heeft, is τ* = t*/γ.
Dat zit dus wel goed.
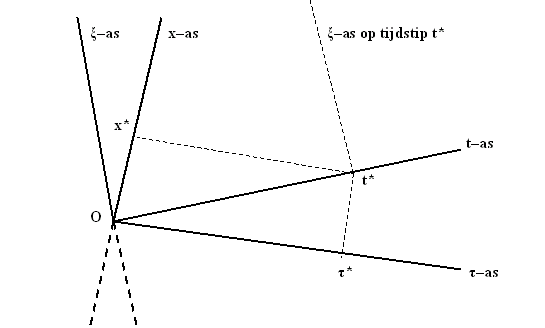
Figuur 413 De x-as en de ξ-as zijn verwisseld.
Menigeen zal met de vraag zitten of dat zo maar kan: een assenstelsel waarvan
de assen niet loodrecht op elkaar staan. In figuur 414 lichten we dat
toe. In die figuur staat de x-as schuin op de t-as en de ξ
– as schuin op τ – as .
Waarom dit geen probleem is, wordt duidelijk als je ziet dat de plaats van een
willekeurig punt P in het stelsel ondubbelzinnig wordt vastgelegd door
vanuit P de loodlijnen neer te laten op de assen van het stelsel. Er is
geen tweede punt dat dezelfde coördinaten xP en tP
in het stelsel-in-rust kan krijgen als het punt P. Ook de coördinaten ξP
en τP in het
stelsel-in-beweging zijn in dat stelsel de enige coördinaten die P kan
krijgen. Dus ook met scheve assen wordt ieder punt op een unieke manier
vastgelegd.
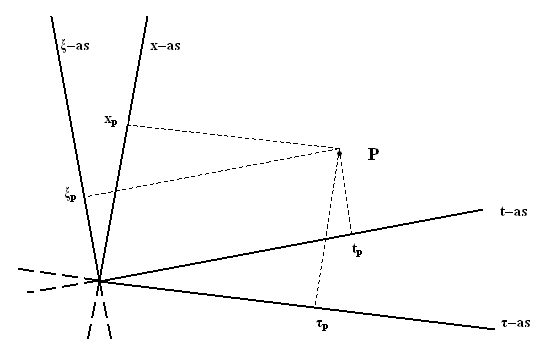
Figuur 414 De plaats van het punt P ligt in beide stelsels eenduidig vast
In de volgende figuur (fig. 415) hebben we nogmaals van het punt P
de coördinaten xP en tP in het
stelsel-in-rust en de coördinaten ξP
en τP in het
stelsel-in-beweging aangegeven.
We kunnen nu via eenvoudige meetkunde laten zien dat voor ξP
en τP de
transformatieformules gelden:
ξP
= γ ( x – v . t)
en τP = γ
( t – 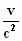 . x) . x)
Daartoe trekken we twee hulplijnen, namelijk van xP naar Q
en van tP naar R. Het parallellogram ORPQ dat nu
is ontstaan, bevat verschillende driehoeken met de bekende verhoudingen. We
hebben nog een hulplijn nodig: de loodlijn vanuit tP op de x–as.
Dat snijpunt noemen we S . Hiermee gaan we aan de slag. Eerst zullen we
de afstand ξP
uitdrukken in xP en tP.
Het punt S is de plaats op de x- as waar het nulpunt van
de ξ-as zich bevindt na tP
seconde. Dit nulpunt beweegt met de snelheid v langs de x–as,
dus geldt OS = v .tP .
De afstand van S tot xP is dus xP –
v . tP . Wanneer je nu de afstand PT van P tot de
lijn die van S naar tP loopt, bekijkt, dan geldt ook PT
= xP – v . tP.
We bekijken nu de driehoek PTtP. Daarin is de afstand van P
tot tP een factor γ
keer groter (wegens die bekende verhoudingen) dan de afstand van P tot T
, dus PtP = γ. (xP
– v . tP).
Ter herinnering: γ = 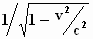
De afstand van O tot ξP
is gelijk aan de afstand van P tot tP , dus de waarde
van de coördinaat ξP
is γ ( xP – v . tP)
.
De transformatie naar ξ is
geslaagd: ξP =
γ ( xP – v . tP)
Voor de transformatie naar τ
moeten we eerst inzien dat de lijnstukken van Q naar xP
en van R naar τP
gelijk aan elkaar zijn. In de driehoek OxPQ is de lengte van O
naar Q gelijk aan γ . xP
en de lengte van Q naar xP is 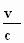 .
γ. xP. Vervolgens maken
we ervan gebruik dat als je een afstand in zo’n figuur als tijd wil
uitdrukken, de afstand nog eens door c moest worden gedeeld (zie .
γ. xP. Vervolgens maken
we ervan gebruik dat als je een afstand in zo’n figuur als tijd wil
uitdrukken, de afstand nog eens door c moest worden gedeeld (zie
§2plus). Zo komen we op een tijdsbestek tussen de punten R en τP
op de τ-as gelijk aan 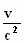 .
γ. xP. Verder is de tijd
van O tot R gelijk aan γ . tP
. .
γ. xP. Verder is de tijd
van O tot R gelijk aan γ . tP
.
De waarde van de coördinaat τP
wordt dan gelijk aan γ . tP
– 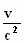 .
γ. xP , dus .
γ. xP , dus
τP = γ
. (tP – 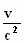 .
xP ). .
xP ).
Ook de transformatie naar τ
klopt als een bus!
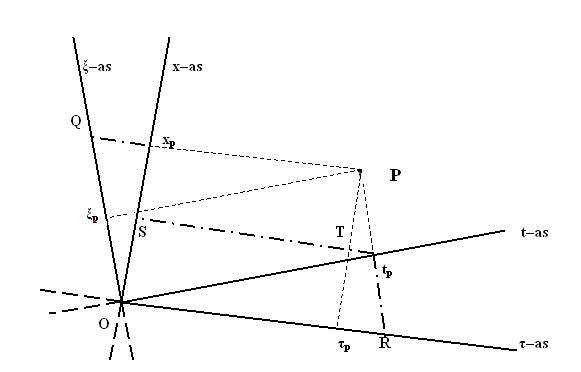
Figuur 415 De tekening geeft de transformaties correct weer
We gaan nu nog een stapje verder. Voor de afstand zullen we als maat de lichtseconde
gebruiken, dat is de afstand die het licht in 1 seconde aflegt: c meter
of 3 x 108 m. Als maat voor de tijd wordt gewoon de seconde
genomen. In figuur 416 is dit aangegeven. De maatstrepen bevinden zich
even ver van de oorsprong, of je nu in het stelsel-in-rust kijkt of in het
stelsel-in-beweging.
Een dergelijk ruimte–tijd diagram wordt een Lorentzdiagram
genoemd.
De stippellijn waar het diagram symmetrisch omheen ligt, geeft de
verplaatsing aan van een lichtsignaal. Dit diagram laat zien dat na een zelfde
tijd in beide stelsels het licht eenzelfde afstand heeft afgelegd. Kijk maar,
bijvoorbeeld bij het tijdstip 2 seconde op de t–as vind je via
de stippellijn het punt P en daar vandaan op de x–as de afstand 6
x 108 m . Neem je het tijdstip 2 seconde op de τ–as
van het stelsel-in-beweging dan vind je via de stippellijn het punt P* en
daar vandaan op de ξ–as
eveneens de afstand 6 x 108 m.
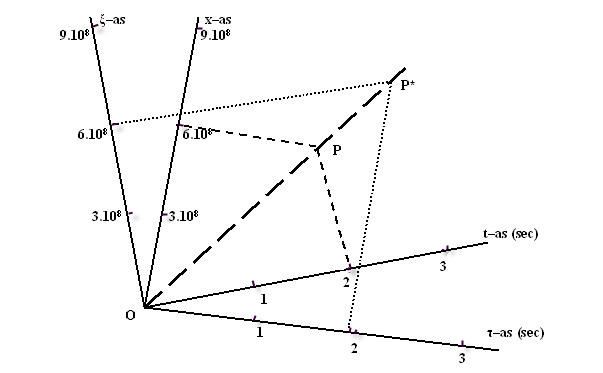
Figuur 416 Het Lorentzdiagram
Een punt E (zie fig. 417) in het vlak van een Lorentzdiagram
noemen we een puntgebeurtenis E (de eerste letter van het Engelse
"Event" ). Het is iets dat zich op dát moment dáár bevindt,
los van het stelsel van waaruit het wordt bekeken. Een assenstelsel is immers
alleen maar iets abstracts dat we ons in de ruimte denken om de gebeurtenis te
kunnen omschrijven: "welk moment" en "waar" vindt de
puntgebeurtenis plaats. Met een ander assenstelsel vind je een andere tijd en
een andere plaats. Soms gebruikt men in plaats van "assenstelsel" de
term "referentiestelsel", waarmee goed wordt uitgedrukt dat de
coördinaten die je vindt afhankelijk zijn van het stelsel. Het
woord "gebeurtenis" overigens suggereert meer dan er in het algemeen
aan de hand is.

Figuur 417 De coördinaten van een puntgebeurtenis E in
een Lorentzdiagram
Van een willekeurige puntgebeurtenis E kunnen de coördinaten xE
en tE in het stelsel-in-rust en de coördinaten ξE
en τE in het
stelsel-in-beweging worden afgelezen langs de assen door vanuit E
loodlijnen op die assen neer te laten.
In de volgende figuur (Fig. 418) geven we een stilstaand voorwerp aan
bij P op de ξ–as van
het stelsel-in-beweging met de coördinaat ξP
. Hoewel het stilstaat op de ξ-as
gaat de tijd onverdroten voort. Daarom levert een stilstaand voorwerp geen punt
in het diagram, maar een lijn. De lijn is loodrecht op de ξ–as
getekend van P naar Q zodat zijn ξ–coördinaat
in de loop der tijd constant blijft.
De tijd neemt voortdurend toe, zowel in het stelsel-in-rust als in het
stelsel-in-beweging. Voor het voorwerp geldt als het zich in het punt P
bevindt in het stelsel-in-rust t = 0 sec en als het zich in het punt Q
bevindt t = tQ sec. In het stelsel-in-beweging vind je
langs de τ-as geheel andere
tijden, namelijk τP
en τQ.
Het tijdverschil voor de punten P en Q in het stelsel-in-rust
is tQ – 0 = tQ. In het stelsel-in-beweging
is het tijdverschil τQ
– τP.
 | Oefening 18
Het is niet moeilijk aan te tonen, maar probeer het eens, dat het laatste
tijdverschil γ keer kleiner is dan het
eerste, precies wat we verwachten, want de tijd in het
stelsel-in-beweging is γ
keer trager dan de tijd in het stelsel-in-rust. |
De ξ–coördinaat ξP
is constant, maar de x–coördinaat is dat geenszins. Het voorwerp
bevindt zich in een vast punt in het bewegende stelsel, maar verplaatst zich in
het stelsel-in-rust in de tijd tQ van xP
naar xQ. Het bevindt zich niet voor niets het
stelsel-in-beweging. De afstand van xP naar xQ
is gelijk aan v. tQ.
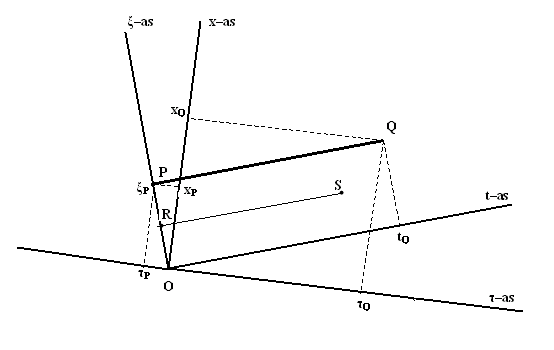
Figuur 418 Stilstaand voorwerp in het stelsel-in-beweging
verplaatst zich in het stelsel-in-rust
Een lijn in een Lorentzdiagram geeft de plaats aan die een voorwerp in de
loop van de tijd inneemt in het vlak van ruimte en tijd. Zo’n lijn wordt een ‘wereldlijn’
genoemd. Een wereldlijn hoeft niet loodrecht op een as te staan (dat geldt
alleen voor een stilstaand voorwerp) en hoeft evenmin een rechte lijn te zijn
(dat is alleen het geval voor een voorwerp in een eenparige rechtlijnige
beweging).
In dezelfde figuur 418 is met de lijn van R naar S de
wereldlijn aangegeven van een voorwerp dat zich dichter bij het nulpunt van de ξ-as
bevindt dan het punt P . Hieruit is te begrijpen dat de
wereldlijn van het nulpunt van de ξ-as
met de t-as samenvalt.
Redenerend vanuit een stilstaand voorwerp op de x–as is in te zien
dat in het Lorentzdiagram de wereldlijn van het nulpunt van de x–as
juist op de τ–as ligt.
We bekijken vervolgens (zie figuur 419) de wereldlijn van een
stilstaand voorwerp op de x-as. In het Lorentzdiagram bevindt het zich
eerst in het punt P en later in het punt Q. Als we nu de tijd
aflezen tussen de punten P en Q vinden we op de τ-as
de tijden τP en τQ
en op de t-as de tijden tP en tQ
. Het blijkt dat het tijdverschil op de τ-as
groter is dan op de t-as. De tijd in het stelsel-in-beweging is
groter dan die in het stelsel-in-rust. Dat hebben we nog niet eerder meegemaakt!
Kennelijk moeten we tegen een stilstaand punt in het stelsel-in-rust aankijken
vanuit het stelsel-in-beweging. Maar dan is het stelsel-in-beweging bevorderd
tot stelsel-in-rust! Dat is de kracht van het diagram: er is geen zogenaamd
"absoluut" verschil tussen een bewegend stelsel en een
stelsel-in-rust. De rollen kunnen worden omgedraaid. Het diagram geeft gewoon
twee stelsels weer die ten opzichte van elkaar in een eenparige beweging zijn. .
De coördinaten op de ξ–as
van P en Q zijn achtereenvolgens: ξP
en ξQ. Het
stilstaande voorwerp op de x – as heeft in de tijd τQ
een weg afgelegd van ξP
tot ξQ. De oorsprong
van het bewegende stelsel komt namelijk met een snelheid + v naar dat
voorwerp toe. Bedenk hierbij dat op het moment dat het voorwerp zich in P
bevond voor de tijd gold: τp
= 0.
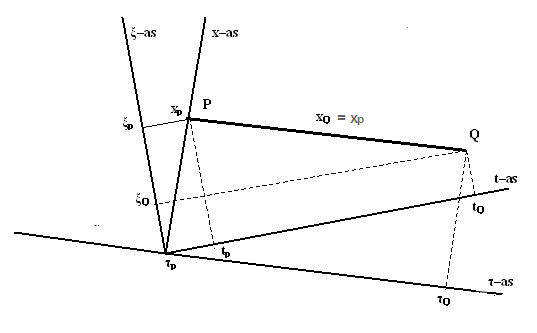
Figuur 419 De wereldlijn van een stilstaand voorwerp op de
x-as
Het volgende Lorentzdiagram (figuur 420) laat een voorwerp zien dat
met een eenparige snelheid beweegt en in geen van beide stelsels stilstaat. Voor
ieder punt van de wereldlijn zijn de coördinaten in beide stelsels af te lezen.
Voor het beginpunt P zijn bijvoorbeeld de coördinaten in het x–t–stelsel
tP en xP en in het ξ–τ–stelsel
τP en ξP.
Vervang de index P door een Q en je hebt de
coördinaten van het punt Q.
De snelheid in ieder stelsel kan worden berekend door de coördinaten van P
en die van Q uit het diagram af te lezen. Uit het quotiënt van de
afgelegde weg en de tijdsduur verkrijgen we de snelheden in elk van de stelsels:
in het x–t–stelsel 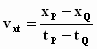 en
in het ξ–τ– stelsel en
in het ξ–τ– stelsel 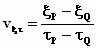 . .
Deze snelheden zijn in het algemeen niet gelijk in grootte, denk maar aan een
stilstaand voorwerp in het bewegende stelsel, dat in het stelsel–in–beweging
geen snelheid heeft en in het stelsel–in–rust een snelheid heeft die gelijk
is aan de snelheid van het stelsel–in–beweging.
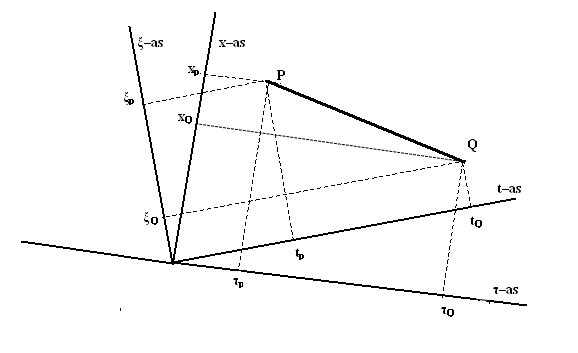
Figuur 420 Een voorwerp dat in beide stelsels eenparig
beweegt
We kunnen nu een figuur, zoals figuur 411, begrijpen. De grondslag wordt
gevormd door een Lorentzdiagram in een nog verder geëvolueerde vorm. Bekijk
maar eens het volgende Lorentzdiagram (fig. 421).
Het punt E1 stelt een puntgebeurtenis voor. Een tweede
puntgebeurtenis wordt voorgesteld door het punt E2 . Als we op
de t-as en de τ-as kijken
welke tijden bij de puntgebeurtenissen horen, dan vinden we dat de tijd t2
van de tweede gebeurtenis in het x–t–stelsel ná de tijd t1
van de eerste gebeurtenis komt. Dus in het x–t–stelsel vindt E2
ná E1 plaats.
Kijken we nu naar de tijden in het ξ–τ–stelsel
dan zien we dat τ2
vóór τ1 ligt, dus
in het ξ–τ–stelsel
vindt E2 vóór E1 plaats. Deze bevinding
geldt voor het gehele grijze gebied boven E1 . In het grijze
gebied beneden E1 geldt het omgekeerde.
 | Je ziet hieruit dat niet alleen het begrip gelijktijdigheid relatief is,
maar ook de begrippen eerder en later. Voor goed begrip moet je wel voor
ogen houden dat het om twee puntgebeurtenissen gaat die ver van elkaar
plaatsvinden. Sommigen denken dat als iemand mij een klap geeft en ik sla
daarna, volgens oud gebruik, krachtig terug, dit vanuit een stelsel–in–beweging
kan worden gezien alsof ik eerst sloeg en dat ik daarna pas de klap kreeg.
Zo zit dat echt niet! |
Terug
 | Oefening 19
Geef aan in welk deel van de tekening je de puntgebeurtenissen vindt die in
het x–t–stelsel vóór E1 plaatsvonden. |
Dat de punten, die op de rand van het grijze gebied liggen, de gebeurtenissen
voorstellen die in de tijd samenvallen met de eerste gebeurtenis had je
natuurlijk zelf al bedacht. Daarvoor geldt dat de punten op (het verlengde van)
de lijn E1t1 gelijktijdig zijn in het x–t–stelsel
en dat de punten op de lijn E1τ1
gelijktijdig zijn in het ξ–τ–stelsel.
Wanneer E2 zich buiten het grijze gebied bevindt, is
de volgorde in de tijd voor de twee gebeurtenissen in beide
stelsels hetzelfde, maar het tijdverschil tussen beide gebeurtenissen wordt in
de twee stelsels verschillend waargenomen..
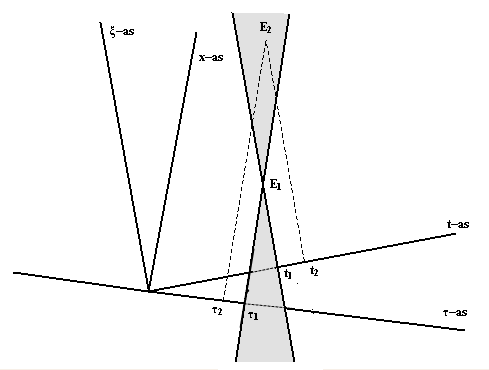
Figuur 421 De gebeurtenis E2
vindt in het ene stelsel eerder plaats dan E1 en in het
andere stelsel juist later
We moeten goed in gedachten houden dat in dit diagram gelijktijdig betekent
gelijktijdig volgens het recept van Einstein: een lichtstraal die even veel tijd
nodig heeft voor de heenweg als voor de terugweg. Het gaat er dus niet om welke
gebeurtenis we het eerst waarnemen, want dat hangt af van de
afstand tot de gebeurtenis, van de tijd die het licht nodig heeft ons te
bereiken.
 | Onthoud: Er is een groot
verschil tussen "gelijktijdig zijn en gelijktijdig zien" |
 | Oefening 20
In het volgende Lorentzdiagram is E1 een puntgebeurtenis die we
voor het gemak in de oorsprong van de stelsels hebben geplaatst. Dus x = ξ
= t = τ = 0. De schaalverdeling langs de tijd–assen is in seconde en
langs de lengte–assen in 3x108 meter. De ξ–as
beweegt met een snelheid van 0,2xc (met c = lichtsnelheid van 3x108
m/s) in de positieve richting langs de x–as. Het gebied waar
gebeurtenissen zowel vóór als ná E1 kunnen plaatsvinden, is
het gebied tussen de x-as en de ξ–as.
Een tweede puntgebeurtenis E2 is precies op de ξ–as
gesitueerd (zie figuur B412) op de plaats 24x108 m. |
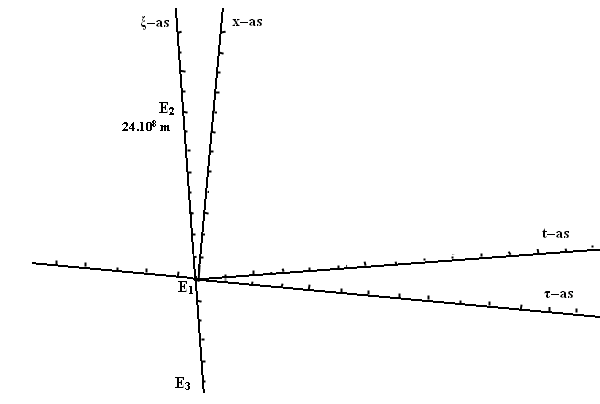
Figuur 422 bij oefening 20
Vragen:
* In welk stelsel is E2 gelijktijdig met E1?
* Hoeveel eerder vindt E2 plaats in het ander
stelsel dan E1?
In E3 op de ξ–as
bevindt zich op t = 0 een waarnemer in het stelsel-in-beweging op een
afstand van 15x108 m van de puntgebeurtenis E1.
* Na hoeveel tijd ontvangt E3 berichten van de
gebeurtenissen in E1 en E2, als hij hiervan met een
lichtsignaal op de hoogte wordt gebracht?
 | Voor puntgebeurtenissen waarvan de volgorde in de tijd
afhankelijk is van de bewegingstoestand van het stelsel van waaruit de
gebeurtenissen worden waargenomen, geldt dat er geen "oorzaak en gevolg
relatie" tussen de gebeurtenissen kan bestaan. Anders zouden oorzaak en
gevolg kunnen worden omgedraaid. Voor de puntgebeurtenissen E1 en
E2 in figuur 421 betekent dit dat ze zover van elkaar gelegen
zijn dat het licht in de tijd t2–t1 , noch in de
tijd τ1–τ2
, vanuit puntgebeurtenis E1 puntgebeurtenis E2 kan
bereiken of omgekeerd. |
We kunnen het verwisselen van de volgorde in de tijd misschien beter
begrijpen als we een puntgebeurtenis E2 bekijken in figuur
423 die zich tussen de t–as en de τ–as
bevindt. We nemen de puntgebeurtenis E1 in de oorsprong. Het
punt E2 bevindt zich in een vergelijkbare situatie als een
punt tussen de x–as en de ξ–as
zoals in figuur 421. Je ziet nu dat in het stelsel-in-rust het punt met x2
een plaats vóór E1 inneemt langs de positieve x–as,
terwijl dat punt in het stelsel-in-beweging zich met ξ2
achter E1 bevindt. Als beide punten stilstaan in het
stelsel-in-rust en je loopt op je gemak in positieve richting langs de positieve
x–as, dan passeer je eerst E1 en daarna neem je aan
je rechterhand E2 waar. Tijdens het waarnemen even stilstaan!
Doe je hetzelfde in het stelsel-in-beweging dan zie je aan je rechterhand eerst E2
en daarna pas E1. Het lijkt op een perspectivische vertekening
waardoor, bijvoorbeeld een cowboy in de verte, alleen al door hem afwisselend
met het linker of het rechter oog te bekijken, links of rechts van een nabij
raamspijltje kan komen te staan. Je kan dus zeggen dat je een punt in het
stelsel-in-beweging vanuit een andere hoek waarneemt dan in het stelsel-in-rust.
Datzelfde gebeurt ook met de tijd: twee punten worden vanuit een ander
tijdsperspectief bekeken.
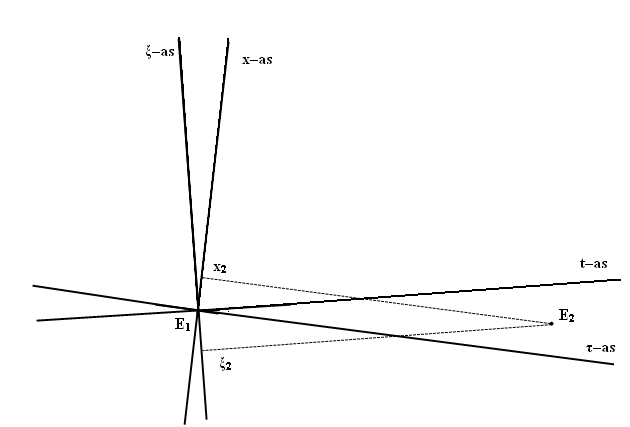
Figuur 423 Een punt E2 kan zich ook links of
rechts van E1 bevinden
Als laatste zullen we een Lorentzdiagram laten zien waarin "verleden,
heden en toekomst" worden geïllustreerd. We zetten het diagram op zoals figuur
416 en we voegen de negatieve assen toe. De gestippelde symmetrieas tussen
de positieve x–as en de positieve t–as, de 1ste
symmetrieas, geeft de plaats in het Lorentzdiagram weer van een lichtsignaal dat
vanuit de oorsprong in de positieve richting langs de x–as is
verzonden. Omdat de lijn ook symmetrisch tussen de positieve ξ–as
en de positieve τ–as ligt, mag
je ook zeggen dat het om een lichtsignaal gaat dat langs de positieve ξ–as
is verzonden. De lijn is in wezen de wereldlijn van het lichtsignaal.
Vervolgens tekenen we een stippellijn, de 2de symmetrieas, die de
wereldlijn voorstelt van een lichtsignaal dat vanuit de oorsprong in
negatieve richting langs de x-as en de ξ–as
beweegt. Deze deelt de hoek tussen de negatieve ξ–as
en de positieve τ–as in
tweeën en staat loodrecht op de eerste symmetrieas (zie figuur 424). Zo
krijgen we een compleet, maar behoorlijk onoverzichtelijk diagram.
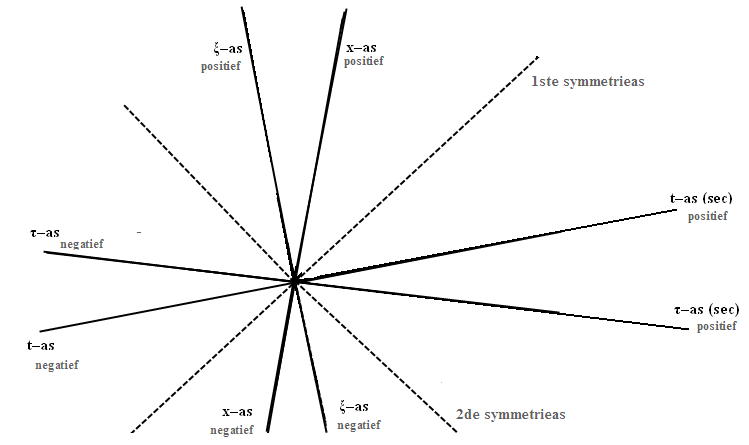
Figuur 424 Compleet Lorentzdiagram
We laten nu de tijd–assen weg. Dat ruimt op. Het gebied waar
"eerder" of "later" een relatief begrip is, geven we
donkergrijs aan. De gebieden er omheen tot aan de twee symmetrie–assen maken
we lichtgrijs en we krijgen figuur 425. Geef toe: het oogt fraai!
Het heeft ook betekenis. In het donkergrijze gebied geldt dat een
puntgebeurtenis E2 zich eerder of later had voorgedaan dan de
puntgebeurtenis E1 afhankelijk van het stelsel van waaruit het
wordt waargenomen. Verder hadden we vastgesteld dat er geen "oorzaak en
gevolg" verband kan bestaan tussen E2 en E1
want anders kan je oorzaak en gevolg omkeren.
Het lichtgrijze gebied stelt bij toenemende snelheid van het stelsel–in–beweging
de maximale uitbreiding voor van het donkergrijze gebied. Als het
stelsel-in-beweging de lichtsnelheid heeft ten opzichte van het stelsel-in-rust
dan valt de x–as samen met de 1ste symmetrie–as en de ξ–as
valt samen met de 2de symmetrieas.
Een puntgebeurtenis, die niet in één van de grijze gebieden ligt, kan nooit
gelijktijdig zijn met de gebeurtenis E1. De puntgebeurtenis E3
in het blanco gebied rechts van E1 vindt altijd
later plaats dan de gebeurtenis E1, vanuit welk snel bewegende
stelsel je het ook bekijkt en een puntgebeurtenis E4 vindt
altijd eerder plaats dan E1 van waaruit je het ook bekijkt. De
eerste gebeurtenis E1 wordt het "nu" of het "heden"
genoemd. De gebeurtenis E3 moet dan een gebeurtenis in de
"toekomst" zijn en de gebeurtenis E4
moet een gebeurtenis uit het "verleden" zijn.
De wereldlijn van een stoffelijk punt dat door "heden" gaat, kan niet in het grijze of donkere gebied komen. Daartoe zou zijn snelheid
groter dan de lichtsnelheid moeten zijn. De wereldlijn van een signaal dat met
de lichtsnelheid beweegt, valt precies samen met de symmetrieassen.
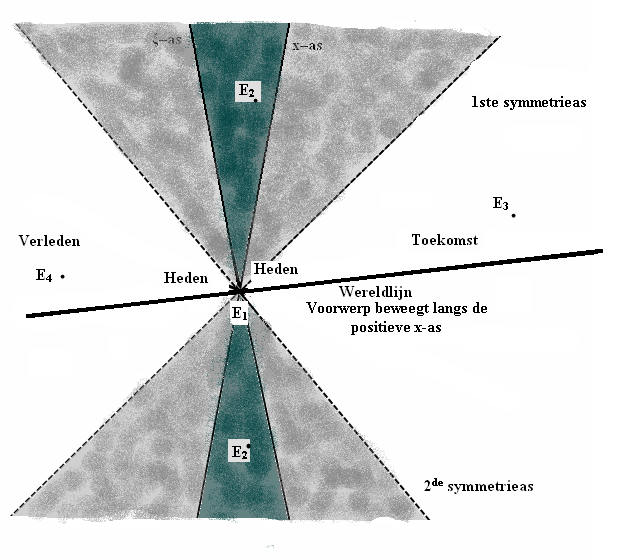
Figuur 425 Verleden, heden en toekomst
Als we in het punt E1 een lichtflits veroorzaken, zal het
licht zich bolvormig uitbreiden. In de tweedimensionale figuur 425 zal
het licht in de vorm van twee punten langs de symmetrie–assen in de richting
van de toekomst bewegen, naar rechts in de tekening.
We krijgen een suggestief beeld als we er een driedimensionaal uiterlijk aan
geven. We nemen daartoe figuur 425 en laten alleen het stelsel–in–rust
toe. Het stelsel–in–beweging laten we weg, maar we geven wel de grenzen aan
van het grijze gebied waar de begrippen eerder en later relatief zijn. Dat wordt
figuur 426.
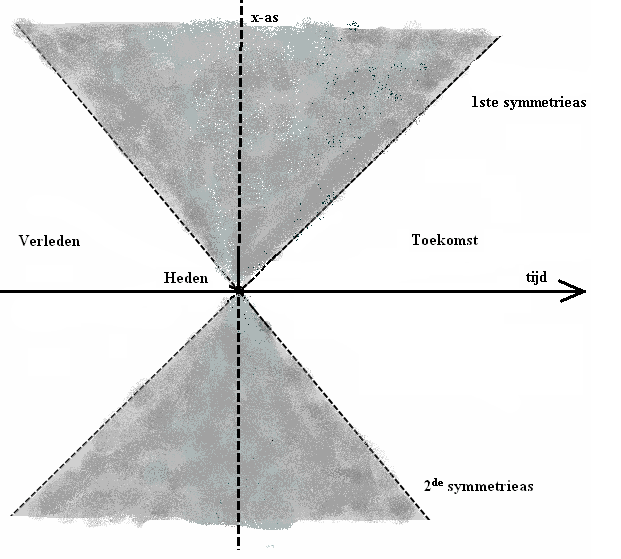
Figuur 426 De wereld vanuit het stelsel–in–rust
Vervolgens maken we er een omwentelingslichaam van door de figuur om zijn
tijd–as rond te draaien. Dan krijgen we figuur 427. De x–as
ligt nu in een vlak loodrecht op de tijd–as. Op deze manier beelden we
de tijd uit plus twee ruimtedimensies.
De heldere kegelvormige oppervlakken worden zeer toepasselijk
"lichtkegels" genoemd. Wanneer in het punt "heden" een
lichtflits wordt geproduceerd dan zal de bolvormige lichtgolf in dit
Lorentzdiagram als een steeds groter wordende cirkel langs de rand van de
lichtkegel bewegen.
De ruimte binnen de kegels is de ruimte waar de wereldlijn van een stoffelijk
punt dat het punt "heden" passeert binnen moet blijven.
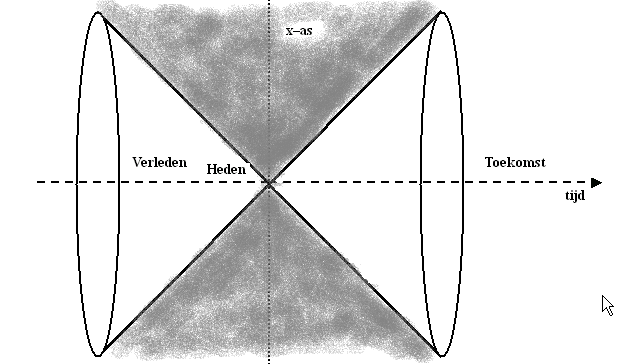
Figuur 427 Een 3D–suggestie
De ruimte buiten de lichtkegels is nog steeds het gebied waar de begrippen
"eerder" of "later" relatief zijn, afhankelijk van het
stelsel van waaruit je twee gebeurtenissen bekijkt.
Om een nog suggestiever beeld te verkrijgen, zet je de diabolo rechtop (figuur
428). Je krijgt de vorm van een zandloper. Voeg nog wat schaduweffecten toe
en je hebt een intrigerend plaatje voor de ruimte en de tijd.
In die vorm wordt de relatie tussen "Ruimte en Tijd" in de
populaire literatuur weergegeven. De tijd wijst omhoog, naar de "absolute
toekomst", het verleden beneden heet nu het "absolute verleden".
Het horizontale vlak vormt de ruimte, waarvan we slechts twee dimensies
zichtbaar kunnen maken. De lichtkegels zijn de uitdijende cirkels die gevormd
worden op het snijvlak van een bolvormige lichtuitbreiding en een plat vlak.
 | In een zandloper zou je het bovenste deel het verleden
noemen en het onderste deel de toekomst omdat de deeltjes van boven naar
beneden vallen. |
De wereldlijn van een stoffelijk punt door het "Heden" moet binnen
de grenzen van de "zandloper" worden getekend. Informatie die het punt
"Heden"bereikt, moet afkomstig zijn uit de lichtkegel "Absolute
verleden" en informatie die uit het punt "Heden" afkomstig is ,
blijft binnen de lichtkegel "Absolute toekomst".
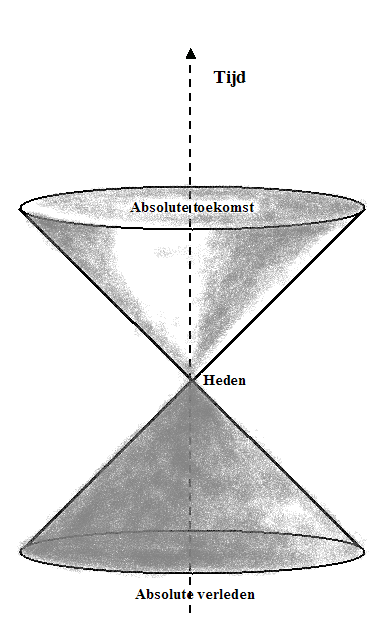
Figuur 428 Ruimte en tijd in lichtkegels gevat
De gebieden terzijde vormen de gebieden die zover verwijderd zijn van de
plaats waar het "Heden" zich bevindt dat er geen
informatie-uitwisseling plaats kan hebben gevonden in de tijd die er bij hoort.
Bijvoorbeeld: Precies opzij van het punt "Heden" geldt dezelfde tijd
als in het punt "Heden". Een gebeurtenis in het punt "Heden"
kan natuurlijk niet op hetzelfde moment ook in zo’n punt bekend zijn, want dan
zou de informatie zich met een oneindige snelheid hebben verplaatst.
Juist voor dit gebied geldt dat de begrippen "eerder en later"
relatief zijn. Hier kan dat want deze punten en het punt "heden"
zijn ontkoppeld, het principe van "oorzaak en gevolg"
geldt hier niet.
 | Oefening 21
Maak een tekening waarin de lichtkegels van een buitenaards wezen op Venus,
van jou zelf en van een mannetje op Mars zijn weergegeven. De meest
suggestieve (en juiste) tekeningen worden opgenomen in de Website. |
Terug
Naar Uitleg §5 Optellen
|