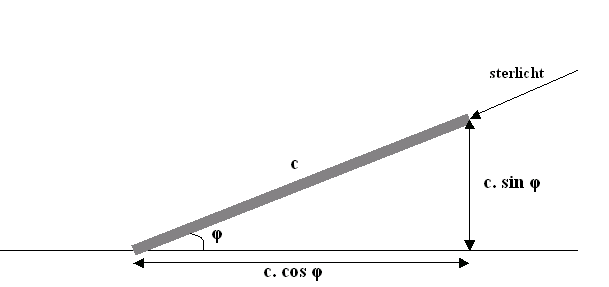
Figuur 1 Een ster wordt waargenomen onder de hoek φ
We stellen ons de sterrenkijker nu voor als een koker. Met
lenzen en spiegels willen we niets te maken hebben. De bundel licht
beweegt van voorpunt tot achterpunt door de koker.
We zullen laten zien dat een bewegende koker, met een waarnemer er
achter, onder een andere hoek φ'
naar de ster moet kijken en daarna laten we zien dat de frequentie van
het licht f ' een andere waarde aanneemt.
Het is niet verwonderlijk dat de koker onder een andere hoek op de
ster moet worden gericht, immers, vanwege de snelheid van de bewegende
koker komt het licht de koker tegemoet. De koker moet daardoor lager
worden gericht, zoals een fietser ook naar voren zal buigen als
hij door de loodrecht naar beneden vallende regen fietst om zijn
gezicht droog te houden.
We zijn geïnteresseerd in de hoek die de kijker moet innemen om het
licht langs de as van de koker te laten gaan. We nemen daarom een
bewegende koker waarvan de voorpunt precies even hoog boven de grond
steekt als de voorpunt van de stilstaande koker. Hun verticale
afmetingen zijn gelijk. De bewegende koker is dan iets langer dan de
stilstaande koker.
De afstand tot de ster is langs de bewegingsrichting gekrompen.
De ster staat daardoor iets hoger aan de hemel. De koker moet
dan iets meer omhoog worden gericht. Het effect van de snelheid v
op de richting blijkt echter veel groter te zijn dan het effect van de
gekrompen afstand waardoor de koker toch een minder grote hoek t.o.v.
de horizon inneemt. De hoekverandering door de snelheid gaat
zoals uit de formule blijkt met v/c terwijl de hoekverandering door de
afstandskrimp met (v/c)2 gaat. De sterrenkijker
verplaatst zich maximaal 2 mm als de kijker 20 meter lang is, omdat de
aarde een snelheid heeft van ongeveer 30 km/sec, terwijl de krimp als
gevolg van de contractie in de orde van 1/100 micrometer ligt. De
verandering van de hoek is dus heel klein en de lengtekrimp van de
bewegende lichtgrijze koker in de volgende figuren is verwaarloosbaar
klein.
In figuur 2 zien we de koker (in rust) terwijl een tweede
koker met een snelheid +v passeert. We nemen waar dat hij onder een hoek φ* op
de ster is gericht. In de tijd (1 sec in het stelsel in rust)
dat het licht zich van D naar E
beweegt door de rustende koker, verplaatst de bewegende koker zich over
een afstand v. De lichtstraal beweegt door de rustende koker,
maar als we ons de kokers doorzichtig denken, beweegt hetzelfde plukje
licht ook via de bewegende koker van D naar E. Probeer je
dat zo voor te stellen: terwijl de bewegende koker langs de stilstaande
schuift, beweegt het snijpunt van de twee kokers met de lichtsnelheid
langs de stilstaande koker. Het plukje licht bevindt zich voortdurend in
dat snijpunt. Het licht legt hierbij in de stilstaande koker een
afstand af van c meter en tegelijkertijd in de bewegende koker een
grotere afstand dan c meter. Het lijkt alsof
het licht in de bewegende koker sneller beweegt
dan de lichtsnelheid. Dit komt omdat de
bewegende koker tegelijkertijd langs het front
van de lichtgolf verschuift waardoor de bij D
binnenkomende lichtstraal in de bewegende koker
niet dezelfde is als de bij E
uittredende lichtstraal.
De hoek φ* verschilt een
heel klein beetje van de hoek φ'
die de waarnemer achter de bewegende koker zelf constateert omdat hij zijn
koker in de bewegingsrichting niet gekrompen ziet, hij beweegt namelijk niet
t.o.v de koker. Omdat wij ons op de bewegende aarde bevinden, willen wij de
hoek φ'
berekenen (zie figuur 3).
Voor de waarnemer bij de rustende koker is de hoek φ*
die de bewegende koker inneemt eenvoudig te bepalen uit de cosinus
van die hoek: aanliggende rechthoekszijde gedeeld door schuine zijde.
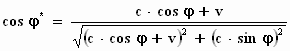
waarbij voor de schuine zijde Pythagoras is gebruikt.
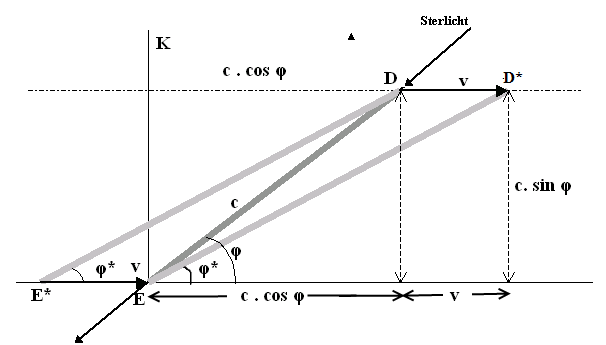
Figuur 2 Stilstaande koker ED wordt gepasseerd door de koker E*D die zich
na 1 sec op de plaats ED* bevindt
We bekijken dezelfde situatie vanuit het standpunt van de waarnemer
die zich bij de bewegende koker bevindt. Naar zijn oordeel houdt hij de
koker onder een hoek φ'
op de ster gericht. Zijn koker staat voor hem stil en hij wordt met een
snelheid – v gepasseerd door de eerst genoemde koker van figuur 1.
Dit is te zien in figuur 3. De hoek die de passerende koker
volgens hem inneemt is φ**.
Deze hoek φ** zullen we niet
behoeven uit te zoeken, want wij kunnen volstaan met het vinden van de hoek φ'
. De hoek φ' is de hoek waarmee sterrenkundigen te maken hebben. De
waarde van φ** staat echter tevoren vast: φ** = φ !!
Waarom? Omdat je weer terug bent op je uitgangspunt.
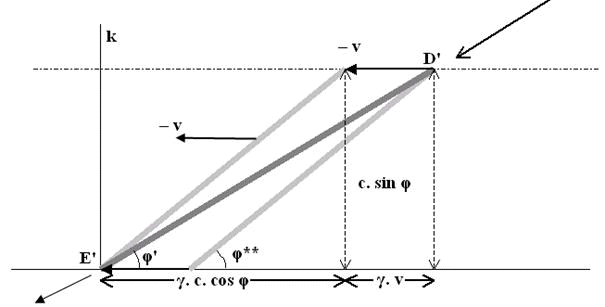
Figuur 3 Gezien vanaf de bewegende koker passeert de rustende koker met
een snelheid – v.
We beredeneren de hoek φ'
. Vanuit het eerste, rustende stelsel zagen we de bewegende koker
passeren onder een hoek φ*.
De hoogte van de gevormde driehoek was c . sin φ en
de aanliggende rechthoekszijde was c . cos φ
+ v. De hoogte in de y–richting verandert niet als je van
stelsel verwisselt, maar de lengte van de aanliggende rechthoekszijde
verandert wél. De afstand c . cos φ + v
is de horizontale component van de passerende koker D'E'
zoals gezien vanuit het rustende stelsel. De waarnemer bij de bewegende
koker zal een γ keer
grotere lengte opmeten voor deze rechthoekszijde. Volgens hem is die
lengte γ . (c . cos φ + v).
Ook de lengte van de koker zelf krijgt daarmee een andere waarde,
namelijk:
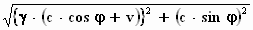
Hiermee kunnen we cos φ'
berekenen:
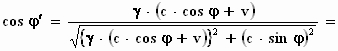
We halen γ onder het
wortelteken vandaan:
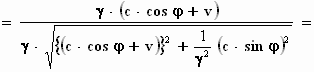
We delen vervolgens de teller en noemer door γ
en schrijven het kwadraat 1/γ2
onder het wortelteken uit.
Bedenk
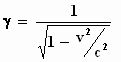 dus:
dus:
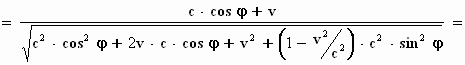
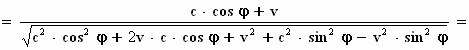
We pakken nu c2. cos2 φ
+ c2. sin2 φ
samen tot c2 en voor v2 .
sin2 φ
schrijven we
v2 . sin2 φ
= v2 . (1–cos2
φ ):
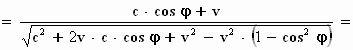
Nu valt v2 weg tegen – v2:
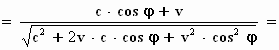
Onder het wortelteken blijkt nu een kwadraat te staan: (c + v.
cos φ)2
.
Daarmee krijgen we als resultaat:
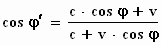 of
of
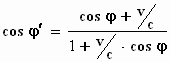
Naar deze formule waren we op zoek! Hij wijkt een beetje af van de
formule in het artikel van Einstein omdat we de snelheid van de
waarnemer positief hebben genomen als hij de bron nadert, terwijl in de
afleiding van Einstein de snelheid positief is als de bron zich van de
waarnemer verwijdert.
(Eigenlijk bevalt deze formule mij beter dan die van Einstein, voor
een snelheid + v naar de lichtbron toe staat in de hier
afgeleide formule ook een +teken)
Overigens, als we eenmaal weten dat de verandering van de hoek
waaronder de ster wordt bekeken vooral afhangt van de snelheid waarmee
de kijker beweegt ten opzichte van de ster en dat de kokerkrimp kan
worden verwaarloosd, dan kunnen we uit de formule:
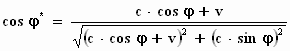
zeer snel de uiteindelijke
formule afleiden, want:
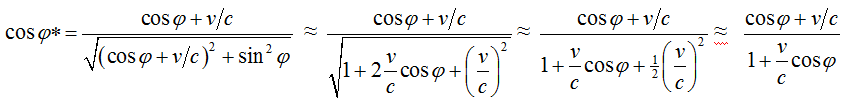
De omweg via figuur 2 is eigenlijk niet nodig, maar dat is
achterafgepraat.
Wie zich afvraagt waar nu het relativistische aspect in dit verhaal is
gebleven: dat is de aanname dat de lichtsnelheid gelijk is aan c,
er wordt niet gecorrigeerd voor de tijdvertraging of de
Lorentzcontractie omdat deze effecten te verwaarlozen zijn.
De Relativistische DOPPLERVERSCHUIVING!
Nu de kwestie van de frequentie in het stelsel–in–beweging.
We bekijken het vanuit het stelsel–in–rust. De stilstaande koker
strekt zich uit van D
tot E. Op het tijdstip t = 0 valt het voorste punt van de
passerende koker samen met het punt D. Op het tijdstip t = 1
valt het achterste punt van de passerende koker samen met het punt E.
De frequentie in het stelsel–in–rust is f. Dus in die éne
seconde zijn er f golfjes met de golflengte λ
de rustende kijker binnengetreden en ze komen precies op dat moment bij E
er weer uit. In diezelfde tijd is het aantal golfjes dat de bewegende
koker binnenging groter, want de koker heeft zich in de richting van de
bron verplaatst. Uit figuur 4 is te zien dat het aantal golfjes
dat zich in het gebied v . cos φ
voor D
bevindt ook de koker is ingegaan. Dat aantal is (v. cos φ)/
λ .
Dus vanuit het stelsel–in–rust zie je in 1 sec een aantal
van f
+ (v. cos φ)/ λ golfjes de
koker in verdwijnen.
De tijd in het stelsel–in–beweging tikt echter trager. Wat in het
stelsel–in–rust
1 sec duurt, duurt in het stelsel–in–beweging 1/γ
sec. Daarom wordt de frequentie in het stelsel–in–beweging
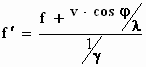
Bedenk dat λ = c/f
en
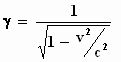 Daarmee wordt:
Daarmee wordt:
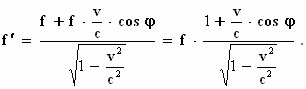
Ook in deze formule is - v t.o.v.
de formule van
Einstein door +v vervangen.
We vinden hier de formules van Einstein voor de
Dopplerverschuiving en de aberratie van het sterlicht
gevonden zonder van de
Maxwellvergelijkingen gebruik te maken!
Einstein zei direct in het begin van zijn artikel dat iedere theorie
over de elektrodynamica uit moet gaan van de bewegingsleer van
onvervormbare voorwerpen omdat daarmee uitspraken over de relatie tussen
de voorwerpen, klokken en elektromagnetische processen kunnen worden
gedaan. Dat hebben we hier aardig in de praktijk gebracht met onze
starre kokers.
Het vinden van het juiste pad voor deze afleiding was
een hels karwei. Het goed uit elkaar houden van de twee stelsels en het
bedenken in welk stelsel je zelf zit, blijft uitermate verwarrend. Uw gids
is dan ook zeer tevreden u deze praktische en uiteindelijk heldere,
voorbeelden voor te kunnen leggen.
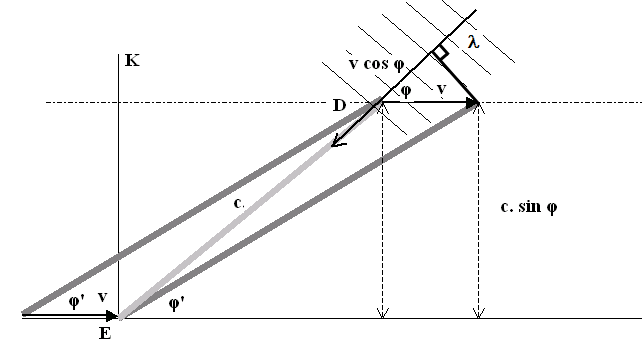
Figuur 4 De bewegende koker slokt nog wat extra golfjes op
Terug
|