|
|
§7 Verkleurende en verschuivende
sterren
Naar Uitleg §7
Plus Afleidingen
Naar Uitleg §8 Lichtenergie en -druk
Naar Uitleg §6 Maxwell
Naar Uitleg Inhoud
Naar Vertaling §7 Doppler en aberratie
Naar Centrale Hal
Aan het eind van de negentiende eeuw lag men niet wakker over het
Dopplereffect voor licht. De verklaring zoals deze gold voor geluid zou ook wel
kloppen voor licht. Wie daar echter geen genoegen mee nam was Hendrik Antoon
Lorentz die in zijn "Versuch einer Theorie" (een
"bijna–relativiteitstheorie") naar de stand van
de wetenschap van dat moment (1895) de ultieme theorie over
elektromagnetische verschijnselen en dus ook over licht publiceerde. Ook het Dopplereffect kreeg daarin
een plaats. Er was geen speld tussen te krijgen ondanks de bescheiden titel van
de publicatie.
Iedereen tevreden: weer een stukje natuurkunde af!
Maar als Einstein hetzelfde verschijnsel onder het mes van de
relativiteittheorie legt, ontstaan er andere formules en wordt de fysische
interpretatie beslist anders dan die voor geluid.
Eerst even het geheugen opfrissen:
Het Dopplereffect
 |
Christian Johann Doppler (1803–1853) Oostenrijks wiskundige uit Saltzburg.
Ontdekte in 1842 voor geluiden dat de toon de hoogte in ging bij nadering en
omlaag ging bij verwijdering van de bron. Armand Fizeau suggereerde in 1848
dat het Dopplereffect bij licht tot een blauwverschuiving of een
roodverschuiving leidt. Goed gezien! Einstein heeft het in de hier
besproken publicatie consequent over het "Doppeler"
effect, hij mocht de man misschien niet! |
Voor geluid
Het Dopplereffect kennen we allemaal voor het geluid van een snel passerend
voertuig of overvliegend vliegtuig. Bij nadering is het geluid hoger dan
wanneer het vervoermiddel zich weer verwijdert. Het meest opvallende voorbeeld
is misschien wel de alarmbel die we kunnen horen bij een onbewaakte overweg
(zolang deze nog bestaan) wanneer we in een trein zitten. Dan zijn we zelf in
beweging ten opzichte van de bel, maar het verschijnsel doet zich dan evengoed
voor. Ook dit geluid verloopt van hoog naar laag.
De verklaring is niet moeilijk. Het geluid heeft een constante snelheid ten
opzichte van de lucht. We geven de geluidsnelheid, net als de lichtsnelheid,
ook met het symbool c aan. Dit kunnen we wel even uit elkaar houden, denk ik.
Dus c meter per seconde.
We gaan uit van stilstaande lucht. De geluidbron heeft een frequentie van f
hertz(Hz). Dus f trillingen per seconde. Als de geluidbron en de waarnemer stilstaan ten opzichte van elkaar bevinden
zich in een afstand van c meter dus f trillingen.
Wanneer de bron zich met een snelheid + v m/s van de waarnemer verwijdert,
moeten diezelfde f trillingen per seconde zich in een gebied met een lengte van
(c + v)
meter bevinden, immers de eerste, uitgezonden trilling die we in ogenschouw
nemen heeft zich na één
seconde c meter verwijderd van het punt waar hij werd uitgezonden (en bereikt
de waarnemer) en de laatste trilling, die in de betreffende tijdsduur
van één seconde wordt
uitgezonden, ontsnapt aan de bron op een plaats die v meter verder weg ligt
van de waarnemer. De f trillingen die de waarnemer in de betreffende seconde passeren, liggen dus verder
uiteen. Ze nemen een afstand van (c + v) meter in. De golflengte is langer geworden.
De frequentie die de waarnemer hoort is:
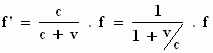
Wanneer de bron de waarnemer nadert, verandert het teken van
de snelheid. In de noemer komt dan een minteken te staan in de plaats van het
plusteken. De formule blijft hetzelfde.
Maar als de waarnemer zich verplaatst terwijl de bron stil blijft
staan, krijg je een andere situatie. Als de waarnemer zich met een snelheid
van + v m/s van de bron verwijdert, terwijl de bron stilstaat, wordt de
waarnemer in één seconde door minder dan f trillingen ingehaald. Het gaat
nu om de geluidtrillingen die zich in een gebied van (c
– v) meter bevinden.
Dat zijn er (c – v)/c keer zo weinig als bij stilstand.
De frequentie die de waarnemer nu hoort, is:
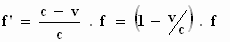
Er zijn dus twee formules, één voor de bewegende bron en één voor de
bewegende waarnemer. Dat er twee formules moeten zijn, wordt duidelijk als je
je voorstelt dat de bron zich met de geluidsnelheid verwijdert: dan wordt
hetzelfde aantal trillingen per seconde over een tweemaal zo grote afstand
uitgesmeerd, dus de frequentie wordt de helft. Als daarentegen de waarnemer
zich met de geluidsnelheid van de bron verwijdert, kunnen de geluidgolven de
waarnemer niet meer inhalen: de frequentie wordt nul!
Als v veel kleiner is
dan c leiden beide formules tot praktisch dezelfde uitkomst.
Als laatste kunnen we ons nog afvragen hoe de formules er uit
gaan zien als de richting van v een hoek φ
maakt met de voortplantingsrichting van het geluid. Dan
moeten we de component van v nemen in de bewegingsrichting van het
geluid: v . cos φ en daarmee
krijgen we de volgende formules:
Bewegende geluidbron:
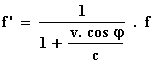
Bewegende waarnemer:
|
|
Voor licht
Iedereen, ook Lorentz, ging er van uit dat het Dopplereffect voor licht, dat
zich volgens de opvattingen in die tijd door de stilstaande
"lichtether" voortbewoog met een constante snelheid c ten
opzichte van de "lichtether", op dezelfde wijze als door de twee
formules voor geluid in stilstaande lucht diende te worden beschreven.
Einstein schudde hen wakker en kwam voor het Dopplereffect voor licht tot één
formule, waarbij het niet uitmaakt of de bron of de waarnemer beweegt! Echt een
stukje relativiteit!
We zullen zijn redenatie volgen. Ga er maar even rustig voor zitten, maar houd
je goed vast. Gewoon door de transformatieformules toe te passen, wist Einstein
tot dan toe onverklaarde effecten op te helderen. Niet alleen het Dopplereffect,
maar ook de aberratie, de rood- en blauw verschuiving en de
intensiteitverandering . Let maar op.
 |
Wie echter opziet tegen Maxwellvergelijkingen en het
gemanipuleer daarvan via de Lorentztransformaties kan terecht bij de
alternatieve afleiding van de formules zonder
Maxwellvergelijkingen: Begrijpelijke afleidingen |
In het stelsel-in-rust K bevindt zich ver van de oorsprong in
het punt (x, y, z ) een bron die elektromagnetische golven uitzendt. We
zullen de elektromagnetische golven met regelmaat ook gewoon "licht"
noemen. Het punt wordt voor het gemak zeer ver van de oorsprong genomen zodat de
waargenomen golven constant in grootte en richting zijn, zowel voor een
waarnemer in het stelsel–in–rust als voor een bewegende waarnemer die een
beetje in de buurt blijft.
De lichtgolven bereiken de waarnemer. Als deze zich in de
oorsprong van het stelsel–in–rust K bevindt, kunnen we de componenten
voor het elektrisch veld en voor het magnetisch veld van het licht opschrijven:
X = X0 . sin Φ,
L = L0
. sin Φ,
Y = Y0 . sin Φ,
M = M0
. sin Φ,
Z = Z0 . sin Φ,
N = N0
. sin Φ,
Dit is een algemene manier van beschrijven van de sterkte van de golf op
een bepaalde plaats. De sterkte van de
componenten X, Y en Z van elektrische vector tonen een sinus-vormig verloop,
evenals de componenten L, M en N van de magnetische vector. Je zal
hierin, als je het onderwerp trillingen wel eens hebt gehad, de formule A.sin2 πft
herkennen, waarbij A de amplitudo is, f de frequentie en t de tijd vanaf het
moment dat de golf begon. De hoek Φ
= 2πft wordt in radialen uitgedrukt. De
formule kan ook worden geschreven als A . sin ω t , waarbij ω
de hoekfrequentie of hoeksnelheid in radialen/s wordt genoemd.
Vanzelfsprekend geldt dan de vergelijking ω = 2πf of (omdat f = 1/
T ) geldt ook ω = 2π/T, waarbij T de trillingstijd is. Het omrekenen van een
hoek in graden of in radialen is altijd gemakkelijk te doen als je bedenkt
dat het doorlopen van een hele cirkel neerkomt op 360 ° of 2π radialen.
Alle componenten van het elektrische en het magnetische veld variëren, zoals
gezegd, met de
tijd sinusvormig in sterkte. De variatie gaat in dit geval synchroon. Alle componenten
bereiken tegelijkertijd de maximale waarde (de amplitudo), gaan tegelijkertijd
door nul en bereiken vervolgens de uiterste waarde in negatieve zin. Je hebt
hier te maken met lineair gepolariseerd licht, dat het eenvoudigst te
beschrijven is. We maken het niet moeilijker dan het al is.
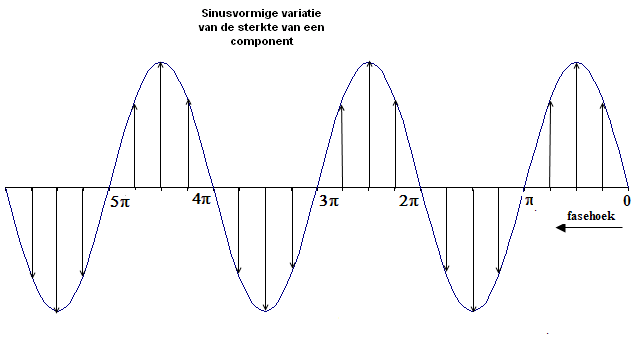
Figuur 7. 01 Iedere component van het elektrisch veld en ook van het
magnetisch veld varieert op de wijze zoals in de figuur is aangegeven
Wanneer we de eerste vergelijking onder de loep nemen, X = X0 .
sin Φ, dan is X0
daarin de amplitudo van de x–component van het elektrische veld en Φ
is een hoek in radialen, die evenredig met de tijd toeneemt. De hoek Φ
wordt de fasehoek genoemd. Als Φ
de waarde π/2 heeft, is sin Φ
= 1 en bereikt de component zijn maximale waarde, de amplitudo.De
hoek π/2 komt overeen met 90
º. Voor Φ = 0, π
of 2π heeft sin Φ
de waarde 0 en voor Φ = 3π/2
wordt sin Φ = – 1. Dit
herhaalt zich elke trilling. De hoek Φ
wordt ook wel de fasehoek genoemd. De hoek loopt na 2π
gewoon door. Bij Φ = 4π
zijn er twee trillingen doorlopen, enzovoort (zie figuur 701).
Wanneer de bron t seconde bezig is met golven uitzenden, dan is de
doorlopen fasehoek van de trilling bij de bron zelf: Φ
= ω . t radialen. Op een afstand s van de bron is de
fasehoek van de golf die daar op dat tijdstip t passeert: Φ
= ω . (t – s / c), want de golven komen daar pas s/c
seconde, nadat ze de bron verlaten hebben, aan.
De afstand s tussen de bron en de oorsprong van het stelsel-in-rust
geeft Einstein aan met
s = a.x + b.y + d.z
waarbij x, y en z de componenten van s langs de drie
assen zijn en waarbij a, b en d de richtingscosinussen van de
afstand worden genoemd. In figuur 702 is de afstand s aangegeven. De
componenten van s worden verkregen door s op elk van de drie assen
te projecteren. Een handige, maar in onbruik geraakte methode.
Voor x geldt x = s . cos α.
De richtingscosinus a is gelijk aan cos α
, die weer eenvoudigweg gelijk is aan x / s.
Voor y geldt y = s . cos β met
de richtingscosinus b = cos β = y
/ s
en voor z geldt z = s . cos γ
met de richtingscosinus d = cos γ = z / s.
Hiermee wordt a.x + b.y + d.z = x2 / s + y2 / s + z2
/ s
= (x2 + y2 + z2) / s = s2 / s =
s.
Bedenk dat de stelling van Pythagoras in de ruimte luidt: x2 +
y2 + z2 = s2.
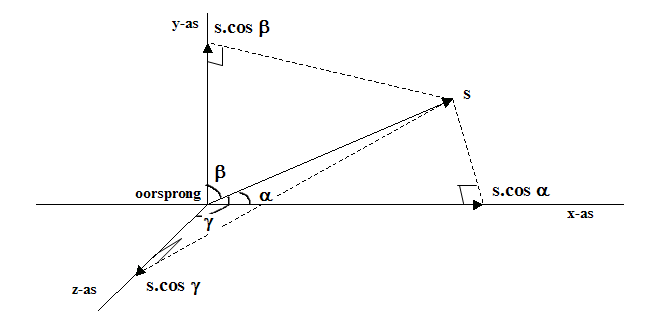
Figuur 702 De richtingscosinussen
Op deze manier is de afstand s direct in zijn componenten a.x, b.y
en d.z weergegeven.
De fasehoek Φ wordt hiermee:
Φ
= ω . 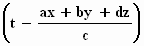 . .
De tijd t
hoort bij het punt (x, y, z) waar de bron zich bevindt.
De tijdsduur t* = (ax+by+dz)/c is de tijd die de golf
er over heeft gedaan om vanaf de bron de stilstaande waarnemer in de oorsprong
te bereiken .
De uitdrukking tussen haken: 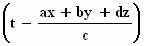 is gelijk aan (t – t*) , dat is de tijdsduur dat de waarnemer in de
oorsprong de golven reeds waarneemt.
is gelijk aan (t – t*) , dat is de tijdsduur dat de waarnemer in de
oorsprong de golven reeds waarneemt.
Einstein schrijft de fasehoek op bovenstaande wijze op omdat je er dan vat op
hebt, je kunt hem transformeren. De variabelen die er in voorkomen t, x, y en z kunnen namelijk worden
getransformeerd met de transformatieformules. Voor de veldcomponenten X, Y, Z
en L, M en N zijn de getransformeerde formules ook bekend. Het is nu de bedoeling uit te zoeken
welke grootte een waarnemer in een bewegend stelsel (ten opzichte van het
stelsel-in-rust en de bron)
aan de zes componenten van het elektromagnetische veld zal toekennen (zie figuur
703).
Als Φ' de fasehoek is die de
bewegende waarnemer constateert, kan hij daarvoor opschrijven:
Φ ' = ω ' . 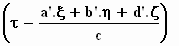 , ,
waarbij op het tijdstip τ* = (a' . ξ +
b' .
η + d' . ζ) / c de golf de waarnemer in het stelsel-in-beweging
bereikt.
De waarnemer in het stelsel-in-beweging zal volgens de getransformeerde
formules van de vorige paragraaf de zes componenten zien als:
X ' = X =
X0 . sin Φ ',
L ' = L = L0
. sin Φ ',
Y ' = γ . (Y0 – 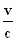 .N0)
. sin Φ ',
M ' = γ . (M0
+ .N0)
. sin Φ ',
M ' = γ . (M0
+ 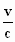 .Z0
). sin Φ ', .Z0
). sin Φ ',
Z ' = γ . (Z0 + 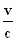 .
M0) . sin Φ ',
N ' = γ . (N0
– .
M0) . sin Φ ',
N ' = γ . (N0
– 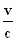 .Y0)
. sin Φ ', .Y0)
. sin Φ ',
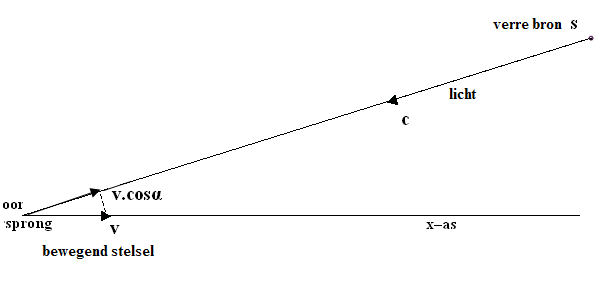
Figuur 703 De waarnemers in het stelsel–in–beweging komen dichter bij de
bron
Nu is het aardige dat de fasehoek Φ ' =
ω ' . 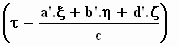 de getransformeerde functie moet zijn van Φ
en beide functies moeten dezelfde vorm hebben , immers volgens het
relativiteitsprincipe geldt: "De natuurkundige
wetten zijn onafhankelijk van het stelsel". Bovendien moeten
Φ en Φ'
ook nog dezelfde waarde hebben
de getransformeerde functie moet zijn van Φ
en beide functies moeten dezelfde vorm hebben , immers volgens het
relativiteitsprincipe geldt: "De natuurkundige
wetten zijn onafhankelijk van het stelsel". Bovendien moeten
Φ en Φ'
ook nog dezelfde waarde hebben
Om daar meer over te weten te
komen, transformeren we het ding gewoon terug met:
τ = γ (t – 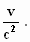 x)
ξ
= γ (x – v.t) η = y
ζ = z x)
ξ
= γ (x – v.t) η = y
ζ = z
Dan krijgen we:
Φ' = ω' 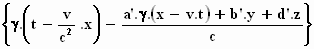
Om te zien of dit van dezelfde vorm is, moet je hem zo herschrijven dat hij
zoveel mogelijk lijkt op
Φ = ω . 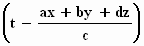 . .
Dat valt niet mee, maar na wat gepriegel en gehannes, krijg je:
Φ ' = 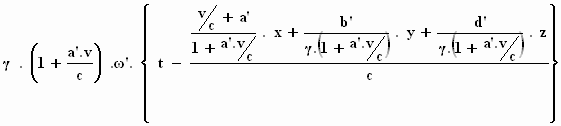
Als je de uitdrukkingen voor Φ
en voor Φ' vergelijkt, kom je
tot de conclusie dat de vorm dezelfde is als de volgende gelijkheden gelden:
ω = γ . 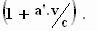 ω'
; ω'
;
a = 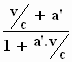 ; ;
b = 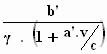 ; ;
d = 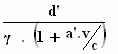
Deze gelijkheden moeten dus gelden omdat volgens het
relativiteitsprincipe de vorm dezelfde moet zijn!! Dit is de hogere
filosofie achter de theorie. Als die aanname niet klopt, valt alles in
duigen, maar tot op heden is de aanname rechtovereind gebleven.
In één moeite door zal nu ook Φ
gelijk zijn aan Φ'.
Met behulp van de gelijkheden kan je a', b', d' en ω'
in a, b, d en ω
uitdrukken. Dat gaan we doen, om te beginnen met a', want a' heb
je in de drie ander formules ook nodig. In één van de bovenstaande formules
staat a uitgedrukt in a'. Je kan a en a' met
elkaar verwisselen en v verwisselen met - v. Dan krijg je
het volgende resultaat, maar je kan a' ook uit de vergelijking oplossen.
Dat kost wat meer tijd en je
maakt makkelijk vergissingen, maar je krijgt ook:
a ' = 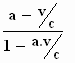
In de drie andere formules komt de uitdrukking γ
.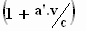 voor. voor.
Als we hierin a ' invullen en ons herinneren dat voor γ
geldt: γ = 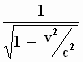 ,
dan blijkt: ,
dan blijkt:
γ .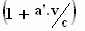 = =
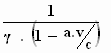 . .
Hiermee kom je eenvoudig op:
b ' = 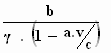 ; d ' =
; d ' =
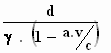 ;
; ω'
= 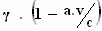 . ω
. ω
Deze uitdrukkingen staan in het artikel van Einstein halverwege blz. 911.
De uitdrukking voor ω' leidt ons
nu direct naar het Dopplereffect voor elektromagnetische straling in het
algemeen en licht in het bijzonder. Let maar op:
Wegens de relatie ω = 2π . f
tussen de hoekfrequentie ω en de
gewone frequentie f en
ω' = 2π . f ' geldt dus dat de waarnemer in het stelsel-in-beweging
een frequentie f ' constateert die gelijk is aan:
f ' = 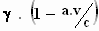 . f
. f
waarbij f de frequentie is die een waarnemer in het stelsel-in-rust
constateert en waarbij
a = cos α
= x / s.
Verder geldt nog altijd γ > 1.
Let op: de bewegingsrichting van het stelsel-in-beweging en van het licht
dat de waarnemers tegemoetkomt is in figuur 703 tegengesteld, zodat v/c in
die situatie negatief is! Dan is f ' groter dan f .
We gaan het probleem vereenvoudigen. Als we de bron in het xy–vlak kiezen,
zijn er van de drie
mogelijke hoeken α, β en γ
nog maar twee over, α en β
, waarbij geldt β =
90o - α. Eigenlijk is er
nu nog maar één onafhankelijke hoek over.
 | We kiezen de hoek met de x-as
en we noemen die hoek φ. |
De richtingscosinus a is dan de cosinus van de hoek φ
tussen de lichtstralen van de bron en de x–as van het stilstaande
stelsel: a = cos φ .
Bedenk dat de x–as samenvalt met de ξ–as van het bewegende
stelsel dat zich in de richting van de positieve x–as beweegt.
Dopplereffect en rood- en blauwverkleuring
Als we nu a en γ
uitschrijven, krijgen we het "relativistische" Dopplereffect:
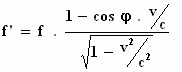
Bekijk ook eens de alternatieve afleiding van deze
formule zonder gebruik van de Maxwellvergelijkingen: Begrijpelijke afleidingen
Vergelijk dit resultaat met de klassieke formules in het begin en je ziet dat
waar er voor geluid een onderscheid wordt gemaakt tussen de bewegende bron en de
bewegende waarnemer, voor elektromagnetische golven (licht) slechts één
formule nodig is waarbij alleen de relatieve beweging tussen waarnemer en bron van
belang is.
Hier keken Einsteins tijdgenoten behoorlijk van op!
In de teller van de formule staat het resultaat dat bij geluid voor een
bewegende waarnemer wordt gevonden. Het is de vraag waarom de bewegende
bron niet meedoet, dat moeten we nog eens uitzoeken. In de noemer staat uitsluitend het
effect van de snelheid op de tijd.
Vervolgens laat Einstein zien wat er gebeurt als de waarnemer zich beweegt
langs de lijn waarnemer –––– bron, de zichtlijn. De hoek φ
is dan nul. Je krijgt:
f ' = f . 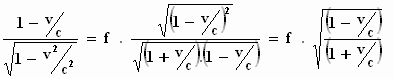
Dit kan ook worden geschreven als f '. 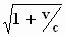 =
f . =
f . 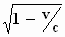 , waarmee de symmetrie tussen het
stelsel–in–beweging en het stelsel–in–rust mooi tot uitdrukking komt. , waarmee de symmetrie tussen het
stelsel–in–beweging en het stelsel–in–rust mooi tot uitdrukking komt.
Als v/c positief wordt genomen verwijderen de bron en de
waarnemer in het stelsel-in-beweging zich van elkaar. Dan is f ' < f, de
situatie van roodverschuiving. Als v/c negatief is, naderen de
bron en de waarnemer elkaar. Dan wordt het blauwverschuiving. Als de
snelheid v is, dan is de verschuiving voor alle frequenties eenzelfde
factor. Daarom hoeft een sterrenkundige maar van één spectraallijn te
weten hoeveel deze in frequentie is verschoven om de snelheid van de bron te
kennen.
Vraag:
Een emissielijn van het element zuurstof heeft een golflengte van
0,3727 µm als je de golflengte in het laboratorium meet. In een ver
verwijderd sterrenstelsel wordt deze lijn ook aangetroffen maar de hier
gemeten golflengte is als gevolg van de roodverschuiving 0,415
µm. Bereken met welke snelheid het sterrenstelsel zich van ons verwijderd.
Gebruik voor de lichtsnelheid c = 2,998 x 108 m/s.
(Antw. 32,1 x 106 m/s)
Hier wijst Einstein er in de originele tekst p.912 op dat als v = – ∞
dat dan f = ∞.
Dat moet een typefout zijn want oneindige snelheden zijn onbestaanbaar volgens
Einstein zelf. We nemen de vrijheid te veronderstellen dat bedoeld is: v = + c,
zodat v/c = –1 en f ' =
∞.
Dan wordt de noemer 0 en de frequentie f ' wordt oneindig. "In
tegenstelling tot de gebruikelijke opvatting", zegt Einstein. Volgens de
gebruikelijke opvatting werd een dubbele frequentie f ' = 2.f verwacht.
We kunnen er aan toevoegen dat als de waarnemer zich met de lichtsnelheid
verwijdert van de bron de "waargenomen" frequentie nul wordt, net als
wanneer een waarnemer zich met de geluidsnelheid van een geluidbron zou
verwijderen. Daarin zit geen onverwachte uitkomst.
|
|
Terug
Aberratie
Uit de afgeleide formules geeft Einstein vervolgens een nieuwe verklaring
voor een al lang bekend verschijnsel dat het gevolg is van de snelheid van de
aarde in zijn baan rond de zon. De snelheid van de aarde ten opzichte van de
sterren vertoont een jaarlijkse variatie. Als gevolg hiervan vertonen de
posities van de sterren op de hemelbol ook een jaarlijkse variatie. Het
verschijnsel wordt aberratie genoemd of met een oude term:
"afdwaling van het licht".
 | zie Hub. J. Bouten "Nieuw Leerboek der Cosmographie (1906) p.61 |
Alle sterren doen er in dezelfde mate aan mee.
Het moet wel worden onderscheiden van de verschuiving van plaats voor
dichtbij staande sterren ten opzichte van ver weg gelegen sterren als gevolg
van onze jaarlijkse beweging, de jaarlijkse parallax. Met een oude term:
"Jaarlijksch verschilzicht der vaste sterren". De aberratie komt door
de snelheid van de aarde, de parallax komt door de verplaatsing van de
aarde. De parallax is alleen waarneembaar voor nabije sterren.
De klassieke verklaring voor de aberratie is door de ontdekker van het
verschijnsel, Bradley , al in 1729 gegeven (zie figuur 704).
 |
James Bradley 1693-1762 Brits Astronoom, geboren in Sherborne, doceerde aan
de universiteit van Oxford. Befaamd om zijn nauwkeurige metingen. |
Het is dezelfde verklaring die ook wordt gegeven voor de richting waarmee de
regen tegen een fietsende fietser aanklettert als de regen loodrecht naar
beneden valt (voor een stilstaande waarnemer). Voor de fietser valt de regen
niet loodrecht naar beneden, als hij hard genoeg fietst krijgt hij de regen in
zijn gezicht. Hij zal iets naar voren buigen zodat de regen alleen op zijn kop
terecht komt.
Bradley constateerde dat een bepaalde vaste ster (de twee na helderste uit het
sterrenbeeld de Draak), die hij een groot deel van het jaar iedere nacht in zijn
sterrenkijker in het vizier kreeg in de loop der tijd van
positie veranderde. Het was een goed meetbaar effect, waarvan hij ontdekte dat
het niet de jaarlijkse parallax kon zijn. Hij bracht het effect in verband met
de eindige lichtsnelheid en de snelheid van de aarde in zijn baan om de zon.
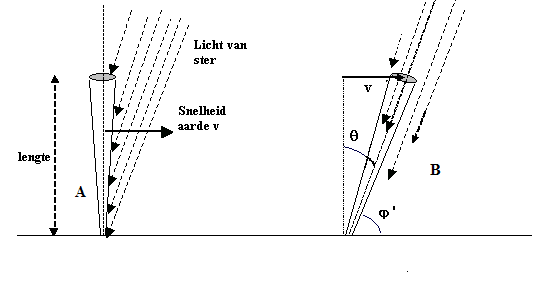
Figuur 704 Door de aardbeweging moet een kijker iets worden gekanteld
De redenatie is de volgende: de tijd t die het licht van de
ster er over doet om van de objectieflens (vooraan) van een sterrenkijker tot
aan het oculair (ooglens) te komen, is t = ℓ/c.
Hierin is ℓ de lengte van de kijker. In die tijd heeft de
sterrenkijker zich over een afstand v.t = v.ℓ/c verplaatst omdat
hij meebeweegt met de aarde. Om het beeld van de ster toch in het midden van het
oculair te krijgen moet de kijker enigszins worden gekanteld. Die kantelhoek
wordt gevonden met
sinus θ = 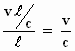
Het quotiënt v/c wordt de aberratieconstante genoemd. Dit is
de maximale afwijking, want naarmate het sterlicht minder loodrecht invalt,
wordt de afwijking kleiner. Jaarlijks wordt door iedere vaste ster op die manier
een ellips beschreven tegen de hemelbol met een lange as van 41 boogseconden.
Daarbij geldt: als we een ster tegemoet snellen, staat hij schijnbaar lager en
als we ons van de ster verwijderen staat hij schijnbaar hoger. Tweemaal per jaar
heeft een ster zijn grootste hoekafwijking ten opzichte van zijn gemiddelde
plek, namelijk als het aankomende sterlicht en de snelheid van de aarde
loodrecht op elkaar staan. Op die momenten kom je de
ster niet tegemoet en je verwijdert je er evenmin van.
Je zou verwachten dat de aberratie het grootst is als
je zo snel mogelijk in de richting van de ster of er
vandaan beweegt, maar nee!
In figuur 705 zijn dat de plaatsen 1 en
2.
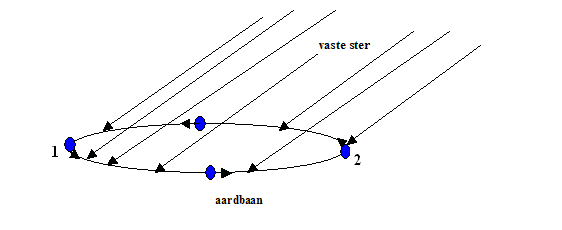
Figuur 705 Tweemaal per jaar staat de snelheid van de aarde loodrecht op het
invallende licht van een vaste ster
 |
Boogseconde: De grootte van een hoek
wordt uitgedrukt in graden. Een rechte hoek is 90o. Kleine hoeken
of onderdelen van een hoek kunnen decimaal worden aangegeven, bijvoorbeeld
7,4438o , maar gebruikelijk is om kleine hoeken uit te
drukken in minuten en seconden. Een boogminuut is één zestigste graad en
een boogseconde is één zestigste van een boogminuut. Zo wordt de genoemde
hoek 7 graden 26 minuten 37,68 seconden. Je ziet, uiteindelijk verval je
toch weer in het decimale systeem. |
 | Vraag: Als een sterrenkijker een lengte heeft van 12 m,
bereken dan de tijd die het licht er over doet om van objectieflens tot het
oculair te geraken. Over welke afstand heeft de kijker zich in die tijd
verplaatst? Laat zien dat bij een lichtinval die loodrecht staat op de
bewegingsrichting van de aarde de hoek thêta θ
gelijk wordt aan 20,4 boogseconde.
Gebruik c = 2,998 x 108
m/s en de aardsnelheid is v = 29,7 x 103 m/s.
(Antw: 40,0 x 10-9 s en 1,19 mm) |
In de tweede helft van de negentiende eeuw, dus na 1850, kwam deze verklaring
steeds meer onder vuur te liggen. Als de kantelhoek namelijk afhing van de tijd
die het licht er over deed om van de objectieflens tot het oculair te komen, dan
zou de kantelhoek moeten veranderen als je de kijker zou vullen met een
materiaal waarin het licht een lagere snelheid had. Zo'n materiaal is water.
Daarin is de lichtsnelheid ongeveer 75 % van die in lucht. De kantelhoek zou
1,33 maal zo groot moeten zijn. De Engelsman Airy waagde er in 1871 zijn
telescoop aan en vulde hem spontaan met water. Na een grondig onderzoek kwam hij
met een verrassend resultaat: de kantelhoek was niet veranderd!! Dus de
verklaring van Bradley klopte niet.
 |
George Biddell Airy, Brits sterrenkundige, geboren in Alnwick (1801),
hoogleraar aan de universiteit van Cambridge, vooral bekend omdat hij het
belang van de veldtheorie van Michael Faraday niet onderkende en John Adams
ontdekking van de planeet Neptunus in 1845 niet geloofde. Ook in dit geval
wist hij iets niet aan te tonen, maar hij had wel gelijk. Overleden in 1892. |
In zijn "Versuch einer Theorie" blz. 88 weet onze wegbereider van
de Relativiteitstheorie, H.A.Lorentz, het negatieve resultaat van Airy op een
moeizame wijze te verklaren.
Einstein echter scherpt op heldere wijze in enkele bladzijden de formule nog wat
aan en bevestigt dat het medium er niet toe doet. Hij laat zien dat de aberratie
eenvoudig te vinden is uit het verschil van de richtingscosinus φ
van de bron in
het stelsel-in-rust en de bewegingsrichting van het stelsel-in-beweging.
Neem de formule a ' = 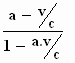 ,
van een stukje terug. ,
van een stukje terug.
Als je de betekenis van a en a' invult, staat er:
cos φ'
=
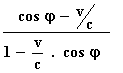
Deze uitdrukking bevat beide richtingscosinussen van het sterlicht ten opzichte
van de sterrenkijker op aarde. Voor een stilstaande aarde zou gelden cos φ
en voor de bewegende aarde geldt: cos φ'.
De hoek φ
is de hoek tussen de richting naar de ster
en de richting waarin de aarde beweegt. In de loop van
het jaar verandert de hoek φ.
De aberratie is het verschil tussen φ en φ'.
 | Bekijk ook eens de alternatieve afleiding van deze
formule zonder gebruik van de Maxwellvergelijkingen: Begrijpelijke afleidingen.
Let op: achteraf blijkt dat de hele
berekening veel eenvoudiger kan omdat de
tijdvertraging en de Lorentzcontractie geen
rol spelen. Het enige dat uit de
relativiteitstheorie meespeelt, is de
constante lichtsnelheid. |
Deze formule geeft het verschijnsel aberratie in de meest algemene vorm weer, zo
stelt hij. Als φ = π / 2,
dus cos φ = 0, als de
aardbeweging en de invallende straling loodrecht op elkaar
staan. De aberratie bereikt dan zijn maximale
waarde. De uitdrukking reduceert dan tot cos φ' = – v/c over, wat
overeenkomt met de klassieke formule sinus θ = v/c .
Zie figuur 704 en bedenk dat voor de hoeken geldt: sin θ
= cos φ'.
Eenmaal per jaar beweegt de aarde met maximale
snelheid in de richting van de ster. Dan is de
hoek φ'
precies gelijk aan de hoogte boven de
ecliptica. De aberratie is dan kleiner dan
wanneer de aarde loodrecht op het invallende
licht beweegt. De aberratie vormt in de loop
van een jaar een horizontaal liggende ellips
rond de gemiddelde plaats van de ster met een
lange as van bijna 41'' .
 | Als we in de richting bewegen van de ster is -v/c
positief, want v en c zijn dan tegengesteld gericht. Het minteken
werkt hier een beetje verwarrend. |
De klassieke formule ging er van uit dat het licht van de ster loodrecht op
de beweging van de aarde stond, terwijl Einstein en Lorentz laten zien dat de
positie van de ster, vanaf de aarde gezien, daadwerkelijk is veranderd waardoor het licht enigszins
scheef invalt. Dan maakt het niet meer uit welke snelheid het
licht in de sterrenkijker heeft.
Intensiteit
Tenslotte vraagt Einstein zich af (blz. 912) of de amplitudo (= de
grootste waarde) van de golven verandert wanneer de golven worden waargenomen in
het stelsel-in-beweging. Dat is een "nieuwe" vraag, waar zijn
tijdgenoten niet mee zaten, behalve natuurlijk Lorentz (Versuch einer Theorie
blz. 108).
De oplossing wordt door Einstein in een paar regels gegeven: wanneer de
amplitudo van de elektromagnetische golven in het stelsel-in-rust wordt
aangegeven met A en de amplitudo in het stelsel-in-beweging met A'
, dan geldt de volgende betrekking
A' 2 = A2 . 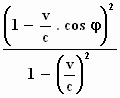 . .
Dat valt echt uit de lucht! Hoe komt hij er bij?
Wanneer je denkt dit even af te leiden uit de getransformeerde formules X’,
Y’ en Z’, dan kan dat lelijk tegenvallen als je de neiging hebt
af te dwalen langs aantrekkelijke gedachte–paadjes. Wekenlang heeft uw gids
ieder moment van zijn vrije tijd gebruikt om te achterhalen hoe Einstein tot
deze formule is gekomen. Hij lijkt natuurlijk verschrikkelijk veel op de formule
die de relatie tussen de hoekfrequenties weergeeft maar hoe komen we er aan.
Welke gedachtegang zit er achter. Het moet iets vanzelfsprekends zijn, maar je moet
het wel eerst even zien. Als je het zelf wil uitzoeken, klap dan snel dit manuscript
dicht en huur bijvoorbeeld een huisje in Drenthe (om meerdere redenen aanbevolen)
om er ongestoord enkele weken door te brengen.
Zo niet, dan volgt hier een uitweg uit het probleem.
De elektromagnetische golf is een transversale golf. De amplitudo staat dus
loodrecht op de richting waarin de golf zich voortbeweegt. We kijken uitsluitend
naar de elektrische vector (voor de magnetische vector geldt een gelijksoortig
verhaal). Wanneer de golf zich langs de x–as zou bewegen, zou de
elektrische vector alleen uit de y–component Y = Y0. sin Φ
en de z–component Z = Z0. sin Φ
bestaan. De grootste waarde van de y–component is Y0
en van de z–component Z0 (zie figuur 706).
Voor de amplitudo A geldt dan: A2 = Y02
+ Z02.
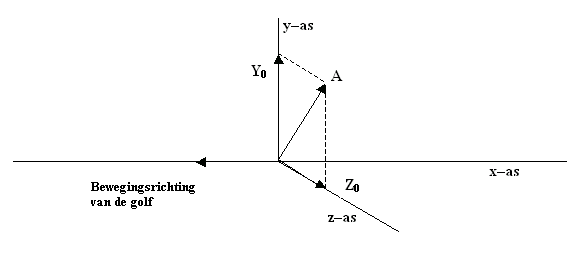
Figuur 706 Elektromagnetische golf langs de x–as
Wanneer de golf een hoek maakt met de x–as krijgt de elektrische
vector ook een x–component (zie figuur 707). De vectoren A,
Z0 en Ax y liggen in het vlak loodrecht op
de bewegingsrichting van de golf. In de tekening is een hulp–assenstelsel
getekend. De componenten van A in dit hulp–assenstelsel zijn X0,
Y0 en Z0. De vector Ayz is de
vectorsom van Y0 en Z0.
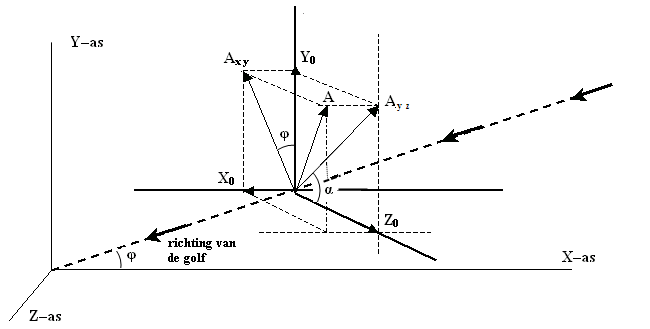
Figuur 707 Elektromagnetische golf die onder een hoek φ
t.o.v. de x–as voortbeweegt.
We moeten eerst het vlak in ogenschouw nemen dat gevormd wordt door de x–as
(tevens de bewegingsrichting van het stelsel–in–beweging) en de richting van
waaruit de straling tot ons komt. In het stelsel-in-beweging hebben we met
precies hetzelfde vlak te maken. We kunnen dus de richting van het licht in het
stelsel-in-rust en de richting van het licht in het stelsel-in-beweging in één
vlak tekenen (fig. 708). Dit vlak is het xy–vlak.
Wanneer dezelfde lichtgolf bekeken wordt vanuit een stelsel–in–beweging
dat langs de x-as beweegt, zal vanwege de aberratie de voortplantingsrichting van de golf en dus ook de
richting van de bron een andere waarde aannemen. De hoek wordt φ'
(zie figuur 708). Einstein beweert dat de amplitudo, en dat is een maat
voor de intensiteit van de straling, verandert als je overstapt van een stelsel–in–rust
naar een stelsel–in–beweging. Het zal zo uitpakken, dat zullen we straks
laten zien, dat op gelijke afstand de intensiteit groter is voor een stelsel–in–beweging
dat naar de bron toe beweegt dan voor een stelsel–in–rust (en omgekeerd).
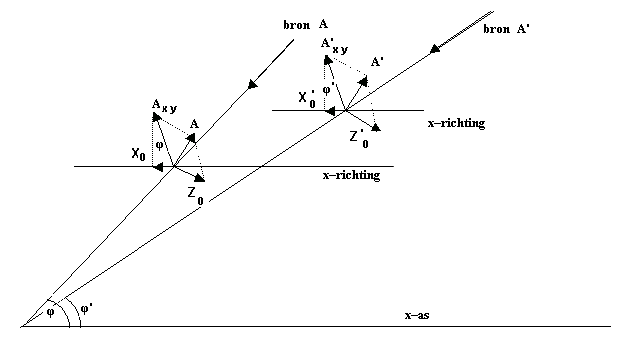
Figuur 708 De bron A gezien vanuit het stelsel–in–rust en dezelfde bron
A' gezien vanuit het stelsel–in–beweging .
We zoeken het nu uit.
Uit de transformatieformules blijkt dat de x–component X van
het elektrisch veld niet verandert bij de overgang van het stelsel-in-rust naar
het stelsel-in-beweging. Daarom richten we onze aandacht op X0,
de x–component van de amplitudo.
Met behulp van figuur 707 is te zien dat X0 = Axy
.
sin φ.
In het stelsel–in–beweging zal gelden X'0 = A'xy
. sin φ'.
Omdat X0 = X'0 volgt hieruit dat A'xy
= Axy. 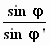
Maar als de component A'xy van A' met de factor 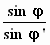 groter is dan Axy dan moet A' zelf ook met de factor
groter is dan Axy dan moet A' zelf ook met de factor 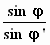 groter zijn dan A en ook de component Z'0 moet met die
factor zijn toegenomen.
groter zijn dan A en ook de component Z'0 moet met die
factor zijn toegenomen.
Terwijl bij de afmetingen van een object gold dat deze in de y– en z–richtingen
onveranderd bleven en dat er in de x–richting een verkorting optrad, geldt
voor de elektromagnetische golven dat de grootte in de x–richting
onveranderd blijft en dat er in de y– en z–richtingen een vergroting
optreedt.
We zijn er hierbij van uitgegaan dat de vector A'yz niet van richting is
veranderd t.o.v. Ayz,.
We mogen dus schrijven: A' = A . 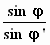
In het volgende maken we gebruik van sin2 φ'
= 1 – cos2 φ'
en de aberratieformule voor de verandering van de richtingscosinus
cos φ'
= 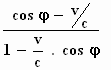
De gelijkheid blijft bestaan als je beide kanten in het kwadraat neemt.
Daarmee krijg je:
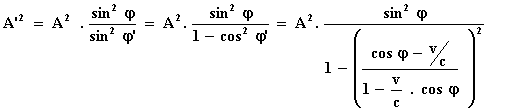
Teller en noemer vermenigvuldigen we met:
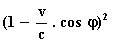
= A2 . 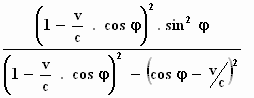
en de noemer
werken we uit:
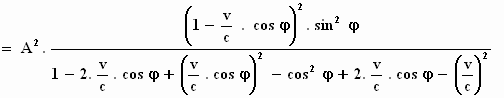
De termen 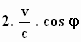 in de noemer vallen tegen
elkaar weg en we kunnen de noemer schrijven als: 1 – cos2φ
+ (v/c)2. (cos2φ
–1). in de noemer vallen tegen
elkaar weg en we kunnen de noemer schrijven als: 1 – cos2φ
+ (v/c)2. (cos2φ
–1).
Dit kan worden vereenvoudigd tot sin2φ
– (v/c)2. sin2φ
= 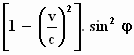 . .
Wanneer we dit invullen voor de noemer, dan zien we dat de sin2φ
in de teller en de noemer tegen elkaar kunnen worden weggestreept. We houden
precies de uitdrukking over waar we naar opzoek waren:
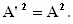 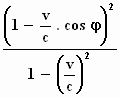
Dat valt niet mee. Dat moet ook voor zijn tijdgenoten even puzzelen zijn
geweest. Wat Einstein vervolgens hieruit concludeert, is toch heel verstrekkend.
Stel dat φ gelijk is aan nul,
dus cos φ = 1.
Je beweegt recht
op de bron af, waarbij v/c negatief is.
Bedenk dat 1 – (v/c)2 = (1 – v/c) . (1 + v/c) , dan
houd je over:
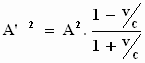
Als v de lichtsnelheid benadert, nadert v/c de waarde –1.
De noemer gaat naar nul, waardoor de uitdrukking naar oneindig gaat. Zoals
Einstein zegt: "De lichtbron wordt oneindig intensief".
Lorentz kwam niet verder dan een verdubbeling van de energie.
Dat was schrikken.
Nog even dit: we gingen er bij deze uitleg van uit dat de richting van de vector A
onveranderd blijft bij de overgang van het ene stelsel naar het andere. Die hoek
blijft behouden. Dat heeft de volgende natuurkundige achtergrond:
We gaan uit van gepolariseerd licht. Stel dat je een polarisatiefilter (een
polaroid) verticaal in het yz-vlak hebt opgesteld . Dan kan je het licht uitdoven door het
polaroid om zijn x-as te draaien tot een hoek waarbij het polaroid loodrecht op de
lichtvector A staat. Omdat in het bewegende stelsel de afmetingen in de y–
en z–richting niet veranderen, behoudt het polaroid in het stelsel–in–beweging
deze hoek. Als de lichtvector echter zou zijn gedraaid, zou het licht in het
bewegende stelsel minder worden uitgedoofd. De bewegende waarnemer constateert
licht waar de stilstaande waarnemer geen licht constateert. Dat nu is zelfs voor
de relativiteitstheorie te gortig: dat is fysisch onmogelijk.
Dit betekent (zie figuur 707): tg α =
constant of Y0/Z0 = Y'0/Z'0.
Dit gaan we ook bewijzen, maar je mag ook wel iets anders gaan doen als je het wel
gelooft.
We zullen eerst aantonen dat Y'/Z' = Y/Z. De hoek (zie figuur 709)
die de elektrische vector maakt, kan je vinden uit tg α
= Y0/Z0 en de hoek die de magnetische vector
maakt, is te vinden uit tg δ = M0/N0
. De elektrische en de magnetische vector staan loodrecht op elkaar.
In deze figuur is α = 90º +
δ . Hieruit volgt tg α
= – tg δ , dus Y0/Z0 = – M0/N0.
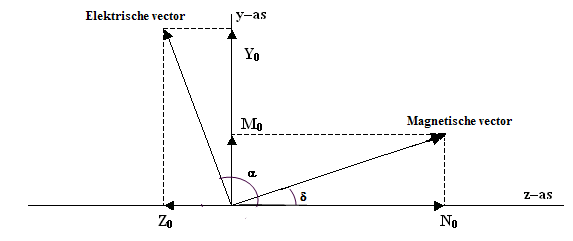
Figuur 709 De elektrische en de magnetische vector staan loodrecht op elkaar
Nu tonen we aan dat de richting van de elektrische vector in het
stelsel-in-beweging dezelfde is als in het stelsel-in-rust. De vraag: "Is Y'/Z' gelijk
aan Y/Z". We maken gebruik van de transformatie formules en de zojuist
geïntroduceerde relatie Y0/Z0 = – M0/N0
:
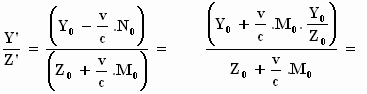
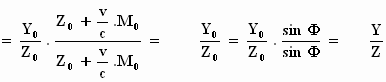
De richting van de amplitudo in het yz–vlak blijft dus behouden. De
formule voor de amplitudo in het stelsel–in–beweging klopt.
Hoe graag we Einstein ook op een gedachtefout willen betrappen, §7 moet onze
goedkeuring krijgen.
Terug
|
|