|
De uitdrukking voor de energiedichtheid A2/8π
, waarin A de amplitudo is, was een bekende formule die uit de
theorie van Maxwell 1) volgt.
J.C.Maxwell:" A treatise on electricity
and magnetism"’ deel 2 p. 440–441.
Zoals we in het begin van §4 hebben gezien, geldt voor de punten (x,
y, z) op een boloppervlak met de straal R:
x2 + y2 + z2 = R2.
Bekijk vanuit het stelsel–in–rust een "hoeveelheid licht" dat
zich in een bolvormig volume bevindt.
Denk aan vlakke golven die zich door de ruimte spoeden. Het bolvormige volume
beweegt mee met het licht. De hoeveelheid licht die in de bol zit, blijft dus
hetzelfde.
We volgen een lichtstraal in een willekeurige richting, waarvoor de
richtingscosinussen a, b en d gelden (zie fig. 801). De
formule voor de straal R van deze bol op het tijdstip t is:
(x – a.c.t)2 + (y – b.c.t)2 + (z – d.c.t)2
= R2 (Voortijlende bol)
Het centrum van de bol bevindt zich op het tijdstip t op de plaats (act,
bct, dct). Ga zelf na dat (act, bct, dct) een rechte lijn door de
oorsprong voorstelt als je t allerlei verschillende waarden geeft. Met
positieve waarden voor a, b, en d krijg je een beweging zoals in figuur
801 is weergegeven.
 | Iemand vraagt zich misschien af hoe een bol een snelheid gelijk aan die
van het licht kan hebben, terwijl we eerder hebben gezien dat een bol met
die snelheid zo plat als een pannenkoek is. Daar heb je een punt! |
 | Als wij in het stelsel–in–rust deze vorm als een bol zien, moet de
vorm in het stelsel–in–beweging, dat met de lichtsnelheid voortbeweegt,
oneindig groot zijn in de bewegingsrichting. De afmetingen zijn immers γ
keer zo groot in het stelsel–in–beweging, omdat wij in het stelsel–in–rust
de afmetingen γ keer zo klein zien. Denk aan de balk met de cowboys erop,
die werd door ons als korter gemeten. Zoals je weet: 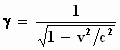 .
Met v=c wordt γ gelijk aan
oneindig. Als je zelf met de voorkant van de bol zou meebewegen, zou je de
achterkant van de bol nooit kunnen waarnemen, want het licht van de achterkant
kan nooit de voorkant bereiken. Voor– en achterkant
zijn dan "oneindig ver" van elkaar verwijderd. .
Met v=c wordt γ gelijk aan
oneindig. Als je zelf met de voorkant van de bol zou meebewegen, zou je de
achterkant van de bol nooit kunnen waarnemen, want het licht van de achterkant
kan nooit de voorkant bereiken. Voor– en achterkant
zijn dan "oneindig ver" van elkaar verwijderd.
Wij kunnen ons dus een bolvormig volume voorstellen dat zich met de
lichtsnelheid voortbeweegt. |
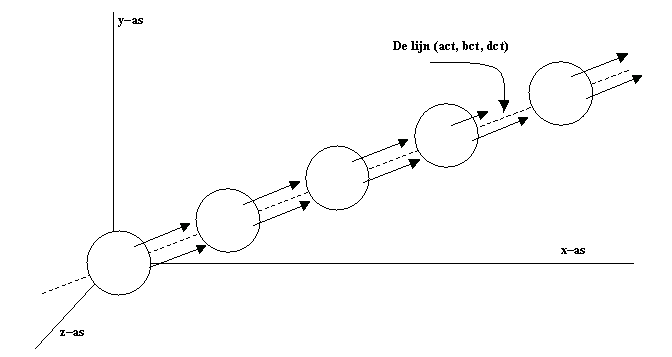
Figuur 801 Het met de lichtsnelheid voortvliegende bolvormige volume
Het bolvormige volume zoals we dat in het stelsel–in–rust waarnemen, zal
niet meer bolvormig zijn als het wordt waargenomen vanuit een stelsel–in–beweging.
Daartoe zullen we de coördinaten van de bol gewoon transformeren.
Je herinnert je de transformatieformules:
x = γ (x – v.t)
h = y
ζ = z τ = γ (t – 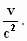 x) x)
waarmee de coördinaten in het stelsel-in-rust kunnen worden omgerekend naar
de coördinaten in het stelsel-in-beweging en omgekeerd. We hebben zoiets eerder
gezien. In §4 gingen we uit van een bol in het bewegende stelsel,
waarvoor geldt x2 + h2 + ζ2 = R2.
Daar konden we probleemloos de transformatieformules invullen om de ellipsoïde
te vinden die we in het stelsel-in-rust zouden waarnemen. Maar nu hebben we een
bol in het stelsel-in-rust, we moeten nu terugtransformeren, om de vorm
te vinden in het stelsel-in-beweging. Dat gaat simpeler dan je tevoren zou
denken. Beide stelsels zijn namelijk gelijkwaardig. Je mag het
stelsel-in-beweging rustig opvatten als het stelsel-in-rust en het
stelsel-in-rust zien als het stelsel-in-beweging dat met een snelheid –v
ten opzichte van jouw stelsel beweegt. Dan verwissel je x voor ξ,
enzovoort, en v voor –v en je krijgt de volgende
transformatieformules voor x, y, z en t:
x = γ ( x
+ v.τ); y =
h
; z = ζ ;
t = γ(τ
+ 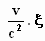 ) )
met
γ = 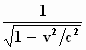
Omdat verder de vorm van de voortijlende "bol" niet afhangt van het
tijdstip waarop je er naar kijkt, nemen we voor dat tijdstip, heel slim, τ
= 0. Het centrum van de bol bevindt zich dan in de oorsprong van
beide stelsels. Bedenk dat voor t = τ = 0
de oorsprong van het stelsel–in–beweging net de oorsprong van het stelsel–in–rust
passeert.
Je kan eerst de formule voor de "Voortijlende bol" compleet
uitschrijven en daarna τ =
0 invullen, maar dat blijkt geen verschil te maken het direct vereenvoudigen
van de transformatieformules met τ = 0.
Dan worden x en t eenvoudig: x = γ
. x en t =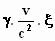 . Aan y en z verandert niets. De getransformeerde bol, de "Voortijlende
bol" bol gezien vanuit het stelsel-in-beweging op het tijdstip τ
= 0 wordt dan:
. Aan y en z verandert niets. De getransformeerde bol, de "Voortijlende
bol" bol gezien vanuit het stelsel-in-beweging op het tijdstip τ
= 0 wordt dan:
(γ.x
– a. c. 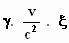 )2
+ (h
– b.c. )2
+ (h
– b.c. 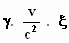 )2
+ (ζ – d.c. )2
+ (ζ – d.c. 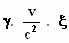 )2
= R2 . )2
= R2 .
Dit kunnen we nog een beetje vereenvoudigen tot:
γ 2. (x – a. 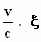 )2
+ (h
– b. γ
. )2
+ (h
– b. γ
. 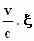 )2
+ (ζ – d. γ. )2
+ (ζ – d. γ. 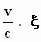 )2
= R2 .
Wanneer je nu denkt; "Dit wordt mij allemaal teveel!", kijk dan
eens naar de Alternatieve afleiding bij §8. )2
= R2 .
Wanneer je nu denkt; "Dit wordt mij allemaal teveel!", kijk dan
eens naar de Alternatieve afleiding bij §8.
Om te begrijpen wat dit voor een vorm is, bekijken we eerst eens het
resultaat voor ξ = 0:
h2 + ζ2
= R2
Dit is een cirkel met straal R. De betekenis hiervan is dat in het
stelsel-in-beweging de bol in het ηζ–vlak
loodrecht op de voortplantingsrichting van dit stelsel, nog steeds een grootste
cirkel met straal R als doorsnede heeft. De bol is echter afgeplat of
opgerekt in de x–richting en vervormd met
een as in de bewegingsrichting van de bol. Een soort ellipsoïde (zie fig.
802).
We proberen de lengte van de bol in de x–richting
te vinden.
Bij zekere x wordt de omtrek van de
"bol" in het verticale vlak gegeven door de cirkel:
(h – b. γ
. 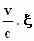 )2
+ (ζ – d. γ. )2
+ (ζ – d. γ. 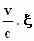 )2
= R2 – γ2.
(x – a. )2
= R2 – γ2.
(x – a. 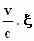 )2 )2
met het middelpunt (h *, ζ*)
= (b. γ . 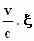 , d. γ.
, d. γ. 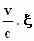 ). ).
De middelpunten vormen een lijn vanuit het centrum in de richting van de
bewegingsrichting van de "bol" tot aan de rand van de "bol".
De straal van de verticale cirkel op de plaats x wordt
gevonden via de wortel uit
R2 – γ2.
(x – a. 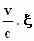 )2. )2.
Deze straal wordt nul als R2 – γ2.
(x – a. 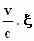 )2
= 0 )2
= 0
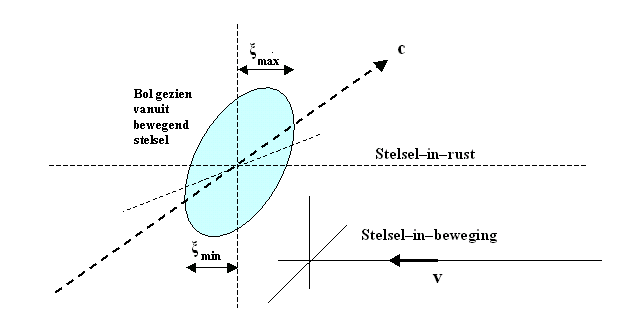
Figuur 802 De scheef getrokken, afgeplatte bol als het stelsel–in–beweging
de bol tegemoet komt
Hieruit volgt:
x = + of – 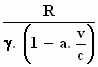
Van deze merkwaardige vorm kunnen we de inhoud berekenen door de oppervlakten
van de verticale cirkels te integreren vanaf het punt
x min = 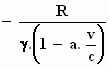
tot aan het punt
x
max = 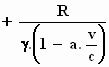
De inhoud S' wordt dan gevonden door van het punt x
min tot aan het punt x max
te integreren:
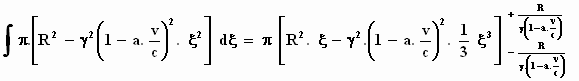
Invullen en zorgvuldig uitwerken levert: S' =
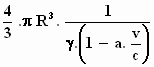
De inhoud van de bol in het stelsel–in–rust is: S = 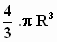
De verhouding is dus: 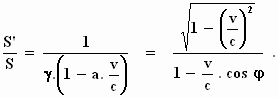
Achter het laatste (=) teken is voor de richtingscosinus a de waarde cos
φ ingevuld en voor γ
is ingevuld
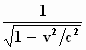 . .
 | Let op: als het stelsel–in–beweging de bol tegemoet komt is v/c
negatief en dan is S'/S < 1 . De bol is in de x–richting afgeplat.
Omgekeerd als het stelsel–in–beweging tracht te ontkomen aan de bol, dan
is v/c positief en S'/S > 1. De bol is in de x–richting uitgerekt. |
De inhoud van de vervormde bol kan ook zonder integreren worden gevonden.
Omdat de bol gewoon uit cirkelvormige plakken bestaat, die in het verticale
vlak een beetje verschoven zijn ten opzichte van elkaar, mag je ze in
gedachten weer goed schuiven en dan hou je een ellipsoïde over, een
omwentelingslichaam rond de x–as, met een straal in horizontale richting
van 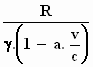 .
Bij een bol is die straal R, dus heeft deze ellipsoïde een inhoud die .
Bij een bol is die straal R, dus heeft deze ellipsoïde een inhoud die 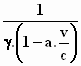 keer
zo groot is, precies de waarde die we hierboven hadden afgeleid. Misschien
dat Einstein deze methode bedoelde in zijn artikel waar hij zegt: "…..laat
een eenvoudige berekening zien dat …..". keer
zo groot is, precies de waarde die we hierboven hadden afgeleid. Misschien
dat Einstein deze methode bedoelde in zijn artikel waar hij zegt: "…..laat
een eenvoudige berekening zien dat …..".
Je zou het bijna vergeten, maar we waren bezig te achterhalen hoeveel
lichtenergie E in het stelsel-in-rust in de bol wordt waargenomen en
hoeveel vanuit het bewegende stelsel wordt waargenomen. Daartoe moet de gevonden
verhouding worden vermenigvuldigd met de lichtenergie per volume-eenheid A' 2/8π
respectievelijk A2 / 8π.
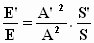
We maken nu gebruik van de net gevonden verhouding S' / S en wanneer
je tegelijkertijd gebruik maakt van de uitdrukking voor de amplitudo in het
stelsel–in–beweging van de vorige paragraaf:
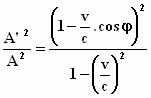
levert het als uitkomst op:
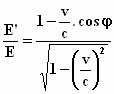
Om de betekenis hiervan te begrijpen, stelt Einstein voor om de formule te
bekijken voor de situatie dat het bewegende stelsel en de bewegingsrichting van
de bol samenvallen: φ = 0 , dus cos
φ = 1. We krijgen dan op eenzelfde
manier als in de vorige paragraaf voor de verhouding A'2/A2
van de intensiteit:
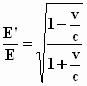
 |
Dit stukje besluit Einstein met op te merken dat
het toch wel merkwaardig is dat de energie-inhoud van de
lichthoeveelheid op dezelfde manier verandert als de frequentie (zie
§7 Dopplereffect). Dat lijkt een verkapte manier om te vertellen dat
de theorie die hij enige maanden tevoren had gelanceerd over het
foto-elektrisch effect, waarbij hij aannam dat licht uit
"lichtdeeltjes" bestaat met een energie die evenredig is met
de frequentie, een stevige steun in de rug krijgt met het net
afgeleide resultaat. |
Terug
In het vervolg van deze paragraaf gaat Einstein in op een probleem dat in de
literatuur toentertijd heftig 1) werd besproken: de stralingsdruk,
speciaal op een spiegelend vlak. Maxwell was er al over begonnen en opperde dat
het misschien mogelijk zou zijn mechanische energie te winnen door licht op een
vlak te laten vallen (in een vacuüm) dat daardoor in beweging zou worden
gebracht. Einstein moet goed op de hoogte zijn geweest van de discussies.
1 ) Zie bijvoorbeeld Max Abraham: "Zur Theorie der Strahlung und
des Strahlunsdruckes", Annalen der Physic IV, band 14, p. 236, 1904
Hij gaat uit (blz. 914) van een volmaakte spiegel (100 % reflectie)
die in het vlak x = 0 verticaal staat
opgesteld. De spiegel is dus opgesteld in de oorsprong van het
stelsel-in-beweging. We maken gebruik van vlakke golven, zodat de formules die
in de vorige paragraaf en in het eerste deel van de huidige paragraaf werden
afgeleid, van toepassing zijn. De vraag is welke lichtdruk op de spiegel wordt
uitgeoefend en welke frequentie, welke intensiteit en welke richting het
gereflecteerde licht zal hebben.
Als, bezien vanuit het stelsel-in-rust, voor de invallende bundel de
amplitudo A , de richtingscosinus cos φ
en de frequentie f is, dan gelden, zoals we hebben afgeleid, in het
stelsel-in-beweging voor A', cos φ'
en f ' de volgende uitdrukkingen,
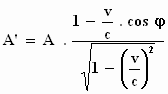 ;
(amplitudo) ;
(amplitudo)
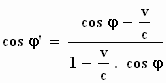 ;
(richtingscosinus) ;
(richtingscosinus)
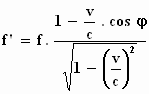 (frequentie)
(frequentie)
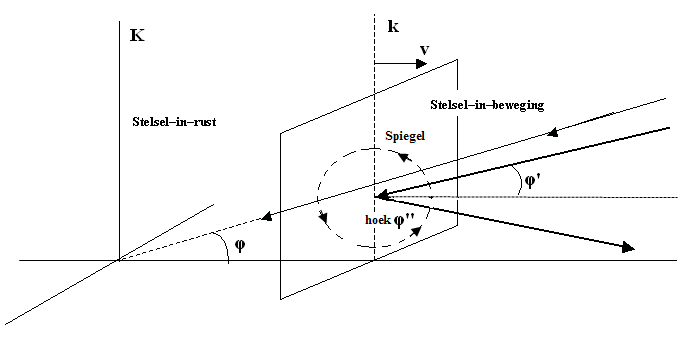
Figuur 803 Reflectie tegen een bewegende, volmaakte spiegel
Wanneer we met de spiegel zouden meebewegen en we zouden de amplitudo, de
richtingscosinus en de frequentie aangeven met A'' , cos φ''
en f'' , dan zou het volgende gelden:
A'' = A' ;
cos φ'' = – cos φ' ;
f '' = f '
Immers, we hebben dan te maken met een voor ons stilstaande spiegel, waarvoor
de normale reflectie-eigenschappen gelden: de amplitudo. noch de frequentie
veranderen. Alleen de hoek verandert.
De hoek φ'' van de
teruggekaatste bundel wordt 180° – φ',
vandaar het minteken.
Om er achter te komen welke amplitudo A''', welke frequentie f'''
en welke richtingscosinus φ'''
het licht dan in het stelsel-in-rust K zal hebben, dienen we even
"gezellig" terug te transformeren, van het stelsel–in–beweging
naar het stelsel–in–rust . Let op: bij dit terugtransformeren moeten we voor
de snelheid – v invullen. Je krijgt:
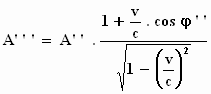
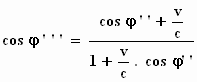
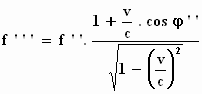
Voor de grootheden met de dubbele accenten vullen we vervolgens de
uitdrukkingen in die enkele regels terug staan aangegeven met een pijltje.
Daarmee verkrijgen we:
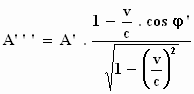
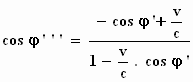
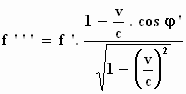
Vervolgens kunnen we in deze laatst gevonden uitdrukkingen de grootheden met
één accent vervangen door de uitdrukkingen van nog iets verder terug. We
werken de zaak direct uit. Laat je niet afschrikken, het is niet veel meer dan
breuken vereenvoudigen en wat haakjes wegwerken, maar het moet zorgvuldig
gebeuren.
Voor de amplitudo A ''' krijgen we:
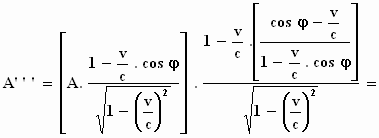 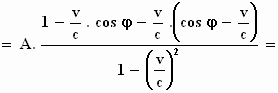
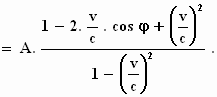
De richtingscosinus cos φ'''
wordt:
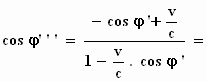
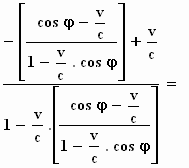
Vermenigvuldig de hele teller en de hele noemer met (1 – 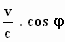 )
: )
:
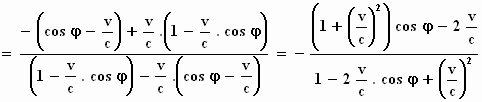
Tenslotte verkrijgen we voor de frequentie f ''' :
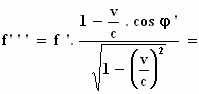
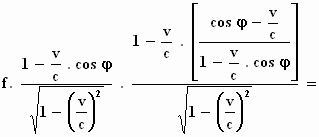
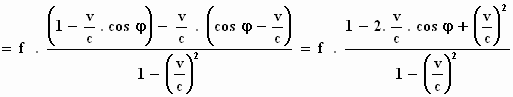
Mooi, maar wat willen we hier eigenlijk mee?
Het zijn behoorlijk ingewikkelde uitdrukkingen, die de eigenschappen van de
teruggekaatste bundel karakteriseren. Einstein laat één voorbeeld zien van wat
je er mee kan doen. Hij leidt een formule af voor de druk p die het licht
op de bewegende spiegel uitoefent bij het weerkaatsen. We zoeken dat uit.
Bedenk dat de druk de kracht per oppervlakte–eenheid is. Als de kracht op
een oppervlak werkt dat zich verplaatst, dan is de arbeid die verricht wordt:
kracht maal verplaatsing. Deze arbeid is de energie van de bundel die voor de
bundel verloren gaat.
Het maakt bij dit laatste niet uit wat de oorzaak is van het verplaatsen
van de spiegel, de spiegel verplaatst zich niet vanwege het licht dat er op
valt, maar toch verricht de opvallende bundel arbeid. Je kan zeggen dat de
bundel het verplaatsen wat moeilijker of gemakkelijker maakt, afhankelijk van
de bewegingsrichting van de spiegel.
Hoeveel energie bevat de opvallende bundel (zie fig. 804) en de
teruggekaatste bundel, gezien vanuit het stelsel–in–rust, dat is de kwestie.
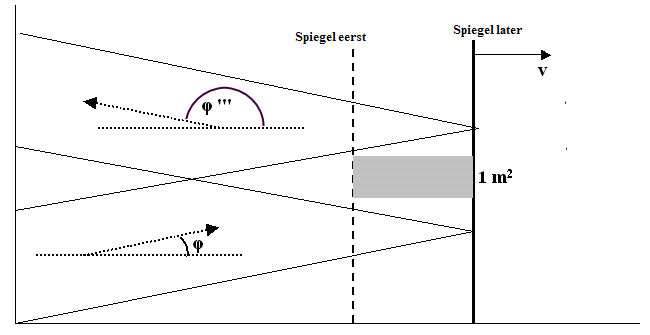
Figuur 804 Opvallende en teruggekaatste bundel tegen een bewegende
spiegel
De energie per volume–eenheid van de opvallende bundel wordt door de
uitdrukking A2/ 8π
gegeven. Een lichtbundel met een dwarsdoorsnede van 1 m2 en een
lengte van c meter bevat een hoeveelheid energie gelijk aan c. A2
/ 8π joule. Dat is de
hoeveelheid energie die in 1 seconde loodrecht op een oppervlakte van 1
m2 valt.
De lichtbundel komt echter onder een hoek φ
op de spiegel. De energie wordt in toenemende mate verspreid over het oppervlak
van de spiegel als de hoek φ
groter wordt en de betreffende m2
ontvangt dus minder licht.
Laten we eerst even uitgaan van een stilstaande spiegel. De bundel die daar
in één seconde tegenaan komt, heeft een lengte van c meter. Wanneer de
bundel onder een hoek φ
op een oppervlakte van 1 m2 tegen de spiegel
kaatst, moet de dwarsdoorsnede
van die bundel cos φ m2
zijn. De energie in de lichtbundel ter lengte c meter is dus:
c. cos φ. A2 / 8π
(Simpel hè)
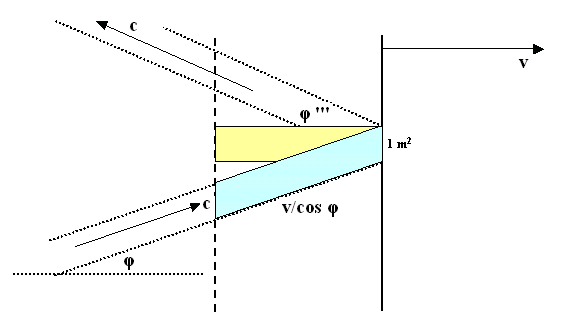
Figuur 805 Energie die de spiegel bereikt
De spiegel beweegt echter. Een deel van de lichtenergie heeft in 1 seconde
nog niet de spiegel bereikt. In figuur 805 is het stukje bundel dat de
spiegel nog niet heeft bereikt met de kleur lichtblauw weergegeven. Het heeft
een lengte van v / cos φ meter
en een dwarsdoorsnede van cos φ m2.
De inhoud van dit stukje bundel is v m3, even groot als
van het gele stukje bundel dat er half achter verscholen ligt. Het bevat een
hoeveelheid energie:
v . A2 / 8π
(joule)
De hoeveelheid lichtenergie waar de spiegel in 1 seconde door wordt
getroffen, is dus:
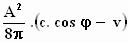
De hoeveelheid lichtenergie die in 1 seconde wordt gereflecteerd, is:
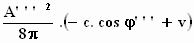
Het verschil tussen deze twee uitdrukkingen is de arbeid die door de
lichtbundel op de spiegel is verricht:
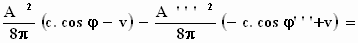
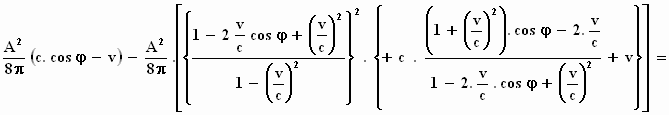
"Is dit nog leuk? Dit loopt echt de spuigaten uit. Valt hier nog iets
aardigs van te maken?"
Het gebruikelijke recept is: netjes uitwerken en niet mopperen! Na een aantal
keren, omdat je onderweg - naar goed gebruik - wat fouten maakt, zal je zeker goed uitkomen.
Het is overigens een te gekke oefening voor de aankomende student om voor
eens en voor altijd goed met haakjes te leren werken.
Mocht je er zelf niet uitkomen, dan moet je je verlaten op het geloof in de
uitkomst:
Het energieverschil = 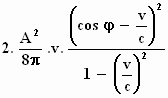
Het positieve energieverschil wordt veroorzaakt door de arbeid die de
lichtbundel op de spiegel heeft uitgeoefend. De spiegel beweegt ook in de
richting waarin de bundel hem zou doen verplaatsen als de bundel de enige kracht
was die op de spiegel werkte.
Omdat arbeid gelijk is aan kracht x weg en de weg in 1 seconde gelijk
is aan de afstand v , kunnen we uit de gevonden uitdrukking de kracht
halen door de uitdrukking door v te delen. Aangezien we de bundel op 1
m2 lieten vallen, levert dit de kracht per oppervlakte-eenheid,
dat wil zeggen: de druk p.
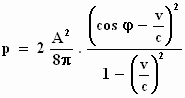
Deze formule vinden we in het eerder aangehaalde artikel van M.Abraham op
blz. 257 terug. De afleiding tot dit resultaat is echter aanmerkelijk
ondoorzichtiger dan die van Einstein.
Bij dit resultaat zegt Einstein bescheiden dat als je v/c verwaarloost
je de formule krijgt die uit laboratoriummetingen en andere theorieën al bekend was,
namelijk:
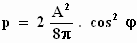
om te eindigen met de opmerking dat je alle problemen uit de optica, die te
maken hebben met het in beweging zijn van de bron of de waarnemer of een
tussenliggend medium, op kan lossen door het probleem terug te brengen tot een
probleem in het stelsel-in-rust.
(Hartstikke makkelijk! Gewoon doen!)
Terug
|