§ 9. De transformatie van de Maxwell–Hertz vergelijkingen met inbegrip
van elektrische stromen.
We gaan uit van de vergelijkingen:
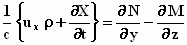 ;
; 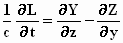
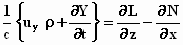 ;
;
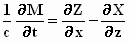
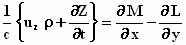 ;
;
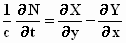
waarbij
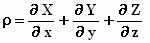
en de betekenis heeft van de 4 π-voudige elektrische
ladingsdichtheid, waarbij (ux , uy
,
uz ) de snelheidsvector van deze elektriciteit weergeeft.
Als men zich de elektrische lading voorstelt als onveranderlijk gebonden aan
kleine, starre deeltjes (ionen, elektronen), dan vormen deze vergelijkingen de
elektromagnetische basis van de door Lorentz opgestelde theorie van de
elektrodynamica en optica van bewegende voorwerpen.
Vervolgens transformeren wij deze vergelijkingen, die in het stelsel K
gelden, met behulp van de transformatieformules van § 3 en § 6 naar het
stelsel k en we verkrijgen de vergelijkingen:
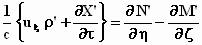 ;
; 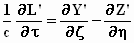 ,
,
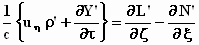 ;
;
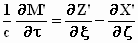 ,
,
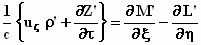 ;
; 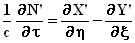 ,
,
waarbij
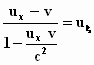
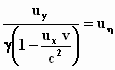 en
en
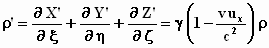 .
.
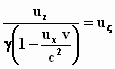
Aangezien de vector (uξ, uη,
uζ ) niets anders is dan de snelheid van het
elektrische deeltje gemeten in het stelsel k – zoals uit de
optelformule voor snelheden (§ 5) volgt – is daarmee aangetoond dat op grond
van onze kinematische principes de elektrodynamische basis van de theorie van
Lorentz over de elektrodynamica van een bewegend voorwerp in overeenstemming is
met het relativiteitsprincipe.
Ik wil hier nog een korte opmerking aan toevoegen, namelijk dat uit de
afgeleide vergelijkingen eenvoudig de volgende belangrijke stelling kan worden
opgemaakt: Als een elektrisch geladen voorwerp willekeurig in de ruimte beweegt
waarbij zijn lading, gezien vanuit een coördinatenstelsel dat met het voorwerp
meebeweegt, niet verandert, dan blijft zijn lading ook gezien vanuit het
"rustende" stelsel K constant.
Terug
