§8   De transformatie van de energie van de lichtstralen. Theorie over de stralingsdruk die op een perfecte spiegel wordt uitgeoefend.

Omdat A² / 8 π gelijk is aan de lichtenergie per volume-eenheid moeten we volgens het relativiteitsprincipe A’² / 8 π als de lichtenergie in het stelsel-in-beweging opvatten. De verhouding A ’²/ A² zou de verhouding tussen de "bewegend gemeten"en "in rust gemeten" energie van een hoeveelheid  licht moeten zijn, mits het volume in K of in k gemeten hetzelfde is. Dit is echter niet het geval. Als a, b, d de richtingscosinussen van de normaal op de lichtgolf zijn in het stelsel-in-rust, dan passeert er door de oppervlakte van een met de lichtsnelheid bewegend boloppervlak

(x – c.a.t)² + (y – c.b.t)² + (z – c.d.t)² = R²

geen energie; we kunnen daarom zeggen dat dit vlak voortdurend dezelfde hoeveelheid licht insluit. We vragen ons af welke energiehoeveelheid door dit vlak, beschouwd in het stelsel k, wordt omsloten, dat wil zeggen de energiehoeveelheid van die hoeveelheid licht ten opzichte van het stelsel k.
Het boloppervlak vormt – beschouwd in het stelsel-in-beweging – een ellipsoïde, waarvoor op het tijdstip τ = 0 de vergelijking geldt

( γ ξ – a .γ .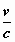 . ξ )² + ( η – b . γ . 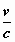. ξ )² + ( ζ – d . γ . 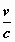. ξ )² = R²

Als we het volume van de bol S noemen en van de ellipsoïde S’ laat een eenvoudige berekening zien dat:

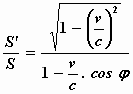
Als we dus de in het stelsel-in-rust gemeten lichtenergie E noemen en E’ de in het stelsel-in-beweging gemeten lichtenergie, die zich binnen de ruimten bevinden die door de genoemde vlakken worden omsloten, dan verkrijgt men:

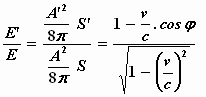
welke formule voor φ = 0 de volgende vereenvoudigde vorm aanneemt:

.

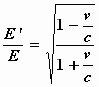Men dient er nota van te nemen dat de energie van een hoeveelheid licht volgens dezelfde wetmatigheid afhankelijk is van de bewegingstoestand van de waarnemer als de frequentie.

Laten we nu aannemen dat het vlak dat gevormd wordt door de coördinaat ξ = 0 een volkomen spiegelend vlak is, waartegen de in de laatste paragraaf beschouwde vlakke golven worden weerkaatst. We willen weten welke lichtdruk op het spiegelend vlak wordt uitgeoefend en welke richting, frequentie en intensiteit het licht zal hebben na de weerkaatsing.

Het invallende licht wordt (ten opzichte van het stelsel K) door de grootheden A, cos φ en f   gedefinieerd. Gezien vanuit k zijn de overeenkomstige grootheden:

Voor het weerkaatste licht verkrijgen we, als we het gebeuren vanuit het stelsel k beschouwen:

A’’ = A’ ,

cos φ’’ = – cos φ’ ,

f ’’ = f ‘ .

Zo verkrijgt men door terugtransformatie naar het stelsel-in-rust K voor het weerkaatste licht:

De energie die de spiegel per oppervlakte-eenheid en per tijdseenheid treft 
(gemeten in het stelsel-in-rust) is van zelfsprekend 
                            
De energie die zich per oppervlakte-eenheid en per tijdseenheid van de spiegel verwijdert, is 

Het verschil tussen deze beide uitdrukkingen is volgens de wet van behoud van energie de door de lichtdruk per tijdseenheid verrichte arbeid. Stelt men dit laatste gelijk aan het product p . v , waarbij p de lichtdruk  ¹) is, dan verkrijgt men:

De eerste benadering hiervan leidt tot de volgende uitdrukking, die in overeenstemming is met experimenten in het laboratorium en met andere theorieën

Met de hier gebruikte methode kunnen alle problemen uit de optica van voorwerpen die in beweging zijn, worden opgelost. Het belangrijkste is dat de elektrische en magnetische kracht van het licht dat door een bewegend voorwerp wordt beïnvloed naar een coördinatenstelsel wordt getransformeerd dat ten opzichte van het voorwerp in rust is. Zo kan elk probleem van de optica van  voorwerpen die in beweging zijn, worden teruggebracht tot de reeks van problemen uit de optica van voorwerpen–in–rust.

¹)Noot vertaler: Einstein gebruikt voor de lichtdruk het symbool P ,  maar we hebben in de vertaling voor de kleine letter p gekozen, in overeenstemming met het huidige gebruik van dit symbool  en ook om verwarring met het gangbare symbool voor vermogen P te voorkomen.

Terug