§ 4. De natuurkundige betekenis van de
verkregen vergelijkingen voor onvervormbare voorwerpen en klokken die in beweging zijn.
Laten wij een onvervormbare bol met een straal R
beschouwen, die ten opzichte van het stelsel-in-beweging k in rust
is, en waarvan het middelpunt zich in de oorsprong van dit coördinatenstelsel
bevindt. De vergelijking van het oppervlak, van deze ten opzichte van het
stelsel K met de snelheid v bewegende bol, is:
ξ2 + η2 + ζ2
= R2
De vergelijking van deze oppervlakte is, uitgedrukt in x
, y , z op het tijdstip t = 0 :
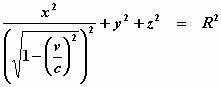
Een onvervormbaar voorwerp, dat, opgemeten in een toestand
van rust, de vorm heeft van een bol, heeft dus in een toestand van beweging –
beschouwd vanuit het stelsel-in-rust – de vorm van een omwentelingsellipsoïde
met de assen
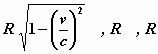
Terwijl dus de Y- en Z -
afmetingen van de bol (en dus ook van ieder ander onvervormbaar voorwerp van een
willekeurige vorm) zich ondanks de beweging ongewijzigd aan ons voordoen, laat
de X–afmeting een verkorting zien in de verhouding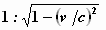 
. Een verkorting die toeneemt naarmate v groter is. Voor v = c schrompelen
alle bewegende voorwerpen – gezien vanuit het stelsel-in-rust – ineen tot
objecten die er plat uitzien. Voor snelheden groter dan de lichtsnelheid
verliezen onze overdenkingen hun zin, maar we zullen in de nog komende overwegingen
overigens tot de conclusie komen dat de lichtsnelheid in onze theorie, natuurkundig
gezien, de rol speelt van een oneindig grote snelheid.
─ Vanzelfsprekend gelden de eerder genoemde resultaten
ook voor voorwerpen die in rust zijn in het "stelsel-in-rust" en
vanuit een
eenparig bewegend stelsel worden beschouwd. ─
We stellen ons verder voor dat één van de klokken,
die als
hij in rust is ten opzichte van het stelsel-in-rust de tijd t
aangeeft en als hij in rust
is ten opzichte van het stelsel-in-beweging de tijd τ
aangeeft, zich in de oorsprong van het coördinatenstelsel k bevindt
en zo is afgesteld dat hij de tijd τ aangeeft. Hoe snel loopt
deze klok gezien vanuit het stelsel-in-rust?
Tussen de grootheden x , t en τ
gelden op de plaats van deze klok, zoals we weten, de vergelijkingen:
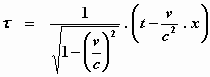
en
x = v . t
Er geldt dus
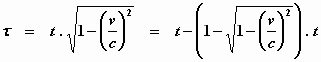
waaruit volgt dat per seconde de aanwijzing van de klok
(gezien vanuit het stelsel-in-rust) 
seconde achterloopt of ─ in een benadering waarbij de termen van de
vierde en hogere orde worden verwaarloosd ─ dat de klok
per seconde 
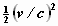seconde
achterloopt.
Dit leidt tot de volgende eigenaardige consequentie: als
in het stelsel-in-rust K in de punten A en B
gelijklopende klokken staan opgesteld en als men vervolgens de klok in A met een snelheid v
langs de verbindingslijn naar B verplaatst, dan lopen na aankomst
van deze klok in B de twee klokken niet meer gelijk, doch de klok
die van A naar B is verplaatst, loopt in
vergelijking tot de klok die vanaf het begin in B is gebleve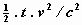n 
seconde achter (met een nauwkeurigheid van de eerder genoemde benadering),
waarbij t de tijd is die de klok er in het stelsel-in-rust K
over deed om van A naar B te gaan.
Men begrijpt direct dat dit resultaat nog steeds geldig is
indien de klok via een willekeurige polygoon van A naar B
wordt verplaatst en zelfs indien de punten A en B
samenvallen.
Als we aannemen dat het voor een polygoon bewezen resultaat
ook voor een continue, gebogen kromme geldt, dan leidt dat tot de volgende
stelling.
Indien zich in A twee gelijklopende klokken bevinden en als men
één van de klokken met constante snelheid langs een gesloten kromme verplaatst
tot hij weer in A is teruggekeerd, wat bijvoorbeeld t
seconde duurt, dan loopt de laatste klok bij zijn aankomst in A in
vergelijking tot de klok die in A was gebleven,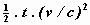 
seconde achter. Men kan daaruit concluderen dat een klok, waarvan de werking
berust op een onrust en die op de evenaar van de aarde is geplaatst, een heel
klein beetje langzamer moet lopen dan een identieke klok die zich aan de pool
bevindt en verder aan gelijke omstandigheden wordt blootgesteld.
